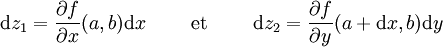- Differentielle
-
Différentielle
En analyse fonctionnelle et vectorielle, on appelle différentielle d'ordre 1 d'une fonction en un point a la partie linéaire de l'accroissement de cette fonction entre a et a + h lorsque h tend vers 0. Elle généralise le calcul de dérivées et de développements limités aux fonctions de plusieurs variables. Cette différentielle n'existe pas toujours, et une fonction possédant une différentielle est appelée une fonction différentiable. On peut ensuite calculer des différentielles d'ordre supérieur à 1.
On utilise la notation différentielle avec beaucoup d'efficacité dans le cadre du calcul d'approximations et du calcul de dérivées. Elle facilite la formule de la dérivée de la composée. Elle se révèle très pratique dans le changement de variable en calcul intégral.
Dans l'approche de Leibniz, la différentielle d'une fonction est son « accroissement infinitésimal », qui s'écrit comme une combinaison des accroissements infinitésimaux des différentes variables. Ainsi pour une fonction f des variables x et y, son accroissement infinitésimal df s'exprime sous la forme :
où
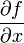 et
et 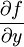 sont les dérivées partielles de f.
sont les dérivées partielles de f.Le calcul différentiel ainsi conçu, s'il était un outil de calcul efficace, manquait d'un fondement rigoureux, en particulier en ce qui concerne la notion de quantité infinitésimale. La notion moderne de différentielle est l'outil algébrique qui permet de passer des accroissements finis des variables δx,δy à l'accroissement de la fonction δf, en se limitant au premier ordre d'approximation. Mathématiquement, il n'est plus question de petite variation mais de calcul au premier ordre, dont la définition s'exprime sous forme d'une limite.
Il convient cependant de ne pas négliger la puissance d'évocation et l'efficacité dans les calculs du point de vue original de Leibniz. C'est ce qui explique qu'il reste massivement utilisé, notamment par les physiciens. En introduisant la notion avancée de calcul tensoriel sur les variétés, les mathématiciens ont pu assurer un statut précis aux notations différentielles de tous ordres.
Sommaire
Première approche
Fonction d'une seule variable
Le calcul différentiel, pour les fonctions d'une seule variable, se confond avec la dérivation. Soit f une fonction d'une variable réelle, à valeurs réelles ; on notera y = f(x) le résultat de l'application de f. Elle est dite dérivable lorsque
où
 est une fonction ayant une limite nulle en 0. On résume souvent cela par la notation (souvent dite notation de Landau)
est une fonction ayant une limite nulle en 0. On résume souvent cela par la notation (souvent dite notation de Landau)Intuitivement ce calcul de limite, qui porte le nom de développement limité à l'ordre 1 pour la fonction f en a, signifie qu'en première approximation, pour h proche de 0, l'expression f(a + h) est peu différente de l'expression
 . Notamment parmi les expressions de la forme α + βh, c'est celle-ci qui donne la meilleure approximation de f(a + h).
. Notamment parmi les expressions de la forme α + βh, c'est celle-ci qui donne la meilleure approximation de f(a + h).Introduction intuitive des notations du calcul infinitésimal
Dans de nombreuses applications, des notations parlantes sont employées pour décrire cette situation. On convient de noter le nombre h par dx pour indiquer qu'il représente une très petite variation de x par rapport à la valeur de référence a. On note dy la variation de l'image par rapport à la valeur de référence :
Le point de vue couramment adopté, abusif en toute rigueur, est que pour des variations suffisamment petites, on peut écrire dy = f'(a)dx. Cette présentation escamote en effet la nécessité d'utiliser un calcul de limite, car même pour des variations très petites, le terme d'erreur noté o(h) ci-dessus n'a pas de raison d'être nul. Mathématiquement parlant il serait plus juste de noter cela
Car les mathématiciens prouvent la formule exacte dy = f'(a)dx, en donnant aux notations dx et dy un sens précis qui n'est pas celui de petites variations et qui sera détaillé plus bas.
Fonction de deux variables
Soit une fonction f des deux variables x et y ; on notera z = f(x,y) le résultat de l'application de f.
Valeur attendue pour la différentielle
De nouveau la question posée peut être formulée ainsi : lorsque, par rapport à des valeurs de référence a et b, on augmente les variables x et y des quantités dx et dy, quel est l'effet (au premier ordre) sur la variable z ?
Les dérivées partielles permettent de répondre à la question lorsqu'une des deux variations est nulle. Ainsi, parce que c'est un simple calcul de dérivée de fonction d'une variable, il est possible d'écrire
et de même en inversant les rôles : si dx est nul, dz se calcule à l'aide de la deuxième dérivée partielle.
Il semblerait naturel que lorsqu'on augmente x et y respectivement des quantités dx et dy, l'augmentation totale soit obtenue en superposant les deux cas précédents
ce qu'en physique on énonce en général sous la forme : la différentielle totale est la somme des différentielles partielles.
- On écrira par exemple : si
 alors
alors 
De fait, cette formule sera vérifiée dans de très nombreux calculs explicites ; mais elle n'est pas vraie en toute généralité.
Le problème de la différentiabilité
Il faut détailler le raisonnement pour voir où il pèche : on peut faire subir d'abord une augmentation de dx à la seule variable x, ce qui la fait passer de la valeur a à a + dx, tandis que y reste égale à b. Puis, en maintenant x = a + dx constant, on fait passer y de b à b + dy. Les accroissements de z résultants sont donc plus précisément
et encore si cette deuxième quantité existe effectivement.
L'existence de dérivées partielles au seul point (a,b) est a priori insuffisant pour écrire une formule générale de calcul de dz. En revanche, si on suppose que les dérivées partielles sont définies et continues sur un voisinage de (a,b), on pourra effectivement affirmer que dz a la valeur attendue.
Définition de la différentielle
En termes généraux, la différentiabilité est l'existence d'un développement limité à l'ordre 1 en un point, et la différentielle est la partie d'ordre 1 (donc linéaire) exactement.
Pour une fonction réelle à deux variables
Étudions en premier lieu une fonction de deux variables, à valeurs réelles : on notera z = f(x,y). Cette fonction sera dite différentiable au point
 de coordonnées (x,y) s'il existe une formule de développement limité d'ordre 1 pour la fonction en ce point, c'est-à-dire
de coordonnées (x,y) s'il existe une formule de développement limité d'ordre 1 pour la fonction en ce point, c'est-à-direavec α et β des coefficients réels.
Si la fonction est différentiable, on montre que les coefficients α et β sont bien les dérivées partielles de f. On peut alors écrire
avec l'expression suivante qui est linéaire en

L'application linéaire L est appelée différentielle de f au point
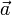 et notée
et notée  .
.On peut reprendre l'interprétation intuitive de L. Si les variables subissent une petite modification
 , l'effet sur la fonction est une modification
, l'effet sur la fonction est une modification  , à condition de s'empresser d'ajouter : du moins au premier ordre.
, à condition de s'empresser d'ajouter : du moins au premier ordre.Remarque : le calcul de
 peut aussi être présenté comme un calcul de produit scalaire avec le vecteur gradient de f.
peut aussi être présenté comme un calcul de produit scalaire avec le vecteur gradient de f.Généralisations en dimension finie
Cette première notion se généralise aux fonctions de
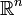 dans
dans  , en changeant simplement le nombre de variables, puis aux fonctions de
, en changeant simplement le nombre de variables, puis aux fonctions de 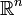 dans
dans  en admettant des coefficients vectoriels pour le développement limité. Une fonction
en admettant des coefficients vectoriels pour le développement limité. Une fonction  de
de 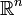 dans
dans  sera dite différentiable en
sera dite différentiable en 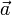 s'il existe un développement de la forme
s'il existe un développement de la formeavec
 qui désigne la norme du vecteur de composantes (h1,...,hn). De nouveau, si la fonction est différentiable, on montre que les coefficients
qui désigne la norme du vecteur de composantes (h1,...,hn). De nouveau, si la fonction est différentiable, on montre que les coefficients  apparaissant dans ce développement sont les dérivées partielles de
apparaissant dans ce développement sont les dérivées partielles de  . On notera donc
. On notera doncPour effectuer ce calcul il est judicieux d'introduire des représentations matricielles pour le vecteur
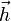 et l'application linéaire
et l'application linéaire  : c'est ce que l'on appelle la matrice jacobienne de l'application. C'est une matrice de dimension (n,p).
: c'est ce que l'on appelle la matrice jacobienne de l'application. C'est une matrice de dimension (n,p).Si la différentiabilité de la fonction assure l'existence de dérivées partielles, la réciproque est fausse : l'existence de dérivées partielles n'assure pas toujours la différentiabilité de la fonction, ni même sa continuité.
Il existe cependant un résultat positif : si les dérivées partielles de f existent et sont continues, alors f est différentiable.
Définition générale
Plus généralement, il est possible de définir la notion de différentiabilité et de différentielle sans avoir recours à des bases. Soient E et F deux espaces vectoriels normés, et f une application de E dans F. Soit a un point de E. On abandonne la notation des vecteurs par des flèches dans ce paragraphe.
On dit que f est différentiable en a si et seulement s’il existe une application linéaire continue L de E dans F telle que :
Dans ce cas, L est appelée différentielle de f en a et se note L = df(a).
Comme pour la continuité des applications linéaires, la différentiabilité dépend de la norme choisie. On retrouve la définition usuelle en dimension finie puisque toutes les applications linéaires sont continues, toutes les normes équivalentes.
Remarque : on peut remarquer le changement sémantique entre la première définition, celle de Leibniz – un accroissement très petit –, et celle formalisée de nos jours – une application linéaire. Ce changement est l'aboutissement d'un évolution de plus de trois siècles entre un idée intuitive du calcul infinitésimal et sa formalisation.
Différentielle d'ordre supérieur
Cas de la fonction réelle
Si y = f(x), si f est dérivable sur I, alors
 . Si de plus,
. Si de plus,  est dérivable, df est différentiable et
est dérivable, df est différentiable et . Cette quantité s'appelle la différentielle d'ordre 2 de f.
. Cette quantité s'appelle la différentielle d'ordre 2 de f.
Plus généralement, si f est n fois dérivable sur I, on appelle différentielle d'ordre n sur I, l'expression
Cas de la fonction réelle à deux variables
Si f est une fonction différentiable sur I (ouvert de
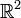 ), alors
), alors  , chacune des fonctions
, chacune des fonctions  et
et  est elle-même une fonction de
est elle-même une fonction de 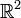 dans
dans  . Si elles sont différentiables de différentielle continue (c'est-à-dire C1) alors df est aussi différentiable et
. Si elles sont différentiables de différentielle continue (c'est-à-dire C1) alors df est aussi différentiable et .
.
Comme les différentielles sont continues, le théorème de Schwarz permet de dire que :
ce qui permet d'écrire la différentielle d'ordre 2 de f sous la forme suivante :
où
 devient un opérateur agissant sur f.
devient un opérateur agissant sur f.Plus généralement, si f est de classe Cn alors
Cas général
Voir aussi
- Portail des mathématiques
Catégories : Analyse à plusieurs variables | Analyse
Wikimedia Foundation. 2010.