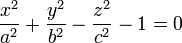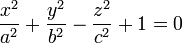Hyperboloide

Hyperboloide

Hyperboloïde

En mathématiques, un hyperboloïde est une surface du second degré de l'espace euclidien. Il fait donc partie des quadriques, avec pour caractéristique principale de posséder un centre de symétrie et de s'étendre à l'infini.

Les sections non triviales d'un hyperboloïde avec un plan sont des paraboles, des ellipses ou des hyperboles. On distingue deux types d'hyperboloïdes, connexes ou non, chaque partie connexe s'appelant une nappe.

Le cône peut être vu comme une forme dégénérée d'hyperboloïde.

Hyperboloïde à une nappe

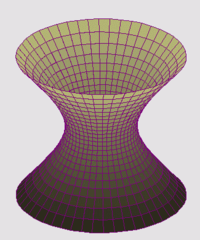
Hyperboloïde à une nappe

Dans un repère bien choisi, son équation cartésienne est de la forme

{x^2 \over a^2} + {y^2 \over b^2} - {z^2 \over c^2}-1=0

Le cas a = b fournit, en repère orthonormé, le cas particulier d'un hyperboloïde de révolution. L'axe de rotation doit être l'axe non transverse pour que la surface ne possède qu'une nappe. Les sections avec un plan perpendiculaire à l'axe de rotation sont alors des cercles :


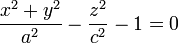\frac{x^2+y^2}{a^2}-\frac{z^2}{c^2}-1=0 (une nappe)


Le dessin ci-contre utilise une hyperbole équilatère, alors a = b = c.

Un château d'eau de forme hyperboloïde - on aperçoit les renforcements rectilignes.

On peut aussi générer cette surface par rotation d'une droite oblique autour de l'axe. Cette propriété justifie que l'hyperboloïde à une nappe est une surface réglée non développable. Cela permet, en pratique, de réaliser le coffrage de construction de certains châteaux d'eau et de certaines tours de refroidissement de centrales à partir d'éléments rectilignes, ce qui leur assure une certaine stabilité.

Hyperboloïde à deux nappes

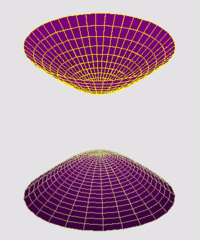
Hyperboloïde à deux nappes

Dans un repère bien choisi, son équation cartésienne est de la forme

{x^2 \over a^2} + {y^2 \over b^2} - {z^2 \over c^2}+1=0

C'est la seule quadrique non connexe.


Le cas a = b fournit, en repère orthonormé, le cas particulier d'un hyperboloïde de révolution. L'axe de rotation doit être l'axe focal pour que la surface possède deux nappes. Les sections avec un plan perpendiculaire à l'axe de rotation sont alors des cercles soit :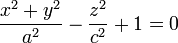


\frac{x^2+y^2}{a^2}-\frac{z^2}{c^2}+1=0 (deux nappes)


Le dessin ci-contre utilise une hyperbole équilatère, alors a = b = c.


Articles connexes

Commons-logo.svg
  • Portail de la géométrie Portail de la géométrie
Ce document provient de « Hyperbolo%C3%AFde ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Hyperboloide de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

  • hyperboloïde — [ ipɛrbɔlɔid ] adj. et n. m. • 1765; de hyperbole et oïde ♦ Didact. 1 ♦ Rare En forme d hyperbole. 2 ♦ N. m. Math. Quadrique à centre dont les sections planes sont des hyperboles. Hyperboloïde de révolution. ● hyperboloïde nom masculin Quadrique… …   Encyclopédie Universelle

  • Hyperboloide — Hyperboloide, nicht geschlossene Curven 2. Grades, in hyperbolische und elliptische eingetheilt …   Herders Conversations-Lexikon

  • Hyperboloïde — En mathématiques, et plus précisément en géométrie, un hyperboloïde est une surface du second degré de l espace euclidien. Il fait donc partie des quadriques, avec pour caractéristique principale de posséder un centre de symétrie et de s étendre… …   Wikipédia en Français

  • hyperboloïde — (i pèr bo lo i d ) adj. Terme de géométrie. Qui se rapproche de l hyperbole. Courbes hyperboloïdes.    S. m. Solide produit par la révolution d une hyperbole. ÉTYMOLOGIE    Hyperbole, et terme grec signifiant forme. SUPPLÉMENT AU DICTIONNAIRE… …   Dictionnaire de la Langue Française d'Émile Littré

  • hyperboloïde — hiperboloidas statusas T sritis fizika atitikmenys: angl. hyperboloid vok. Hyperboloid, m rus. гиперболоид, m pranc. hyperboloïde, m …   Fizikos terminų žodynas

  • Hyperboloïde de révolution — ● Hyperboloïde de révolution hyperboloïde engendré par la rotation d une hyperbole autour d un de ses axes de symétrie …   Encyclopédie Universelle

  • Structure hyperboloïde — Sur les autres projets Wikimedia : « Structure hyperboloïde », sur Wikimedia Commons (ressources multimédia) La première structure hyperboloïde au monde la tour de treillage de claire voie d acier située actuellement à Polibino… …   Wikipédia en Français

  • Structures de hyperboloide — Structure hyperboloïde La première structure hyperboloïde par Vladimir Choukhov, Nijni Novgorod, 1896 …   Wikipédia en Français

  • Structures de hyperboloïde — Structure hyperboloïde La première structure hyperboloïde par Vladimir Choukhov, Nijni Novgorod, 1896 …   Wikipédia en Français

  • Modèle de l'hyperboloïde — En géométrie, le modèle de l hyperboloïde, également dénommé modèle de Minkowski ou modèle de Lorentz (d après les noms de Hermann Minkowski et Hendrik Lorentz), est un modèle de géométrie hyperbolique dans un espace de Minkowski de dimension n.… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”