- Théorie des équations (histoire des sciences)
-
 Pour les articles homonymes, voir Théorie des équations.
Pour les articles homonymes, voir Théorie des équations. Évariste Galois offre une condition nécessaire et suffisante à la résolution d'une équation polynomiale par l’algèbre. Il répond ainsi à une question centrale de la théorie, ouverte depuis des millénaires. Sa méthode fournit des résultats novateurs, à l’origine de nouvelles branches de l’algèbre, qui dépassent le cadre de la théorie des équations.
Évariste Galois offre une condition nécessaire et suffisante à la résolution d'une équation polynomiale par l’algèbre. Il répond ainsi à une question centrale de la théorie, ouverte depuis des millénaires. Sa méthode fournit des résultats novateurs, à l’origine de nouvelles branches de l’algèbre, qui dépassent le cadre de la théorie des équations.
La théorie des équations est un ensemble de travaux ayant pour objectif premier la résolution d’équations polynomiales[Note 1] ou équivalentes[Note 2]. Une telle équation s’écrit de la manière suivante :

où X désigne l’inconnue.
La « théorie des équations » est une expression utilisée en histoire des sciences[ADD 1].
L’étude de ce type de questions remonte aux premiers textes mathématiques connus[Note 3]. Une première approche permet de résoudre l’équation dans le cas où le degré du polynôme est strictement plus petit que cinq. C'est durant la Renaissance et avec l'étude des équations cubiques que de nouveaux nombres sont utilisés[Note 4]. Ils sont qualifiés initialement d’imaginaires puis de nombres complexes. Ce n'est que plus tard que ceux-ci interviennent comme solutions d’équations de degré deux.
À partir de l'époque moderne, le polynôme est aussi considéré comme une fonction. Cette approche offre des méthodes pour déterminer le nombre de racines réelles, pour localiser les racines (c’est-à-dire trouver des régions où elles se trouvent) et pour fournir des méthodes d’approximations aussi précises que souhaité. L’un de ses achèvements est le théorème de d'Alembert-Gauss, qui indique qu’une fonction polynomiale non constante admet au moins une racine dans les nombres complexes.
Un point de vue du XIXe siècle consiste à étudier le plus petit ensemble de nombres, stable pour les quatre opérations et qui contienne à la fois coefficients et racines d'une équation donnée. Cette approche entre dans la théorie dite de Galois. Elle offre une condition nécessaire et suffisante pour savoir si une équation polynomiale se résout par les techniques décrites par la première approche, dans le cas contraire l’on doit se limiter à des approximations issues de l’analyse. Jusqu’au XIXe siècle, la théorie des équations se confond avec l’algèbre. Puis, à la suite de la théorie de Galois principalement, l’algèbre s’élargit pour prendre en compte de nouvelles questions. Cette théorie est à l’origine de vastes domaines mathématiques, comme la théorie des groupes, celle des anneaux ou encore la géométrie algébrique.
- Remarque : Quand on ne précise pas, le terme de théorie des équations désigne généralement[Note 5] les équations polynomiales[1]. En revanche, il existe de nombreuses équations qui, sans être algébriques, font néanmoins l’objet d’une théorie. L’usage veut alors que l’on précise la nature de l’équation, comme dans l’expression théorie des équations différentielles[2]. Il n’existe pas de théorie unique s’appliquant à tout type d’équations, elles forment pour cela un ensemble trop disparate.
Sommaire
Origines
Avant la théorie
Article détaillé : Inconnue (mathématiques). Le livre Arithmetica de Diophante est le premier à décrire l'inconnue au sens mathématique du terme.
Le livre Arithmetica de Diophante est le premier à décrire l'inconnue au sens mathématique du terme.
Aussi loin que remontent les textes connus en mathématiques, on y trouve des questions qui s'expriment, en langage contemporain, sous forme d’équations algébriques. On lit, dans un papyrus de l’Égypte ancienne : « Quand le scribe te dit de quoi 10 est les 2/3 et le 1/10 ? »[ADD 2] ce qui se traduit par 2/3x + 1/10x = 10. Des problèmes du second degré sont particulièrement étudiés par les Babyloniens. Leur langage est géométrique, la valeur recherchée, notée ici x, est appelée coté et x2 carré, mais leur formulation est souvent purement algébrique. On peut lire, sur une tablette d’argile : « J’ai additionné 7 fois le côté de mon carré et 11 fois la surface : 6 15 »[3], pour décrire (en numérotation sexagésimale utilisée par les Babyloniens) l’équation 11x2 + 7x = 6x60 + 15= 375. Le sens géométrique de la somme d’une aire et d’une longueur est ambiguë, cependant aucun commentaire n’étaye une interprétation purement algébrique de la question (des nombres multipliés et additionnés). Aucun outil algébrique n’est développé, il n’existe pas d'inconnue que l’on peut déterminer à l’aide d'une méthode calculatoire. Les Égyptiens résolvent l’équation du premier degré par essais successifs, à l’aide de la méthode de la fausse position et les Babyloniens disposent d’algorithmes sans autre justification qu'empirique, c’est-à-dire qu’à la fin la valeur trouvée est bien la solution recherchée.
La première étape qui approche de l’ébauche d’une véritable théorie demande plus de deux millénaires. Elle est franchie indépendamment par trois cultures mathématiques : la Grèce, la civilisation arabe et celle des Indes. Diophante, un mathématicien du IIIe siècle, formalise l'arithme, une lettre qu’il définit[4] par : « Le nombre qui possède une quantité indéterminée d’unités s’appelle l’arithme, et sa marque distinctive est σ. » L’arithme s’additionne et se multiplie : « l’inverse de l’arithme multiplié par le bicarré de l’arithme donne le cube de l’arithme[5]. » ce qui signifie en langage moderne que x divise x4 et que le résultat est égal à x3. Cette démarche permet une véritable formulation mathématique de l’équation et surtout, un mode de résolution. Avant que Diophante ne soit traduit en arabe[ADD 3], Al-Khawarizmi, un mathématicien d’origine perse, développe au VIIIe siècle une idée analogue. Son inconnue s’appelle le say’[6]. Une fois encore, le nouveau formalisme offre un moyen de résolution de l’équation. R. Rashed indique : « [Avec Al-Khwarizmi] la notion de base c’est la notion d’équation, qui peut couvrir une classe infinie de problèmes, géométriques ou arithmétiques : l’unité n’est plus l’objet mais l’opération même[7]. » La même idée est encore présente chez le mathématicien indien Bhāskara II dans son texte intitulé Bījagaṇita[8].
Les différentes méthodes de résolution des problèmes des premier et second degrés, avec et sans le formalisme de l’équation, sont présentées dans l’article détaillé.
Algèbre arabe
 Les polynômes d’al-Samaw'al représentés par un tableau préfigurent une conception purement abstraite de l’algèbre.
Les polynômes d’al-Samaw'al représentés par un tableau préfigurent une conception purement abstraite de l’algèbre.
Le mathématicien Al-Khawarizmi est souvent considéré comme fondateur de la branche des mathématiques appelée algèbre. En termes d’étymologie, le titre de son traité sur les équations : Kitâb al-jabr wa al-muqâbala utilise le terme al-jabr, devenu algèbre. En arabe, al-jabr vise « à transformer une soustraction dans un membre en une addition dans l’autre membre »[9] dans l’objectif d’obtenir uniquement des coefficients positifs. Par exemple[9] : 2x2 + 100 - 20x = 58 devient en suivant ce procédé : 2x2 + 100 = 58 + 20x. A. Dahan-Dalmedico et J. Peiffer précisent que le travail d’Al-Khawarizmi est : « l’acte de naissance d’une théorie des équations quadratiques, dans l’ensemble des nombres positifs (presque toujours rationnels), théorie qui comporte encore quelques lacunes »[ADD 4]. Ce n’est pas uniquement l’étymologie qui justifie cette attribution à Al-Khawarizmi : en effet, celui-ci s’intéresse à toutes les équations du second degré, tandis que Diophante ne cherche à résoudre que quelques cas particuliers, à solutions entières ou rationnelles. Al-Khawarizmi a une démarche plus systématique : l’objet de son traité est d’offrir une méthode permettant de trouver à coup sûr, s'il en existe, une solution de l’équation.
Les progrès sur la théorie des équations ne s’arrêtent pas à Al-Khawarizmi. Il est à l’origine d’une école mathématique qui se développe sur plusieurs siècles. Son disciple Abu Kamil dissipe une première appréhension. À l’origine, les équations étudiées sont presque toujours à coefficients rationnels, Abu Kamil généralise l’étude aux coefficients irrationnels[ADD 5]. La conception initiale du nombre chez les Arabes est héritée des Grecs et se limite aux fractions. Les grandeurs incommensurables, qui correspondent à nos irrationnels, sont des proportions entre longueurs, mais ne possèdent pas le statut de nombre. Al-Khawarizmi les appelle gidr asamm, qui signifie racine muette ou aveugle[ADD 4]. Deux siècles plus tard, pour les mathématiciens comme Omar Khayyam, les fractions ou les proportions incommensurables sont traitées dans les calculs de la même manière, les deux concepts sont appelés al-adad, qui signifie nombre (les rationnels sont désignés par le terme al-adad al muntiqa et les irrationnels par al-adad al-summa), la différence n’étant plus que philosophique[ADD 6].
Des outils spécifiques sont développés pour permettre le calcul plus aisé des multiplications de polynômes. Al-Samaw'al les note sous la forme d'un tableau préfigurant une représentation proche du concept moderne de polynôme formel[Note 6].
Géométrie au service de l’algèbre
Article détaillé : Algèbre géométrique. Les gnomons et la géométrie d’Euclide sont le moteur de la résolution des équations algébriques pendant plusieurs siècles.
Les gnomons et la géométrie d’Euclide sont le moteur de la résolution des équations algébriques pendant plusieurs siècles.
La géométrie, et particulièrement celle des Éléments d'Euclide, joue un rôle fondamental dans cette algèbre naissante. Dans le cas d’une équation du second degré et après division par le coefficient du monôme dominant, le monôme du second degré peut être vu comme l’aire d’un carré dont le côté est l’inconnue que l’on recherche. Dans le cas de l’équation du premier degré, on interprète le terme du premier degré comme l’aire d’un rectangle dont les dimensions sont l’inconnue et le coefficient du monôme ; la constante est interprétée comme l’aire d’un carré parfaitement déterminé. Cette approche permet déjà à Euclide de résoudre des problèmes des premier et second degrés[Note 7]. L’angle d’analyse des Arabes est différent puisqu’ils cherchent à résoudre une équation, dans ce cas particulier, du second degré. Cependant le cœur de la démonstration est le même : une analyse d’une configuration géométrique, construite sur la base d’un gnomon. De manière méthodique, l’étude du gnomon permet d’établir les trois identités remarquables source de résolution des équations du second degré.
L’approche utilisée pour étendre la théorie naissante des équations à l’équation cubique est tout aussi géométrique, mais cette fois avec des outils un peu différents. Al-Khayyām remarque qu’il est possible d’interpréter la racine de l’équation cubique comme l’abscisse de l’intersection d’un cercle et d’une parabole[Note 8], ce qui montre déjà l’usage de ce que l’on appellera plus tard un repère cartésien et permet de remarquer l’existence possible de plusieurs solutions[ADD 7]. Deux siècles plus tard, profitant des progrès tant algébriques que géométriques, Nasir ad-Din at-Tusi développe plusieurs outils dans le cadre de l’équation cubique. Le discriminant lui permet de connaître l’existence de racines positives dans certaines situations[ADD 8], la dérivation formelle lui permet de localiser les racines et une méthode numérique, variante de celle maintenant dite de Ruffini-Horner, permet d'approcher la racine avec la précision souhaitée[10].
Les méthodes mathématiques utilisées, ainsi que cette branche de l'histoire des mathématiques, sont développées dans l’article détaillé.
Diffusion en Europe
Article détaillé : Équation cubique. Girolamo Cardano généralise la formule de Tartaglia en lui adjoignant des nombres imaginaires pour résoudre des cas qualifiés alors d’irréductibles.
Girolamo Cardano généralise la formule de Tartaglia en lui adjoignant des nombres imaginaires pour résoudre des cas qualifiés alors d’irréductibles.
À travers les textes de Fibonacci ou encore de Luca Pacioli, l’Italie a accès, au début du XVIe siècle, à l’essentiel du savoir arabe. Les mathématiciens d’alors se passionnent pour l’algèbre et, surtout, pour un problème laissé ouvert : trouver une méthode générale et exacte de résolution de l’équation cubique. Par exacte, on entend une forme différente d’une suite qui converge vers la racine. Ces mathématiciens recherchent une expression analogue à celle d’Al-Khawarizmi pour le second degré qui, à l’aide de racines carrées ou cubiques, donnerait la solution.
L’âpre compétition qui règne entre les différents mathématiciens stimule les candidats et pousse à l’émergence d’idées nouvelles. Scipione del Ferro trouve comme formule de résolution de l’équation X3 + aX = b :
![x= \sqrt[3] {\frac b2 + \sqrt {\left(\frac b2\right)^2 + \left(\frac a3\right)^3}} + \sqrt[3] {\frac b2 - \sqrt {\left(\frac b2\right)^2 + \left(\frac a3\right)^3}}](3/16355c2c9eb2d8ec58af9a6535fb73b4.png)
A. Dahan-Dalmedico et J. Peiffer précisent : « Elle devait [...] provoquer de grands progrès dans la théorie des équations [...] »[ADD 9]. La formule avait à l’époque de quoi susciter l’étonnement. Un calcul algébrique est encore justifié par un support géométrique. Un nombre tire sa justification d’une longueur, d’une aire ou d’un volume. Le signe - n’a de sens que si une longueur est soustraite à une plus grande. Dans la solution que propose del Ferro, on retranche une longueur à une autre longueur plus petite[Note 9]. À cette époque, l’enjeu est de relever des défis, c’est-à-dire de résoudre des équations particulières[11], la rigueur de la méthode importe peu, tant qu’il est finalement possible de vérifier le résultat en remplaçant x dans l’équation par la solution présumée.
Une question reste ouverte : comment résoudre l’équation X3 + a = bX, si 4b3 > 27a2 ? Cette fois-ci, la méthode semble impraticable car la grandeur négative qui apparaît devrait correspondre à la surface d’un carré (au sens géométrique du terme). Tartaglia, un des spécialistes de l’époque en la matière, qualifie l’équation d’irréductible. C’est finalement Cardano qui trouve la solution : il suffit de ne pas arrêter les calculs. Ces étranges termes finissent par disparaître[12] ; par exemple en appliquant des identités remarquables comme[ADD 10] :

Une nouvelle étape est franchie. Si la signification précise de l’expression √-1 reste mystérieuse, l’idée de faire appel à un ensemble de nombres plus grand pour résoudre une question en théorie des équations est découverte. Un élève de Cardano, Ludovico Ferrari résout l’équation quartique, en 1540[13]. Bombelli propose un formalisme autorisant l’existence de nombres négatifs et imaginaires. Son influence, attestée par les commentaires de Stévin ou la correspondance entre Leibnitz et Huygens, est durable[ADD 11].
L’article Méthode de Cardan présente la solution, en termes contemporains, de l’équation cubique, et celui intitulé Méthode de Ferrari celle du quatrième degré.
Nouveau départ
Viète, Fermat et Descartes
 En découvrant le calcul littéral, François Viète trouve un langage formel donnant à l’algèbre son autonomie par rapport à la géométrie.
En découvrant le calcul littéral, François Viète trouve un langage formel donnant à l’algèbre son autonomie par rapport à la géométrie.
Le début d'une véritable théorie des équations[14] est généralement attribué à Viète, mathématicien français de la fin du XVIe siècle. S’il refuse encore de considérer les avancées de Bombelli, c’est-à-dire les nombres négatifs ou imaginaires, il réalise néanmoins trois avancées majeures.
La plus célèbre est probablement celle qu’il appelle la logique spécieuse et que l’on qualifie maintenant de calcul littéral. Viète réunit deux usages des lettres en mathématiques[ADD 12]. Celui de l'algèbre se répand et se perfectionne en Europe au cours du XVIe siècle[Note 10], mais apparaissait déjà chez Diophante : une lettre s’additionne ou se multiplie et joue le rôle d’inconnue dans une équation. Celui de la géométrie est courant dès l'Antiquité : une lettre désigne une grandeur ou un objet non spécifié, point, droite, distance entre deux points sur une figure … Les principes généraux de résolution des équations ne peuvent être établis qu'à l’aide de la géométrie, comme l’usage de gnomons pour les identités remarquables, puis illustrés par des exemples d’équations polynomiales aux coefficients numériques, que Viète considère comme appartenant à la logique numéreuse. Viète introduit une deuxième catégorie de lettres pour les coefficients. Ceux-ci sont aussi des valeurs considérées comme fixées, même si on ne les connaît pas : c'est ce qu'on appelle maintenant un paramètre. En transportant une ancienne habitude géométrique à l’algèbre, Viète crée la logique spécieuse. Cette nouvelle approche revient à considérer une équation comme une expression du type : aX2 + bX = c. Réussir à résoudre cette équation c’est être capable de résoudre toutes les équations du second degré, un unique cas général de logique spécieuse permet de traiter une infinité de cas particuliers issus de la logique numéreuse.
À ce premier apport, Viète ajoute le développement d’un langage symbolique permettant d’exprimer plus simplement une expression polynomiale. Les idées de Viète permettent une expression plus limpide que celle de ses prédécesseurs. Son vocabulaire est toujours en partie d’actualité : on lui doit le terme de coefficient[ADD 13] ainsi que celui de polynôme[15].
Ce formalisme permet d’exprimer les premiers résultats généraux, au sens ou ils sont indépendants du degré du polynôme, comme la relation entre les coefficients et les racines d’un polynôme.
Le système de notations de Viète est repris par Fermat et Descartes pour, d’après Nicolas Bourbaki, devenir « à peu de choses près, celui que nous utilisons aujourd’hui[16]. » Ces travaux permettent un renversement de la hiérarchie mathématique. Jusqu’à Viète, la théorie des équations est nécessairement une émanation de la géométrie. L’unique méthode générique de démonstration se fonde sur les Éléments d’Euclide et les calculs-clés, comme les identités remarquables, sont établis à l’aide de considérations géométriques. Le calcul littéral permet d’affranchir l’algèbre de ces contraintes. Pour Descartes, l’algèbre, additionnée de l’usage d’un repère cartésien, devient une machine à démontrer des théorèmes géométriques. Elle est une « extension de la logique, dénuée de toute signification par elle-même, mais indispensable pour le maniement des quantités, et, en un sens, plus fondamentale même que la géométrie[ADD 14]. »
Calcul infinitésimal
 La méthode de Newton permet d’approximer aussi précisément que souhaité une racine d’un polynôme.
La méthode de Newton permet d’approximer aussi précisément que souhaité une racine d’un polynôme.
La deuxième moitié du XVIIe siècle est l’époque d’un séisme appelé calcul infinitésimal. L’étude des trajectoires et des mouvements, issue de la physique, est à l’origine de nouvelles idées[ADD 15]. Pour cette étude, Isaac Newton cherche à modéliser l’idée de variable à l’aide du concept de temps, qu’il appelle fluente : « J'appellerai quantité fluente, ou simplement fluente, ces quantités que je considère comme augmentées graduellement et indéfiniment, et je les représenterai par les dernières lettres de l’alphabet v, x, y et z »[ADD 16].
Vu sous l’angle de la théorie des équations, cela revient à remplacer le X des formules utilisées depuis Diophante, par un x qui devient une quantité qui varie de moins à plus l’infini. Le polynôme devient une fonction et à ce titre jouit de nouvelles propriétés. Les outils associés au calcul infinitésimal sont la limite, la dérivée ou encore l’intégrale. En 1691, Michel Rolle les utilise pour établir un théorème, indiquant que si a et b sont deux racines d’un polynôme P non constamment nul, il existe une valeur c comprise dans l’intervalle ]a, b[racine du polynôme dérivée de P[17], retrouvant un résultat[18] de Bhaskara II et Sharaf al-Dîn al-Tûsîau du XIIe siècle. Une autre application est une découverte de Newton pour le calcul des racines, appelée méthode de Newton[H 1]. Elle consiste à choisir initialement une valeur, à calculer la tangente du polynôme en cette valeur, à trouver la racine de la tangente et à réitérer.
Si ces résultats apportent des éléments nouveaux à la théorie des équations, ils n’en font pas partie au sens propre. Newton développe sa méthode pour les polynômes, mais elle n’est en rien spécifique à ceux-ci et permet d’approximer un zéro d’une fonction dérivable quelconque, ce dont Newton prend conscience puisqu’il applique ensuite sa méthode à des fonctions non polynomiales. Le théorème de Rolle est maintenant généralisé à toute fonction dérivable, même si la démonstration de ce résultat date de 1860[H 2]. D’autres résultats de même nature, comme la méthode de Ruffini-Horner pour approximer une racine ou le théorème de Sturm pour localiser la présence d’une solution dans un intervalle, sont mis au point durant le XIXe siècle.
Imaginaires et nombres complexes
 Les travaux de Leonhard Euler sont à l’origine d’une meilleure compréhension des nombres complexes, indispensable à la théorie des équations.
Les travaux de Leonhard Euler sont à l’origine d’une meilleure compréhension des nombres complexes, indispensable à la théorie des équations.
Les nombres imaginaires sont nés dans une ambiguïté que le calcul infinitésimal finit par dissiper. Pour Bombelli, un nombre imaginaire est une longueur géométrique à laquelle on a ajouté l’un des quatre signes possibles : le plus des vraies longueurs, le moins, ainsi que deux autres qu’il appelle piu di meno et meno di meno qui correspondent avec nos notations à i et -i[19]. Il existe une autre définition, plus générale mais plus vague, qui nous vient de Descartes. Il utilise pour la première fois le terme imaginaire en 1637. Pour exprimer les relations entre les coefficients et les racines, mises en évidence par Viète, il est nécessaire de faire parfois appel à des nombres impossibles soit parce qu’ils sont «moindres que rien» ce qui ne fait pas sens pour une longueur, soit parce qu’ils sont impossibles. Ces racines doivent alors être imaginées, elles sont « [...] quelquefois seulement imaginaires c’est-à-dire que l’on peut toujours en imaginer autant que j'ai dit en chaque équation, mais qu’il n’y a quelquefois aucune quantité qui corresponde à celle qu’on imagine »[H 3]. Ces deux définitions ne semblent pas équivalentes. Dans un cas, les nombres imaginaires sont définis comme des complexes de la forme a + i.b, dans l’autre, un nombre imaginaire est n’importe quoi qui pourrait servir aux calculs intermédiaires d’une équation algébrique. A. Dahan-Dalmedico et J. Peiffer précisent décrivent ainsi cette double définition : « Dès son origine, une ambiguïté préside à l’apparition de ce terme imaginaire : entre d’une part l’acception idéale de Descartes ou même de Girard et, d’autre part, les nombres de la forme a + b√-1, avec a, b réels, qui interviennent dans les résolutions des équations de bas degré[ADD 17] ».
Le calcul infinitésimal incite au choix d’une définition précise et permet de résoudre les paradoxes apparents de ces étranges nombres. La racine carrée possède une propriété algébrique, si a et b sont deux réels positifs, √a.√b = √a.b, d’où un premier paradoxe[Note 11] :

À travers des développements en série, Leibniz parvient à justifier des égalités de Bombelli comme[ADD 18] :
![\sqrt[3]{2+ \sqrt {-121}}+\sqrt[3]{2- \sqrt {-121}} = 4](2/9422499ef98c2f6142bddab1b6396728.png)
Les travaux de De Moivre mettent en évidence une correspondance entre les imaginaires de Bombelli et la trigonométrie[Note 12]. La formule d'Euler eiπ + 1 = 0 donne leurs lettres de noblesses aux nombres complexes de la forme a + i.b. Tobias Dantzig remarque que cette formule contient : « les symboles les plus importants : union mystérieuse dans laquelle l’arithmétique est représentée par 0 et 1, l’algèbre par √-1, la géométrie par π et l’analyse par e[ADD 19]. » La logique de Bombelli est définitivement adoptée.
Si ces travaux ne se rattachent pas à l'algèbre ou à la théorie des équations, ils sont néanmoins indispensables pour comprendre son histoire et son contenu.
Théorème fondamental de l’algèbre
Article détaillé : Théorème de d'Alembert-Gauss. Jean le Rond d’Alembert est le premier à ressentir la nécessité de démontrer le théorème fondamental de l’algèbre.
Jean le Rond d’Alembert est le premier à ressentir la nécessité de démontrer le théorème fondamental de l’algèbre.
Le récent statut acquis par ces nombres imaginaires impose la démonstration d’un théorème : Tout polynôme non constant admet au moins une racine complexe. Il est alors entendu que les coefficients sont des nombres réels. C’est Jean le Rond d’Alembert qui en exprime la première fois le besoin en 1746[20]. Sa motivation n’est en rien algébrique, il souhaite intégrer des fonctions rationnelles et utilise pour cela une décomposition en éléments simples. Sa démonstration est issue de ses préoccupations, elle est purement analytique.
La question est immédiatement considérée comme importante, et ce résultat prend le nom de théorème fondamental de l’algèbre. Le terme est cohérent car l’algèbre désigne, à cette époque, la théorie des équations. Mais la preuve de d’Alembert ne séduit pas. Tout d’abord, elle suppose connus deux résultats, l’existence d’un minimum pour une fonction continue définie sur un compact ; ensuite un théorème de convergence de série, maintenant appelé théorème de Puiseux. L’absence de techniques topologiques et de connaissance sur la convergence rend à l’époque impossible une démonstration complète. Ensuite, l’usage exclusif de l’analyse n’apparaît pas comme la méthode la plus adéquate pour démontrer le résultat fondamental de la théorie des équations[20].
Euler reprend la question sous un angle algébrique, héritage d’al-Khawarizmi et de Viète. Son objectif est de montrer que les racines, au sens de Descartes, sont bien des nombres complexes au sens de Bombelli. Dans le cas du degré 4, sa démonstration est rigoureuse mais inutile, les formules de Ferrari établissant déjà le résultat. Pour les autres cas, la démonstration n’est qu’esquissée[H 4]. Lagrange comble les lacunes en 1771[21].
Cette approche algébrique ne convainc pas Gauss qui indique : « l’hypothèse de base de la démonstration est que toute équation possède effectivement n racines possibles ou impossibles. Si l’on entend par possibles réels et par impossibles, complexes, cet axiome est inadmissible puisque c’est justement ce qu’il s’agit de démontrer. Mais si l’on entend par possibles les quantités réelles et complexes et par impossibles tout ce qui manque pour qu’on ait exactement n racines, cet axiome est acceptable. Impossible signifie alors quantité qui n’existe pas dans tout le domaine des grandeurs[ADD 20]. » Rien ne permet effectivement encore de donner un sens comme le fait Descartes aux racines, qui sont pourtant utilisées dans les calculs de Lagrange.
La première démonstration de Gauss est construite sur le canevas de d’Alembert, mais la compréhension des fonctions continues est encore trop faible pour permette de conclure. Les travaux de Bolzano finissent par permettre à Jean-Robert Argand de rédiger la première démonstration solide, encore sur les idées de d’Alembert[21]. Gauss trouve une preuve un peu plus tard, cette fois ci sur le canevas d’Euler et de Lagrange. Sa compréhension des polynômes formels lui permet de trouver un contournement[22]. Comme toutes les preuves algébriques du théorème, elle contient une partie analytique, à savoir l’existence d’une racine si le degré du polynôme est impair.
L’article détaillé relate plus précisément cette partie de l’histoire et propose diverses démonstrations du théorème.
Vers le théorème d'Abel
Premières tentatives
Article détaillé : Méthode de Tschirnhaus.Si la découverte du calcul infinitésimal permet quelques percées, celles-ci ne sont guère algébriques, et à ce titre n’entrent que partiellement dans la théorie des équations. Les mathématiciens , forts des succès concernant les équations de degré inférieur à quatre, se sont efforcés de trouver des formules analogues à celles d’al-Khawarizmi, Cardano ou Ferrari, mais cette fois pour un degré quelconque. Plusieurs tentatives, émanant de Tschirnhaus (un ami de Leibniz) puis d'Euler et enfin de Bézout, se soldent par des échecs.
Les canevas sont similaires, l’objectif est de ramener une équation de degré n à une forme canonique Xn - c = 0. À partir de cette forme canonique, l’équation n’est pas encore complètement résolue mais les travaux de Moivre en trigonométrie permettent d'écrire une solution x k, si c est positif :
![x_k = \sqrt[n]{c} \left( \cos \frac {2k\pi}{n} + i\sin \frac {2k\pi}{n}\right)](9/619e2d817a74abe662d2fcc5735e8ed5.png)
Pour cela, la méthode consiste à passer d’une équation à une inconnue P(X) = 0 à deux équations à deux inconnues en ajoutant la suivante : Q(X) - Y = 0. En choisissant habilement le polynôme Q, serait-il possible d’annuler les coefficients intermédiaires ? Pour n égal à 2, 3 ou même 4, cette méthode revient à résoudre une équation d’un degré inférieur, que l’on résout avec les méthodes précédentes. Mais avec n égale 5, l’équation à résoudre est de degré 120, et si l’on peut ramener son degré à 24 par d’autres artifices, la méthode n’est guère concluante.
Le point noir de la théorie reste la résolution effective de l’équation polynomiale[ADD 21].
Vandermonde et l’équation cyclotomique
Article détaillé : Polynôme cyclotomique.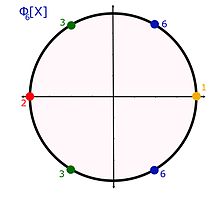 Les racines du polynôme cyclotomique sont régulièrement espacées sur le cercle trigonométrique complexe.
Les racines du polynôme cyclotomique sont régulièrement espacées sur le cercle trigonométrique complexe.
En 1771, Alexandre-Théophile Vandermonde apporte du nouveau sur ce délicat point noir[H 5]. Son ambition est plus modeste que celle de ses prédécesseurs. Il ne cherche plus à résoudre l’équation algébrique dans son intégralité, mais uniquement celle que les tentatives précédentes recherchaient comme point d’arrivée, à savoir Xn - c = 0. Comme le passage du coefficient 1 au coefficient c est trivial, il se limite à l’équation Xn - 1 = 0, dite cyclotomique[Note 13]. La valeur n peut être choisie parmi les nombres premiers, la résolution de ce cas particulier permet d’en déduire les solutions dans le cas général.
Une expression trigonométrique de la solution est connue, ce qui assure que les n racines de l’équation sont bien complexes et dans ce cas particulier, le théorème fondamental de l’algèbre est déjà établi. Il reste encore à trouver une formule algébrique capable de les exprimer. Par formule algébrique, on entend une expression contenant des nombres rationnels, l’unité imaginaire i, les quatre opérations et des fonctions racines nièmes. Le terme consacré est résolution par radicaux de l’équation algébrique.
La méthode de Vandermonde consiste à faire usage de polynômes en plusieurs indéterminées, et particulièrement des polynômes symétriques, c’est-à-dire ceux qui sont invariants par toute permutation des indéterminées. La relation entre les coefficients et les racines peut se lire comme le fait que n polynômes symétriques à n indéterminées ont une image connue du n-uplet des racines, ces images sont les coefficients du polynôme. Ce résultat est une reformulation d’une remarque de Viète. L’intérêt est que ces n polynômes symétriques génèrent l’intégralité des polynômes symétriques. En plus les images sont particulièrement simples pour le polynôme cyclotomique, elles sont toutes nulles, à l’exception de celle associée au polynôme X1...Xn, qui vaut ±1 selon la parité de n. Enfin, si les racines sont notées dans l’ordre trigonométrique ξ0 = 1, ξ1, ξ2,..., ξn on trouve que, ξj.ξk = ξj+k si j + k < n, et ξn-j-k sinon.
La méthode de Vandermonde consiste à calculer des sommes partielles de racines, qui peuvent s’exprimer comme des images de fonctions rationnelles en des polynômes symétriques. Ceci permettrait de calculer ses sommes partielles, puis d’appliquer une nouvelle décomposition de chaque somme en sous-sommes et de calculer ces sous-sommes. En réitérant, il a l’espoir d’obtenir des sous-sommes composées chacune d’une unique racine et de conclure. Cette méthode lui permet de résoudre le cas où n est égal à 11, mais une méthode générique reste hors de portée. Il a toutefois résolu une équation du 11e degré qui n’avait aucune factorisation évidente autre que celle associé au terme (X - 1)[23].
Pour résoudre l’équation cyclotomique de degré quelconque, il reste encore un problème combinatoire. Comment associer les racines pour en faire des sommes partielles, solutions d’équations de degrés moindres ? Problème que ne résout pas Vandermonde. L’article détaillé propose une résolution pour les degrés 5 et 17.
Synthèse de Lagrange
Article détaillé : Polynôme symétrique.Dans son mémoire de 1771[H 6], Lagrange réalise une synthèse de toutes les méthodes utilisées dans le passé pour résoudre l’équation algébrique de petit degré. À l’aide de cette synthèse, il développe une méthode, qui s’applique aux degrés 2, 3 et 4. Il montre de plus que cette méthode ne peut aboutir dans le cas général si le degré est plus élevé. Sa démarche, même si elle aboutit à un échec, est à beaucoup d’égards un véritable pas en avant.
Tout d’abord, la méthode est suffisamment générale pour que toutes les tentatives précédentes ne soient que des cas particuliers de la sienne. Il met ainsi un terme à l’époque des méthodes empiriques de Tschirnchaus ou Euler, nécessairement vouées à l’échec.
Il reprend l’idée de Vandermonde d’utiliser les fonctions symétriques ainsi que les relations entre les coefficients et les racines et montre l’importance des n! permutations des racines pour la résolution du cas général. Il établit à ce propos deux théorèmes préfigurant la théorie des groupes. Le premier est que les n! permutations d’un n-uplets ont comme image par une fonction de n variables un ensemble de cardinal un diviseur de n!. Ce résultat est un ancêtre de ce que l’on appelle maintenant le théorème de Lagrange sur les groupes. Le deuxième concerne les fonctions qu’il qualifie de semblables et qui sont invariantes par le même sous-groupe de permutation. Ce résultat anticipe les théorèmes sur les suites de sous-groupes que l’on trouve dans la théorie de Galois ou dans le Théorème de Jordan-Hölder. La conclusion de Lagrange est pessimiste : « d’où il s’ensuit que, si la résolution algébrique des équations de degrés supérieurs au quatrième n’est pas impossible, elle doit dépendre[24] [...] » L’idée d’une impossibilité de résolution algébrique de l’équation est émise. Le chemin est tracé, soit pour trouver une méthode générale de résolution, soit pour montrer l’inexistence d’une telle méthode. La solution réside dans une analyse combinatoire des possibles permutations des racines. La conclusion est analogue à celle de Vandermonde pour le polynôme cyclotomique, mais cette fois, elle valable dans le cas général.
En parallèle des travaux de Vandermonde et de Lagrange, les développements de l’analyse ont fait perdre beaucoup d’intérêt au problème millénaire de la résolution d’une équation. À l’époque des mathématiques arabes, cette résolution était une méthode de calcul numérique essentielle. Al-Buruni souhaitait résoudre l’équation cubique pour calculer des sinus de tiers d’angle déjà connue[ADD 22]. Dès l’aube du XIXe siècle, l’analyse offre des méthodes beaucoup plus efficaces pour calculer des racines. Les résultats de Lagrange montrent qu’il faudra de plus, soit beaucoup de calculs, soit une grande idée, pour mettre un point final à cette question. De plus, elle risque fort de prendre la forme d’un constat d'échec, peu prometteur en termes de progrès des mathématiques. Cet environnement n’est pas favorable pour motiver des mathématiciens déjà renommés par ailleurs.
Progrès de Gauss
Article détaillé : Arithmétique des polynômes. Carl Friedrich Gauss pousse plus loin les travaux initiés par Vanermonde sur les polynômes cyclotomiques. Il use pour cela d’une approche structurelle, qui préfigure l’avenir de l’algèbre.
Carl Friedrich Gauss pousse plus loin les travaux initiés par Vanermonde sur les polynômes cyclotomiques. Il use pour cela d’une approche structurelle, qui préfigure l’avenir de l’algèbre.
Gauss ouvre le siècle suivant en apportant des éléments de réponses, sur les questions de Vandermonde et de Lagrange. Avancer dans la théorie des équations suppose le choix de bonnes fonctions rationnelles, invariantes par certaines permutations des racines. Lagrange l’a clairement montré et Vandermonde a émis l’hypothèse qu’elles devaient exister pour l’équation cyclotomique. Le nombre de permutations augmente rapidement en fonction du degré n du polynôme, il en existe factorielle n, soit déjà 120 pour le degré 5. L’approche aléatoire imposerait une quantité de calcul rapidement rédhibitoire. Gauss tient compte de cet acquis et change radicalement les méthodes d’analyse.
Il ne s’attaque pas au problème général, mais uniquement à l’équation cyclotomique, qu’il appelle « la théorie de la division du cercle »[H 7]. Sa méthode préfigure la démarche-clé du XIXe siècle, toujours en vigueur. Au lieu d’étudier directement le polynôme, il analyse la structure de l’ensemble des polynômes muni de son addition et de sa multiplication. Cette structure possède des points communs avec celle des entiers, il en conclut que cette branche des mathématiques « n’appartient pas par elle-même à l’arithmétique, mais ses principes ne peuvent être puisés que dans l’arithmétique transcendante. Ce résultat pourra sembler aux géomètres aussi inattendu que les vérités nouvelles qui en dérivent »[H 7]. Par arithmétique transcendante, Gauss entend ce que l’on appelle maintenant la théorie algébrique des nombres. En termes contemporains, l’analogie provient du fait que si les coefficients sont choisis dans un corps commutatif, l’anneau des polynômes et celui des entiers sont tous les deux euclidiens. Il va considérer les ensembles de polynômes en choisissant les coefficients les plus divers. Le cas où ils sont entiers l’amène à démontrer un lemme qui porte son nom, montrant le caractère factoriel de cette structure. Il utilise une de ses découvertes, l’arithmétique modulaire et travaille aussi sur des polynômes à coefficients sur les corps finis. Cette démarche impose l’usage du polynôme formel au détriment de la fonction polynôme, remettant ainsi à l’honneur la conception de Viète du polynôme.
Pour choisir les bonnes permutations, Gauss remarque qu’elles sont liées à la structure du groupe multiplicatif des racines, ou plus exactement celui de ses automorphismes. Dans le cas du polynôme cyclotomique, les racines sont les racines nièmes de l’unité et elles forment un groupe commutatif. À la différence de Lagrange, il perçoit l’importance de la loi du groupe, qui permet de combiner les différents éléments, alors que Lagrange se limitait à un simple dénombrement. Cette opération se traduit par des sommes de Gauss, qui permettent de trouver les sommes partielles imaginées par Vandermonde. Il en profite pour résoudre une conjecture qu’avaient vainement tenté de démontrer Euler et Legendre[25] : la loi de réciprocité quadratique.
Si Gauss fait progresser la théorie des équations, son objectif est néanmoins différent ; il met à jour une connexion inattendue entre la théorie des nombres et celle des équations.
Solution d'Abel
Article détaillé : Théorème d'Abel (algèbre). Niels Henrik Abel montre l’impossibilité de la résolution par radicaux de l’équation algébrique, dans le cas général, mettant fin à la quête millénaire et centrale de la théorie des équations. Son résultat est passé sous silence.
Niels Henrik Abel montre l’impossibilité de la résolution par radicaux de l’équation algébrique, dans le cas général, mettant fin à la quête millénaire et centrale de la théorie des équations. Son résultat est passé sous silence.
L’éventuelle impossibilité de la résolution par radicaux du cas général fait son chemin. Paolo Ruffini publie quatre mémoires à ce sujet, en 1799, 1804[H 8] puis en 1808 et 1813[26]. Pour la première fois, est déclarée clairement cette impossibilité. Sa tentative pour le montrer suit la démarche de Lagrange et consiste à montrer que l’usage d’une équation auxiliaire ne permet pas, pour le degré 5, d’abaisser systématiquement le degré de l’équation initiale. Il établit que, si une fonction symétrique de cinq variables prend strictement moins de cinq valeurs par permutations des variables[27], alors elle n’en prend pas plus de 2. En conséquence, si la méthode de Tschirnhaus fonctionnait, elle réduirait une équation du cinquième degré à une équation du deuxième degré, ce qui n’est pas possible dans le cas général. Cette approche est lacunaire[28]. Rien n’indique qu’une approche radicalement différente de celles décrites par Lagrange ne pourrait aboutir[H 9].
Pour conclure de manière définitive, il fallait raisonner différemment que ne l’avaient fait Lagrange ou Ruffini. Niels Abel l’exprime ainsi : « [...] on se proposait de résoudre les équations sans savoir si cela était possible. Dans ce cas, on pouvait bien parvenir à la résolution, quoique ce ne fût nullement certain [...] Au lieu de demander une relation dont on ne sait pas si elle existe ou non, il faut se demander si une telle relation est en effet possible[ADD 23]. » En 1826, Abel part du résultat et suppose qu’il existe une formule, fonction rationnelle de radicaux, qui donne la solution d’une équation de degré 5. Il sait qu’elle est à même d’exprimer 5 racines différentes et qu’en conséquence, elle possède un comportement précis vis-à-vis des permutations des variables, déjà étudiées par Vandermonde, Lagrange puis Cauchy[ADD 24]. Il démontre que ce comportement introduit une absurdité[H 10].
Ce résultat reste à ce moment fort peu connu. Son article, pourtant envoyé à Gauss, Legendre et Cauchy n’intéresse personne. Gauss, qu’Abel souhait rencontrer dans sa ville de Göttingen, ne le reçoit pas[29]. D’un point de vue théorique, le résultat d’Abel apparaît tout d’abord comme la mort de la théorie des équations, du moins sous sa forme classique, et l’intérêt de s’investir dans une branche condamnée semble limité. Et puis, à quoi bon souhaiter exprimer les racines sous forme de radicaux ? En termes algébriques, comme le fait remarquer Gauss, il est plus simple de noter les racines x1,..., xn et l’expression sous forme de radicaux est un peu désuète. En termes de calcul numérique, cette méthode est lourde, comparée à ce que permet l’analyse. Il suffit, pour s’en rendre compte, de regarder l’expression de la partie réelle d’une des racines de l’équation X 17 - 1 = 0, trouvée par Gauss :

Abel ne trouve une première notoriété que posthume, avec son travail sur les intégrales elliptiques, et non avec son travail sur la théorie des équations[30].
Les théories de Galois
Œuvre de Galois
Article détaillé : Théorie de Galois.Évariste Galois naît en 1811, soit huit ans après Abel. Il n’a que 14 ans lors de la publication du théorème de son prédécesseur. Quand il trouve une nouvelle démonstration, il n’est probablement pas au courant de l’article d’Abel[31]. De façon certaine, sa démarche est différente. Elle entre plus dans la tradition de Gauss que dans celle de Lagrange ou de Cauchy. Il s’intéresse aux permutations qui laissent invariants tous polynômes en plusieurs indéterminées, appliquées aux racines, tout comme Lagrange, Cauchy ou Abel. Cependant, à l’image de Gauss, il concentre ses efforts sur l’étude de la loi de composition, il précise : « dans le groupe de permutations dont il s’agit ici, la disposition des lettres n’est point à considérer, mais seulement les substitutions de lettres par lesquelles on passe d’une permutation à l’autre »[H 11]. Il donne le nom de groupe formel à cette structure, qu’il considère comme incarnée par des permutations, mais qui possède aussi une existence abstraite. À la différence de Gauss, il n’étudie pas le cas particulier de l’équation cyclotomique, dont le groupe est très simple, car cyclique, mais le cas général.
À l’aide de cet outil maintenant appelé groupe de Galois, le mathématicien établit trois résultats, le théorème de l'élément primitif, le théorème fondamental de la théorie de Galois et une nouvelle mouture du théorème d’Abel, plus profonde que la précédente puisqu’il donne une condition nécessaire et suffisante de résolubilité. G. Verriest décrit les travaux du mathématicien dans les termes suivants : « [...] le trait de génie de Galois c’est d’avoir découvert que le nœud du problème réside non pas dans la recherche directe des grandeurs à adjoindre, mais dans l’étude de la nature du groupe de l’équation. Ce groupe [...] exprime le degré d’indiscernabilité des racines [...]. Ce n’est donc plus le degré d’une équation qui mesure la difficulté de la résoudre mais c’est la nature de son groupe[32]. » Un peu à l’image des réflexions de Lagrange, ces trois théorèmes font le tour complet de la théorie des équations. Mais en plus d’englober les méthodes passées, Galois donne aussi une vision qui permet de comprendre la nature de toute équation algébrique, résoluble ou non.
L’accueil qu’il reçoit est encore plus glacial que celui d’Abel. Cette fois-ci, Cauchy n’oublie pas l’article que lui envoie Galois, mais le perd carrément. Un nouvel envoi de ses travaux sur les équations elliptiques provoque le commentaire suivant : « le raisonnement n’en est pas assez clair, ni assez développé pour lui permettre d’en juger la rigueur[33]. »
Naissance de l'algèbre moderne
 Pour Camille Jordan, le premier à utiliser l’expression théorie de Galois, les travaux de cet inventeur portent sur l’analyse des groupes et des applications linéaires, pris sous l’angle structurel.
Pour Camille Jordan, le premier à utiliser l’expression théorie de Galois, les travaux de cet inventeur portent sur l’analyse des groupes et des applications linéaires, pris sous l’angle structurel.
On utilise souvent les expressions d'« inventeur » ou de « père » de l’algèbre moderne pour désigner Galois[34]. Alain Connes, un spécialiste du domaine, précise : « Galois, à l’âge de 19 ans, a déjà à son actif des résultats mathématiques d’une portée incomparable qui sont l’acte de naissance des mathématiques contemporaines »[35]. Pour comprendre la raison d’être d’un tel propos, il est utile de regarder ce qu’est l’algèbre du milieu de XIXe siècle. En 1854, Serret publie un livre Cours d’Algèbre supérieur qu’il définit comme « l’Algèbre est, à proprement parler, l’analyse des équations, les diverses théories partielles qu’elle comprend se rattachent toutes, plus ou moins, à cet objet principal[H 12]. » Cette vision, que confirmait déjà Al-Khayyam dans son grand traité écrit au XIe siècle[ADD 25], était dès l’époque de Gauss puis de Galois, déjà devenue obsolète.
Depuis Al-Khawarizmi et jusqu’à la fin du XVIIIe siècle, la théorie des équations est une théorie de formules. Les maîtres arabes, tout autant que ceux de la Renaissance italienne, procèdent de cette logique pour résoudre les équations de bas degrés, ou quand à l’aide d’un discriminant, ils établissent l’existence de racines multiples. Le langage de Viète, ne sert finalement qu’à mieux les exprimer, ce qui permet de trouver d’autres formules comme les relations entre coefficients et racines. Lagrange entre dans cette tradition dans ses réflexions, même si finalement il en établit le caractère aléatoire et aventureux pour les degrés plus élevés.
La logique de Galois est en rupture par rapport à cet héritage millénaire. Liouville, qui la redécouvre 11 ans après la mort de son auteur, la présente à l’Académie des sciences avec les propos suivants : « Cette méthode, vraiment digne de l’attention des géomètres, suffirait seule pour assurer à notre compatriote un rang dans le petit nombre des savants qui ont mérité le titre d’inventeur[H 13]. » Ce sont, avant tout, des structures que Galois met en évidence. La première, déjà citée, est celle de groupe. La redécouverte des idées de Galois la met en première ligne : Cauchy ne publie pas moins de vingt-cinq articles sur cette question après la présentation de Liouville, dont un porte encore son nom[H 14]. En 1870, Camille Jordan publie un livre présentant les travaux de Galois essentiellement comme une théorie sur les groupes[H 15]. Un autre aspect n’est pas passé sous silence. Chez Galois, les éléments du groupe sont aussi des symétries[Note 14] d’un espace géométrique. Cet angle d’analyse, que l’on considère maintenant comme de l’algèbre linéaire est l’une des idées fondatrices développées dans le livre de Jordan. Ces aspects structurels, à travers l’analyse des diviseurs de la dimension d’un espace vectoriel, est la manière la plus simple de démontrer des conjectures plusieurs fois millénaires, à savoir la trisection de l’angle ou la duplication du cube. Le titre du livre de Jordan Traité des substitutions et des équations algébriques est à cet égard évocateur : le terme de substitution est, en effet, celui utilisé à l’époque pour désigner une application linéaire. Plus tard, à la fin du XIXe siècle, à la suite des travaux de Dedekind et Kronecker, Weber identifie la théorie de Galois à celle des corps commutatifs[H 16].
La logique structurelle initiée par Galois est à l'origine d'une profonde mutation, elle ne touche pas uniquement le périmètre de la théorie des équations qui devient l'algèbre au sens contemporain du terme, mais toute la mathématique[36].
Annexes
Bibliographie
- A. Dahan-Dalmedico et J. Peiffer, Une Histoire des mathématiques - Routes et dédales [détail des éditions]
Le plan et le contenu général de l'article sont issus en majeure partie de cette référence. Chaque paragraphe est enrichi par des références plus spécialisées.- R. Rashed, Entre arithmétique et algèbre : recherches sur l'histoire des mathématiques arabes, Les Belles lettres, Paris, 1984.
Les paragraphes Algèbre arabe et La géométrie au service de l'algèbre sont essentiellement issus de cette référence.- P. Freguglia, « Sur la théorie des équations algébriques entre le XVIe et XVIIe siècles », Bollettino di storia delle scienze matematiche, vol. 14, no 2, 1994, p. 259-298.
Cette référence complète le livre Une Histoire des mathématiques - Routes et dédales pour les paragraphes Appropriation européenne et Viète, Fermat et Descartes.- Nicolas Bourbaki, Éléments d'histoire des mathématiques [détail des éditions]
Seuls trois chapitres ont été consultés. Ils sont utilisés pour la rédaction des paragraphes : L'évolution de l'algèbre, Calcul infinitésimal et Polynômes et corps commutatifs. Leur lecture a influencé les paragraphes Viète, Fermat et Descartes et Calcul infinitésimal.- D. Flament, Histoire des nombres complexes - Entre algèbre et géométrie, CNRS éditions, 2003 (ISBN 2271061288).
Cette référence couvre une période allant du XIIIe au XIXe siècles. Elle n'a été consultée que pour la période couverte par le paragraphe « Imaginaires et nombres complexes ».- B. Fine, G. Rosenberg, The fundamental theorem of algebra, Springer, 1997 (ISBN 0387946578).
Cette référence est celle qui couvre le paragraphe Théorème fondamental de l'algèbre.- Jean Dieudonné (dir.), Abrégé d'histoire des mathématiques 1700-1900 [détail des éditions]
Seuls les chapitres L'analyse mathématique au XVIIIe siècle, L'algèbre et la géométrie jusqu'en 1840 et L'algèbre depuis 1840 ont été consultés. Cette référence est la source complémentaire sur la dernière partie de l'histoire, commençant à partir du paragraphe Vandermonde et le polynôme cyclotomique.Liens externes
- H. Bellosta, « À propos de l’histoire des sciences arabes », SMF Gazette, no 82, 1999.
- S. Maronne, Trois jalons dans l’histoire de la théorie des équations algébriques d’al-Khawarizmi à Descartes, IURM d’Auvergne.
- [PDF] A. Gloden, Paragraphe : « Théorie des équations, » du texte intitulé : Viète père de l’algèbre moderne de l’Université de Bruxelles.
- (en) J. J. O'Connor, E. F. Robertson, The fundamental theorem of algebra par le site historique de l’Université de St Andrew.
- O. Gebuhrer, Invitation à des réflexions sur la résolution algébrique des équations, IREM de Strasbourg.
- C. Ehrhardt, Le mémoire d’Évariste Galois sur les conditions de résolubilité des équations par radicaux, Bibnum : textes fondateurs de la science analysés par les scientifiques d´aujourd´hui.
- A. Connes, La pensée d’Évariste Galois et le formalisme moderne.
Notes
- « Équations, théorie des », Encyclopédie Encarta.
- Le terme équivalent s’applique lorsque quelques transformations permettent de reformuler l’équation sous la forme de la recherche des racines d’un polynôme.
- Voir par exemple le papyrus Rhind.
- Voir le paragraphe Diffusion en Europe.
- On trouve néanmoins des exceptions. Un contre exemple est le titre du tome III : Théorie des équations d’un livre consacré à l’analyse : J. Favart, Cours d’analyse de l’école polytechnique, Gauthier-Villars, 1963.
- Voir à ce sujet l’article : Construction de l'anneau des polynômes.
- Voir à cet égard le Livre II des Éléments d'Euclide.
- Voir à ce sujet l’article : Algèbre géométrique.
- La valeur b/2 est plus petite que √(b/2)2 + (b/3)3), ce nombre est donc négatif. Considérer ensuite la longueur de l’arête d’un cube ayant ce nombre négatif pour volume, procède d’une logique incompréhensible à cette époque.
- Chez Michael Stifel, Jacques Pelletier et Jean Borrel, cf. A. Dahan-Dalmedico et J. Peiffer, Une Histoire des mathématiques - Routes et dédales [détail des éditions], p. 109.
- Ce paradoxe est une des raisons qui pousse à l’usage du symbole i au lieu de l’ambigu √-1.
- Voir Formule de Moivre.
- Si l’équation est dite cyclotomique, le polynôme ne l’est pas. Une définition précise est donnée dans l’article Polynôme cyclotomique.
- Le terme de symétrie est à prendre ici au sens d’automorphisme d’un espace vectoriel de dimension finie.
Références
A. Dahan-Dalmedico et J. Peiffer, Une Histoire des mathématiques - Routes et dédales [détail des éditions]
- p. 83.
- p. 75.
- p. 76.
- p. 85.
- p. 85, un exemple d’équation de cette nature est donné dans l’article inconnue (mathématiques).
- p. 103.
- p. 95.
- p. 97.
- p. 105.
- Celle citée est extraite p. 106.
- p. 108.
- p. 109.
- p. 110.
- p. 111.
- chap. 5 intitulé « La limite : de l’impensé au concept », p. 168.
- p. 192.
- p. 249.
- p. 253.
- p. 254.
- p. 252.
- Ce paragraphe correspond aux idées de la page 113.
- p. 94.
- Cette citation d’Abel est reprise p. 118.
- Cauchy avait généralisé le résultat de Ruffini au cas de n variables en 1815, p. 118.
- p. 94.
Autres références :
- C’est par exemple le choix de : « Sur l’histoire du théorème fondamental de l’algèbre : théorie des équations et calcul intégral », Archive for History of Exact Sciences, vol. 42, no 2, p. 91-136.
- On trouve par exemple l’expression Théorie analytique des équations différentielles ordinaires, par le programme des cours LMD de l’université Pierre et Marie Curie à Paris.
- Cette question est extraite d’une tablette conservée au British museum sous le numéro BM 13901 : L’algèbre babylonienne, par l’IREM de Rennes. La notation 6 15 est ambiguë, nous avons choisi ici une des significations possibles.
- Collectif IREM-APMEP de Poitiers, (Institut de recherche sur l'enseignement en mathématiques - Association des professeurs de mathématiques de l’enseignement public), Histoire de symboles, chapitre 12 : La première inconnue, 2003, [lire en ligne]
- P. Ver Eecke, Diophante d’Alexandrie – Les Six Livres Arithmétiques et le Livre des Nombres Polygones, Desclée de Brouwer, Liège, 1926, p. 2.
- R. Rashed, Entre arithmétique et algèbre : recherches sur l’histoire des mathématiques arabes, Les Belles lettres, Paris, 1984.
- J. Dhombres G. Beaujouan G. Mazars J.-C. Martzloff R. Rashed, Le matin des mathématiciens, Belin, 1985 (ISBN 9782701105338), p. 146.
- L. Rodet, l’algèbre d’Al-Khârizmi et les méthodes indienne et grecque, lire sur Gallica, p. 24.
- Christian Drouin, « Muhammad Al-Khâwârîzmî » sur Équipe de mathématiques de l'académie de Bordeaux, 4 avril 2001. Consulté le 25 avril 2009
- H. Bellosta indique : « Son successeur Sharaf al-Dîn al-Tûsî (XIIe siècle) va étudier de façon plus rigoureuse les conditions d’existence de ces points d’intersection, dont l’abscisse détermine la racine positive demandée ; ceci va l’amener à se pencher sur des problèmes de localisation et de séparation des racines et l’obliger à définir la notion de maximum d’une expression algébrique (en introduisant la dérivée formelle d’un polynôme). Une autre innovation d’al-Tûsî consiste à traiter, en même temps que la résolution géométrique, la résolution numérique des équations du troisième degré. Il développe pour cela une variante de la méthode de Ruffini Horner. » : [PDF] « À propos de l’histoire des sciences arabes », SMF Gazette, no 82, 1999.
- On peut lire à ce sujet le site de M. Bichaoui, L’Histoire des équations du 3e degré.
- B. Hauchecorne, D. Surateau, Des mathématiciens de A à Z, Ellipses, Paris, 1996 (ISBN 2729846832).
- « Lodovico Ferrari », Encyclopædia Britannica
- P. Freguglia, « Sur la théorie des équations algébriques entre le XVIe et XVIIe siècles », Bollettino di storia delle scienze matematiche, vol. 14, no 2, 1994, p. 259-298.
- (en) F. Cajori, A History of Mathematics, The Macmillan Co, New York, 1919, p. 139.
- Nicolas Bourbaki, Éléments d’histoire des mathématiques, Springer, 2007 (ISBN 3540339817), p. 71.
- M. Blay, « Deux moments de la critique du calcul infinitésimal : Michel Rolle et George Berkeley – Études sur l’histoire du calcul infinitésimal », revue Histoire des sciences, vol. 39, no 3, 1986, p. 223-253.
- (en) T. A. Broadbent, « The History of Ancient Indian Mathematics by C. N. Srinivasiengar », The Mathematical Gazette, vol. 52, no 381, 1969, p. 307.
- Franck Duffaud, « Mathématiciens italiens du XVIe siècle » sur Math93 : Une histoire des mathématiques, 1999. Consulté le 25 avril 2009
- (en) B. Fine, G. Rosenberg, The fundamental theorem of algebra, Springer, 1997, (ISBN 0387946578).
- C. Gilain, « Sur l’histoire du théorème fondamental de l’algèbre : théorie des équations et calcul intégral », Archive for History of Exact Sciences, vol. 42, no 2, p. 91-136.
- Jean-Yves Briend, Le théorème fondamental de l'algèbre (version moderne de cette preuve, la no 5), Centre de mathématiques et informatique de l'université de Provence Aix-Marseille, 30 janvier 2006, [PDF] [lire en ligne]
- Cette lecture du traité de Vandermonde provient de : J. Dieudonné, Abrégé d’histoire des mathématiques, 1700-1900, Hermann, 1996 (ISBN 2705660240).
- Extrait du texte précédemment cité. Il provient de l’analyse suivante : O. Gebuhrer, [PDF] Invitation à des réflexions sur la résolution algébrique des équations, IREM de Strasbourg
- Cyril bandelier, « Legendre, Gauss, Jacobi et les autres... » sur Laboratoire d'informatique de Paris-Nord (université Paris 13), 23 juillet 1998. Consulté le 25 avril 2009
- J. J. O'Connor E. F. Robertson, Paolo Ruffini, par le site de l'université de St Andrew.
- Nicolas Bourbaki, Éléments d'histoire des mathématiques, Springer-Verlag, (réédition 2006) (ISBN 3540339388), p. 104.
- Nicolas Bourbaki, Éléments d'histoire des mathématiques, Springer-Verlag, (réédition 2006) (ISBN 3540339388), p. 103.
- J. J. O'Connor E. F. Robertson, Niels Henrik Abel, université de St Andrew.
- Sur les travaux d’Abel, on peut consulter le site, extrait du livre : B. Hauchecorne, D. Surateau, [PDF] Des mathématiciens de A à Z, Ellipses, Paris, 1996 (ISBN 2729846832).
- C'est ce qu'affirme la source : (en) P. Pesic, Abel's Proof: An Essay on the Sources and Meaning of Mathematical Unsolvability, MIT Press, 2004 (ISBN 0262661829), p. 105.
- G. Verriest, Œuvres Mathématiques d’Évariste Galois, Gauthier-Villars, Paris, 1951.
- Franck Duffaud, « Évariste Galois » sur Math93 : Une histoire des mathématiques, 1999. Consulté le 25 avril 2009
- On trouve une expression de cette nature dans le très officiel site : Ambassade de France, « Lancement du programme de bourses « Evariste Galois » », Ambassade de France au Vietnam.
- A. Connes, La pensée d’Évariste Galois et le formalisme moderne
- André Lichnerowicz utilise les termes suivants, pour décrire la mutation dont Galois peut être pris comme un symbole : « Au lieu de subir les structures et de les reconnaître un peu au hasard, la mathématique s'efforcera de les dominer » : L'activité mathématique et son rôle dans notre conception du monde, Séance du 27 février 1965 au Collège de France.
Sources historiques
- I. Newton, De analysi per aequationes numero terminorum infinitas, W. Jones, Londres, 1711 (première publication en 1669).
- Cette démonstration est l’œuvre de P. O. Bonnet : P Appell, « Notice sur la vie et les travaux de Pierre Ossian Bonnet », Comptes rendus de l’Académie des Sciences, vol. 117, 1893, p. 1013-1024.
- René Descartes, La géométrie, 1637.
- L. Euler, Recherches sur les racines imaginaires des équations, Histoire de l’Académie Royale des Sciences et des Belles-Lettres de Berlin, 1751.
- A. T. Vandermonde, Mémoire sur la résolution des équations, Histoire de l’Académie royale des sciences, 1771.
- Joseph-Louis Lagrange, Réflexions sur la résolution algébrique des équations, Nouveaux mémoires de l’académie royale des sciences et belles lettres de Berlin, 1771, lire sur Gallica
- Carl Friedrich Gauss, Disquisitiones arithmeticae, 1801 (page XV dans l’édition de 1807), traduite en français par Poullet-Delisle et publié aux éditions Jacques Gabay en 1989 (ISBN 2876470543) lire sur Gallica
- P. Ruffini, La théorie générale des équations dans laquelle il est démontré qu’il est impossible de donner les solutions générales des équations de degré strictement supérieur à 4, 1799, et Sur la détermination des racines d’équations numériques de degré quelconque, 1804.
- Lagrange précise : « Si les équations de degré supérieur au quatrième n'est pas impossible, elle doit dépendre de quelque fonctions racine, différentes de la précédente. » J-L Lagrange, Réflexions sur la résolution algébrique des équations, Nouveaux mémoires de l’académie royale des sciences et belles lettres de Berlin, 1771, p. 357.
- N. Abel, Démonstration de l’impossibilité de la résolution algébrique des équations générales qui passent le 4ième degré, Journal des Mathématiques. de M. Crelle, tome I, p. 65.
- Extrait de Evariste Galois, Sur les conditions de résolubilité des équations algébriques, Journal de Liouville, 1846.
- J. A. Serret, Cours d’Algèbre supérieur, deuxième édition, 1854, p. 1.
- J. Liouville, « Œuvres Mathématiques d’Évariste Galois Suivie d’un avertissement de Liouville », Journal des Mathématiques pures et appliquées, vol. XI, 1846.
- Augustin Louis Cauchy, Sur le nombre de valeurs égale ou inégales que peut acquérir une fonction de n variables indépendantes, quand on permute ces variables entre elles d’une manière quelconque, 1845.
- C. Jordan, Traité des substitutions et des équations algébriques, 1870.
- Heinrich Weber, Théorie de Galois, 1893.
Wikimedia Foundation. 2010.

