Theoreme de Rolle

Sommaire 1 Énoncé 2 Remarques 3 Applications 4 Histoire 5 Démonstration 6 Voir aussi

Énoncé

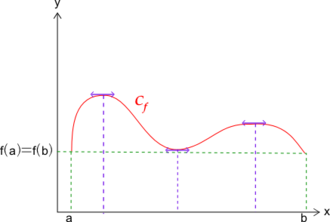
En analyse, le théorème de Rolle, en référence à Michel Rolle, s'énonce de la façon suivante :

Pour deux nombres réels a et b tels que et 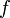une fonction à valeurs réelles continue sur et dérivable sur telle que :

alors il existe (au moins) un élément c de tel que :

.

Remarques

Le théorème de Rolle ne heurte pas l'intuition :

• Dire qu'il existe au moins un élément où la dérivée de f est nulle, c'est dire qu'il existe un point où la tangente à la courbe y=f(x) est horizontale.
• Dire que la fonction est dérivable sur l'intervalle, c'est dire que sa représentation graphique n'y a pas de points anguleux ni de discontinuités.

Les hypothèses nous garantissent par le Théorème des bornes que la fonction a un minimum et un maximum. Il y a donc bien un point c entre a et b tel que f(c) soit un maximum ou un minimum. En un tel point, la tangente à la courbe est horizontale.

Ce théorème permet d'intégrer les nécessaires propriétés topologiques des nombres réels dans l'analyse des fonctions réelles d'une variable réelle. Les propriétés topologiques sont intégrées à la démonstration à travers le Théorème des bornes.

Le théorème de Rolle ne s'étend pas aux fonctions d'une variable complexe ou à valeurs vectorielles. Par exemple, la fonction

est continue et dérivable sur l'intervalle fermé, et prend la même valeur aux deux bornes de l'intervalle ; mais sa dérivée ne s'annule en aucun point : pour tout .

Applications

Ce théorème est utilisé pour la démonstration du théorème des accroissements finis qui sert à l'analyse au développement limité d'une fonction et du théorème de Taylor. C'est la raison pour laquelle ce théorème est incontournable dans la construction de l'analyse.

Si P est un polynôme réel ayant au moins p racines réelles distinctes (p ≥ 2), alors son polynôme dérivé a au moins p - 1 racines réelles distinctes.

Histoire

Michel Rolle proposa une première démonstration de ce théorème à la fin du XVII^e siècle. Cependant, à cette époque, ce théorème était algébrique et ne concernait en rien l'analyse. En effet, il n'était formulé que dans le cadre des polynômes. Deux contemporains de Michel Rolle, Isaac Newton et Gottfried Wilhelm von Leibniz, fondent le calcul infinitésimal. Et personne n'est en mesure de comprendre que ce théorème deviendra plus tard l'un des piliers de l'analyse des fonctions d'une variable réelle à valeurs réelles. Plus grave encore, Michel Rolle jugea les travaux de calcul infinitésimal comme imprécis et défectueux. Il est vrai que selon nos critères actuels, ou même selon les critères que l'algèbre avait atteints à cette époque, en matière de logique et de formalisation, Michel Rolle avait raison. En revanche, les résultats de Newton et Leibniz étaient essentiellement justes et surtout fondateurs d'une nouvelle approche des plus fécondes dans l'histoire des mathématiques. Il ne s'en rendit compte qu'à la fin de sa vie, mais sans imaginer le destin que pourrait avoir le théorème qui porte désormais son nom.

Cette époque n'était pas mûre pour voir apparaître une formalisation rigoureuse de l'analyse. L'absence d'une compréhension profonde de la nature des nombres réels et, en conséquence, du concept de continuité ne permettait pas un progrès aussi rapide. Il fallut donc attendre un siècle et demi pour que l'énoncé de ce théorème soit subtilement modifié. En 1860 Pierre-Ossian Bonnet généralise le théorème aux fonctions dérivables. Cette généralisation change du tout au tout le statut de ce théorème. D'un résultat un peu anecdotique sur la théorie des polynômes réels, ce théorème devient une incontournable base de l'analyse réelle.

Démonstration

Si f est constante, la dérivée de f est nulle sur l'intervalle ouvert, donc la conclusion du théorème de Rolle est bien satisfaite. Dans le cas contraire, comme f est continue sur l'intervalle fermé borné [a, b], elle admet et atteint (d'après le théorème des bornes) un minimum global et un maximum global. Comme f n'est pas constante, le minimum global et le maximum global sont différents. Par conséquent le minimum global et le maximum global ne sont pas tout deux égaux à f(a) = f(b). Ainsi, l'un au moins de ces deux extrema est atteint en un point c appartenant à l'intervalle ouvert ]a, b[ .

On suppose ici, sans perte de généralité, que f(c) est maximum global. Les taux d'accroissement de la fonction f entre c et un deuxième point ont alors un signe connu :

• pour h strictement positif et tel que c+h appartienne à l'intervalle [a, b]

en considérant la limite quand h tend vers 0 par valeurs positives, on déduit que le nombre dérivé est négatif;

• pour h strictement négatif et tel que c+h appartienne à l'intervalle [a, b]

en considérant la limite quand h tend vers 0 par valeurs négatives, on déduit que le nombre dérivé est positif.

Au bout du compte, la dérivée de f au point c, étant à la fois positive et négative, est donc nulle.

La démonstration est analogue si f(c) est un minimum global, avec la seule différence que les signes des taux de variation sont les signes opposés à ceux de la démonstration qui précède.

C'est parce que c appartient à l'intervalle ouvert ]a,b[ que l'on a pu considérer ces taux d'accroissements : si c était égal à b le premier taux d'accroissement n'aurait pas de sens et si c était égal à a c'est le second taux d'accroissement qui ne serait pas défini.

Voir aussi

• Théorème des accroissements finis

• Portail des mathématiques