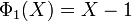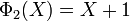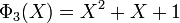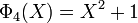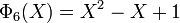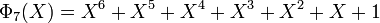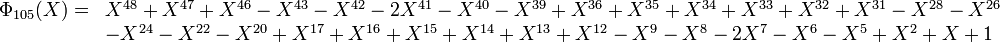Polynome cyclotomique

Polynome cyclotomique

Polynôme cyclotomique

Carl Friedrich Gauss

En mathématiques et plus particulièrement en algèbre, on appelle polynôme cyclotomique (du grec κυκλας:cercle et τομη:découpe) tout polynôme minimal d'une racine de l'unité et à coefficients dans un corps premier. Un corps premier est un corps engendré par l'unité de la multiplication. Les polynômes ainsi obtenus sont aussi ceux qui apparaissent dans la décomposition des polynômes Xn − 1 en produit de facteurs irréductibles.

Sur le corps des rationnels un polynôme cyclotomique possède des propriétés fortes, c'est un polynôme à coefficients entiers, de degré égal à φ(n) si la racine considérée est une racine primitive n-ième de l'unité, où φ désigne la fonction indicatrice d'Euler. Les racines du polynôme cyclotomique sont toutes les racines primitives n-ièmes de l'unité.

Dans le contexte des corps de caractéristique finie, il est nécessaire de faire appel à la théorie de Galois, ils apparaissent essentiels car tout polynôme irréductible est un polynôme cyclotomique (à l'exception du monôme unitaire de degré un).

D'une manière générale, le corps de décomposition encore appelé extension cyclotomique associé est une extension abélienne dont le groupe de Galois est cyclique.

L'analyse de ces polynômes permet la résolution de nombreux problèmes. Historiquement, la construction des polygones réguliers à la règle et au compas est celui qui a amené le développement du concept. Ils sont largement utilisés dans la théorie de Galois, pour la résolution d'équations algébriques et la compréhension de la structure des extensions abéliennes. Ils sont aussi au cœur de la cryptographie pour la conception de codes correcteurs.

Sommaire

Histoire

Naissance de la notion

Le traité d'analyse des polynômes cyclotomiques

Carl Friedrich Gauss (1777 - 1855) utilise dans ses Disquisitiones arithmeticae, parues en 1801, les polynômes cyclotomiques. Il apporte une contribution majeure à un problème ouvert depuis l'Antiquité : celui de la construction à la règle et au compas de polygones réguliers. Ces travaux servent de référence durant tout le siècle. Dans ce texte, Gauss détermine avec exactitude la liste des polygones constructibles, et donne une méthode effective pour leur construction jusqu'au polygone à 256 cotés. Ce problème de construction reçoit une réponse définitive par Pierre-Laurent Wantzel (1814 - 1848) dans un article[1] désormais célèbre.

Cette approche est novatrice et, à bien des égards, préfigure l'algèbre moderne :

Un polynôme n'apparaît plus comme un objet à part entière mais comme un élément d'un ensemble structuré. Si la notion d'anneau des polynômes n'est pas encore formalisée, sa structure euclidienne est découverte et représente l'outil de base de l'analyse de Gauss.

La résolution effective de l'équation cyclotomique conduit Gauss à considérer une structure finie : celle des permutations des racines. On les appelle maintenant période de Gauss. Là encore leurs propriétés algébriques permettent de trouver la solution. Cette approche préfigure l'utilisation de la théorie des groupes en algèbre et la théorie de Galois.

De nouvelles structures sont par la suite définies. La division euclidienne introduit la notion de reste et leur ensemble possède des propriétés algébriques fortes. Une telle structure est maintenant considérée comme un cas particulier de corps fini si le diviseur est un nombre premier. Gauss met en évidence de tels ensembles et utilise avant l'heure le transport de structure par morphisme entre deux anneaux pour montrer le caractère irréductible des polynômes cyclotomiques. Dans le même livre, il utilise ces mêmes structures pour résoudre un autre problème pressenti par Fermat (1601 - 1685) et formalisé par Euler (1707 - 1783) celui de la loi de réciprocité quadratique.

Dès cette époque, de nombreuses applications sont proposées. L'utilisation de la géométrie ne se limite pas à la construction à la règle et au compas. Le polynôme cyclotomique d'indice quatre permet la construction d'un nouvel ensemble de nombres algébriques celui des entiers de Gauss. Une branche mathématique naît : la théorie algébrique des nombres, elle simplifie la résolution d'équations diophantiennes et permet d'en résoudre de nouvelles.

Polynôme cyclotomique et équation algébrique

Évariste Galois

La recherche de solutions à l'équation polynômiale est un problème qui remonte aux premiers développements sur les polynômes par les mathématiciens de langue arabe. Si l'on cite généralement Al-Khawarizmi (783 850) comme précurseur[2] avec la résolution de six équations canoniques puis Gerolamo Cardano (1501 - 1576) pour la résolution du cas de degré trois[3] et Ludovico Ferrari (1522 - 1565) pour le quatrième degré, le cas général est resté longtemps mystérieux.

Joseph-Louis Lagrange (1736 - 1813) comprend que la résolution de ce problème général est intimement liée aux propriétés des permutations des racines[4]. Le cas particulier des polynômes cyclotomiques l'illustre. Le groupe des bonnes permutations, aujourd'hui appelé groupe de Galois, est non seulement commutatif mais de plus cyclique. Cette propriété, utilisée à travers le concept des périodes de Gauss, permet une résolution effective pour ce cas particulier.

Une analyse plus profonde par Paolo Ruffini[5] (1765 - 1822), Niels Henrik Abel[6] (1802 - 1829) et surtout par Évariste Galois[7] (1811 - 1832) montre que l'aspect commutatif du groupe est en fait une condition suffisante. Pour être précis, la condition indique que le groupe doit être décomposable en une suite de groupes emboîtés commutatifs. La question naturelle qui se pose alors est de déterminer les extensions du corps des rationnels dont le groupe de Galois est commutatif. Ces extensions sont appelées extensions abéliennes. La structure de corps associée au polynôme cyclotomique, appelée extension cyclotomique, en est un exemple. Qu'elle soit unique signifie que toute équation algébrique résoluble par radicaux se ramène d'une manière ou d'une autre à un polynôme cyclotomique. La réponse est positive : toute extension abélienne du corps des rationnels est un sous-corps d'une extension cyclotomique. La démonstration de ce résultat a demandé presque un demi-siècle d'effort[8]. Les artisans principaux sont Leopold Kronecker (1823 - 1891) et Heinrich Weber (1842 - 1913).

Si l'analyse des extensions abéliennes finies se termine avec le XIXe siècle, elle laisse ouvert un large champ de questions, par exemple en arithmétique. Il apparaît alors nécessaire de généraliser la notion de corps cyclotomique sur les extensions infinies. Le sujet est ouvert[9] par David Hilbert (1862 - 1943). Cet axe de recherche est appelé la théorie des corps de classe. Cette théorie est l'une des plus fructueuses au XXe siècle. On peut citer par exemple le théorème de réciprocité[10] d'Emil Artin (1898 - 1962) qui résout le neuvième des problèmes de Hilbert, ou plus récemment, deux lauréats de la médaille Fields pour leurs travaux sur des généralisations de la théorie : Vladimir Drinfeld en 1990 ou Laurent Lafforgue en 2002.

Corps fini

Le développement de l'ébauche de la théorie des corps finis initié par Gauss demande plus de temps. À la fin du XIXe siècle, la théorie des groupes fait apparaître la nécessité de travailler sur d'autres extensions que celle des nombres rationnels. La représentations des groupes[11] impose à Frobenius (1849 - 1917) l'étude des corps de caractéristique finie. Ce sont les corps où la somme itérée de l'unité finit par être égale à zéro. Une analyse, à l'aide de la théorie de Galois montre que, dans ce contexte, la théorie des corps finis est essentielle. Sa connaissance suffit pour la compréhension de la structure des polynômes cyclotomiques dans le cas de la caractéristique finie.

L'analyse de ces corps est rapide, notamment grâce à l'apport de l'école américaine. Au début du XXe siècle, les travaux de Leonard Dickson (1874, 1954) puis de Joseph Wedderburn (1882, 1948) mettent en évidence leur structure. Dickson publie[12] la première étude systématique et Wedderburn démontre en 1905 son théorème stipulant que tout corps fini est commutatif. Les polynômes cyclotomiques sont essentiels car ils forment l'ensemble des polynômes irréductibles (à l'exception du monôme unitaire de degré un: X). Sur tous les corps de caractéristique finie, toutes les extensions finies sont cyclotomiques.

Durant la deuxième moitié du XXe siècle, un nouveau champ d'investigation utilise les corps finis : la cryptographie. Si la sécurité d'un code ne nécessite pas l'utilisation des polynômes cyclotomiques, en revanche la fiabilité, c’est-à-dire la capacité à corriger les erreurs utilise les polynômes, on parle alors de code correcteur. Ce type de code, pour être optimal, utilise les corps finis et les polynômes cyclotomiques. On peut citer par exemple le code de Hamming ou dans un cas plus général les codes permettant un contrôle de redondance cyclique. La dimension algorithmique est aussi largement étudiée.

Définition et exemples

Définition

On le note en général Φn(X). Le symbole X désigne une indéterminée, les polynômes dont il est question ici sont formels et non pas des fonctions. Cette question est importante si le corps premier n'est pas le corps 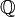\mathbb Q \, des nombres rationnels. En effet si le corps premier est fini, le nombre de fonctions polynômes est fini, alors que celui des polynômes formels ne l'est pas.

  • Un corps est dit premier s'il ne contient pas de sous-corps autre que lui-même.

C'est le plus petit sous-corps contenant 1 et tous ses itérés par l'addition. Si le corps est de caractéristique 0, il est égal à celui nombres rationnels, sinon il est isomorphe à Z/pZ, où p est la caractéristique du corps.

Dans le cas des rationnels, si la séquence finie (zk) décrit les racines nième primitives de l'unité dans le corps des complexes et φ la fonction indicatrice d'Euler, le polynôme Φn(X) est donné par:

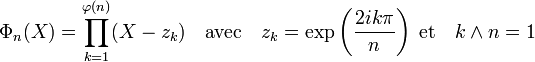
\Phi_n(X) = \prod_{k=1}^{\varphi(n)}(X-z_k)\quad\text{avec}\quad z_k=\exp\left(\frac{2ik\pi}{n}\right)\;\text{et} \quad k\land n = 1

Les polynômes cyclotomiques sont des polynômes unitaires à coefficients entiers. De plus, il est possible d'appliquer à Φn le morphisme d'anneau de Z[X] dans Z/pZ[X]. En particulier, si p est un nombre premier, Z/pZ est un corps fini. Une telle approche est utilisée pour démontrer le caractère irréductible du polynôme précédent.

On appelle corps cyclotomique ou extension cyclotomique le plus petit sous-corps du corps des nombres complexes contenant tous les nombres rationnels et une racine primitive n-ième de l'unité. Au lieu de se placer dans le corps des complexes, on aurait pu considérer les racines primitives n-ièmes de l'unité dans n'importe quelle extension (finie ou infinie) du corps des rationnels dans laquelle au moins une telle racine primitive existe. une telle extension contient une copie du corps cyclotomique.

Dans le cas où le corps n'est pas celui des rationnels, alors il est de cardinal fini p et p est un nombre premier. Il correspond à la structure Z/pZ et il est noté Fp. La théorie de Galois assure l'existence d'un plus petit sur-corps de Fp contenant une racine primitive n-ième de l'unité, on l'appelle aussi extension cyclotomique. Une fois encore, tout corps de caractéristique p (c’est-à-dire contenant Fp) et possédant une racine primitive n-ième de l'unité contient une copie de l'extension cyclotomique.

Remarque : Les propriétés associées à la définition sont démontrées à la suite dans cet article.

Premiers polynômes cyclotomiques

Les premiers polynômes cyclotomiques dans le cas des nombres rationnels sont :

\Phi_1(X) = X - 1\,
\Phi_2(X) = X + 1\,
\Phi_3(X) = X^2 + X + 1\,
\Phi_4(X) = X^2 + 1\,
\Phi_5(X) = X^4 + X^3 + X^2 + X + 1\,
\Phi_6(X) = X^2 - X + 1\,
\Phi_7(X) = X^6+X^5+X^4 + X^3 + X^2 + X + 1\,

Contrairement aux apparences, tous les coefficients des polynômes cyclotomiques ne sont pas 1, -1 ou 0 ; le premier polynôme cyclotomique pour lequel un coefficient entier distinct de 0, 1, -1 apparait est Φ105. 105 = 3×5×7 est le premier produit de trois nombres premiers impairs.

En effet :

\begin{array}{ll}\Phi_{105}(X) =& X^{48} + X^{47} + X^{46} - X^{43} - X^{42} - 2X^{41} - X^{40} - X^{39} + X^{36} + X^{35} + X^{34} + X^{33} + X^{32} + X^{31} - X^{28} - X^{26} \\ &- X^{24} - X^{22} - X^{20} + X^{17} + X^{16} + X^{15} + X^{14} + X^{13} + X^{12} - X^9 - X^8 - 2X^7 - X^6 - X^5 + X^2 + X + 1\end{array}

Dans le cas de la caractéristique finie, les polynômes précédents ne sont pas toujours irréductibles. On peut ainsi considérer le corps à deux éléments {0,1} noté F2. Il possède les tables d'opérations suivantes:

 +   0   1 
 0   0  1
 1   1  0
 .   0   1 
 0   0  0
 1   0  1

Le polynôme à coefficient dans Z Φ7(X) a pour image par le morphisme canonique dans F2[X] (qui aux coefficients pairs associe 0 et aux impairs 1) un polynôme qui possède bien les racines septièmes primitives de l'unité, mais ce polynôme n'est pas irréductible, en effet :

Dans \quad \mathbb F_2[X]: \quad X^6+X^5+X^4+X^3+X^2+X+1=(X^3+X^2+1)(X^3+X+1)\;

D'autres exemples sont donnés dans le paragraphe Polynôme irréductible de l'article sur les corps finis.

Propriétés remarquables

Cas du corps des nombres rationnels

Sans utiliser les outils sophistiqués que représente la théorie de Galois, il est possible de démontrer des propriétés fortes sur les polynômes cyclotomiques. Ce sont celles présentées dans ce paragraphe. Elles ont toutes été démontrées par Gauss dans son traité de 1801.

Pour un souci d'exposition, la définition initiale du polynôme cylotomique Φn(X) utilisée ici est, avec les notations de la définition :

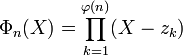
\Phi_n(X) = \prod_{k=1}^{\varphi(n)}(X-z_k)\;

Les propriétés suivantes sont vérifiées:

  • Le polynôme Xn − 1 se factorise comme suit, où le produit porte sur l'ensemble des entiers strictement positifs qui divisent n :
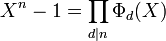
X^n-1= \prod_{d|n} \Phi_d(X)\;
Les six racines sixièmes de l'unité

L'identité sur les degrés fournit immédiatement :

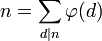
n=\sum_{d|n} \varphi(d)\;

Cette identité peut aussi s'obtenir par des considérations sur la fonction de Möbius ou par un raisonnement direct de dénombrement des éléments de l'anneau Z/n Z (lire indicatrice d'Euler).

  • Si p est un nombre premier, alors toutes les racines p-ièmes de l'unité sauf 1 sont des racines primitives p-ièmes primitives de l'unité, et l'égalité est vérifiée.
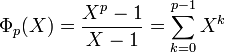
\Phi_p(X)=\frac{X^p-1}{X-1}=\sum_{k=0}^{p-1} X^k

Cette égalité fournit une expression du polynôme cyclotomique, à l'aide de la formule d'inversion de Möbius. La démonstration est proposée dans l'article Fonction de Möbius. Ici la fonction de Möbius est notée μ :

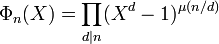
\Phi_n(X) = \prod_{d|n}(X^d - 1)^{\mu(n/d)}\;


  • Un polynôme cyclotomique ne possède que des coefficients entiers et son monôme dominant possède un coefficient égal à un.
  • Un polynôme cyclotomique est irréductible dans l'algèbre des polynômes à coefficients rationnels et dans l'algèbre des polynômes à coefficients entiers.

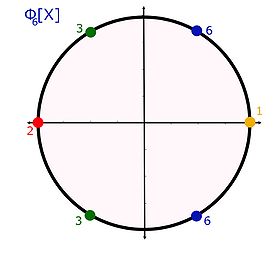
La figure de droite illustre ces propriétés. Le groupe des racines d'ordre six est décrit par quatre polynômes cyclotomiques, deux racines associées à des polynômes de degré un : un et deux, et quatre de degré deux avec les deux valeurs troisièmes et les deux valeurs sixièmes.


Démonstrations
  • Montrons l'égalité suivante:
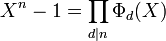
X^n-1= \prod_{d|n} \Phi_d(X)\;
Les deux polynômes de l'égalité à démontrer sont des polynômes de monômes dominants égaux à un (polynômes unitaires). De plus ils sont de degré n. Il suffit donc de démontrer par exemple que le premier divise le second.
Le polynôme Xn − 1 admet exactement n racines distincts, à savoir les n racines n-ièmes de l'unité. Étant de degré n, il n'admet donc aucune racine multiple. Il est donc simplement scindé, produit des monômes deux à deux premiers entre eux X-z où z parcourt les racines n-ièmes de l'unité. Or, toute racine n-ième est exactement une racine primitive d'ordre d pour un unique diviseur d de n. Par définition des polynômes cyclotomiques, z est une racine de Φd ; autrement dit, X-z divise Φd. De suite, Xn divise le produit des Φd pour d divisant n.
L'égalité se trouve établie.
  • Si p est un nombre premier, alors toutes les racines p-ièmes de l'unité sauf 1 sont des racines primitives p-ièmes de l'unité, et l'égalité suivante est vérifiée :
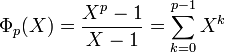
\Phi_p(X)=\frac{X^p-1}{X-1}=\sum_{k=0}^{p-1} X^k
Si z est une racine primitive p-ième de 1, alors l'ordre de z dans le groupe multiplicatif C* divise nécessairement p. Comme p est premier, l'ordre de z est 1 ou p. Le seul élément d'ordre 1 étant l'élément neutre 1, toute autre racine de p-ième est nécessairement une racine primitive d'ordre p.
Une autre preuve possible présuppose connu que l'indice d'Euler de p est p-1 : toutes les racines p-ièmes de l'unité sauf une doivent alors être primitives. Or 1 n'est une racine primitive d'un nombre premier. Ceci montre que le polynôme Xp - 1 n'admet que deux diviseurs X - 1 et le polynôme cyclotomique associé.
  • Un polynôme cyclotomique Φn(X) ne possède que des coefficients entiers et de coefficient dominant égal à un.
Le fait que le coefficient dominant soit égal à un est une évidence.
Montrons par récurrence sur n que le polynôme est à coefficients entiers.
Si n est égal à 1 alors le résultat est vrai car Φ1(X) = X - 1 (voir la section exemples).
Supposons la propriété vraie pour toute valeur inférieure ou égal à n. Alors la première proposition permet d'affirmer que:
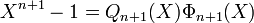
X^{n+1} -1 = Q_{n+1}(X) \Phi_{n+1} (X)\;

ou le polynôme Qn+1(X) est le produit de tous les polynômes cyclotomiques d-ièmes avec d divisant strictement n (ie d divise n et est distinct de n). Par hypothèse de récurrence, Qn+1(X) est le produit de polynômes unitaires à coefficients entiers et donc lui-même un polynôme unitaire à coefficient entier. Divisons alors le polynôme à coefficients dans les entiers Xn-1 par Qn+1(X) dans l'anneau Z[X] des polynômes à coefficients entiers. Cela est réalisable car Q est unitaire ; on obtient alors l'identité:

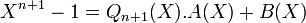
X^{n+1} -1 = Q_{n+1}(X).A(X)+B(X)\;

Avec A(X)et B(X) élément de Z[X], et B de degré strictement inférieur à n. Réalisons maintenant la division euclidienne dans l'anneau Q[X] l'anneau des polynômes à coefficients rationnels. Il existe une unique solution avec le degré de B(X) strictement inférieur à n+1. On en déduit que les divisions euclidiennes dans Q[X] et dans Z[X] donnent exactement le même résultat. En conséquence, B(X) est égal au polynôme nul et A(X) est égal au polynôme cyclotomique. Donc le polynôme cyclotomique est à coefficients entiers.

  • Un polynôme cyclotomique est irréductible.

Soit z le première des racines primitives n-ièmes. C’est-à-dire z = exp(2π.i/n). Soit M1(X) le polynôme minimal de z

M1(X) est un polynôme à coefficients entiers unitaire.

z est racine du polynôme Xn - 1 est donc son polynôme minimal divise ce polynôme. Il existe donc un polynôme à coefficients entiers tel que l'égalité suivante soit vérifiée:

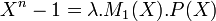
X^n-1=\lambda. M_1(X).P(X)\;

Où λ est choisi de telle manière à ce que le polynôme P(X) soit à coefficients entiers. La démonstration précédente a établi que dans ce contexte, λ.M1 (X) est aussi un polynôme à coefficients entiers. De plus comme Xn - 1 est unitaire, il en est de même pour M1 (X) et P(X) et λ est égal à 1.

Si p est un nombre premier qui ne divise pas n alors z p est racine de M1(X).

Raisonnons par l'absurde et supposons que cela ne soit pas le cas. Soit Mp (X) le polynôme minimal de z p alors Mp (X) ne divise pas M1 (X) mais divise Xn - 1. Il divise donc le polynôme P(X). Il existe donc un polynôme Q(X) vérifiant l'égalité suivante:

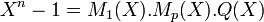
X^n-1=M_1(X).M_p(X).Q(X)\;

Un raisonnement analogue à celui sur P(X) montre que Q(X) est unitaire à coefficients entiers. z p est racine du polynôme Mp (X) et donc z est racine du polynôme Mp [Xp]. On en déduit que Mp [Xp] est un multiple de M1 (X). Il existe donc un polynôme unitaire R(X) à coefficients entiers vérifiant:

M_p[X^p]=M_1(X).R(X)\;

Par passage au modulo p, en remarquant que la formule du binôme devient

(\bar{A}+\bar{B})^p=\bar{A}^p+\bar{B}^p \mbox{ et donc } \bar{M}_p[X^p]=\bar{M}_p(X)^p en conséquence
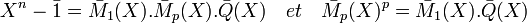
X^n-\bar{1}=\bar{M}_1(X).\bar{M}_p(X).\bar{Q}(X)\quad et \quad \bar{M}_p(X)^p=\bar{M}_1(X).\bar{Q}(X)

Soit D(X) un diviseur irréductible de degré strictement supérieur à 1 de M1 (X) dans l'anneau quotient (s'il n'en admet pas d'autres que 1 et lui-même sur les entiers, il n'en est pas de même sur l'anneau quotient) alors il divise aussi Mp (X) dans l'anneau quotient puisqu'il divise sa puissance. On en déduit que son carré divise Xn - 1 et D(X) divise la dérivée formelle de Xn - 1 dans l'anneau quotient (cf l'article polynôme formel). D(X) divise donc nXn-1 dans l'anneau quotient, et ce polynôme est non nul car n et p sont premiers entre eux. On en déduit que D(X) est égal à X car il est irréductible. Or X ne divise pas Xn - 1 dans l'anneau quotient. D'où une contradiction. En conséquence nous avons montré que Mp (X) est égal à M1 (X).

Si k est un nombre premier avec n alors z k est racine de M1(X).

Le nombre k est produit de q nombres premiers qui ne divisent pas n. Un récurrence sur q permet de conclure. Si k vaut 1 c'est évident. En supposant la propriété vraie pour le rang q-1, si z' est égal à z à la puissance le produit de q-1 nombres premiers ne divisant pas n, z' est racine de M1 (X) et le raisonnement précédent montre que z' à la puissance un nombre premier ne divisant pas n est encore racine de M1 (X), donc z à la puissance le produit de q nombres premiers ne divisant pas n est racine de M1 (X).

En conclusion, le polynôme minimal de z contient pour racine au moins toutes les racines du polynôme cyclotomique. Le polynôme cyclotomique divise donc le polynôme minimal. Comme ce dernier est irréductible, l'égalité est établie.

Cas de la caractéristique finie

Corps de décomposition

Article détaillé : Corps de décomposition.

Soit p la caractéristique du corps premier, ce corps est celui de l'arithmétique modulaire isomorphe à Z/p.Z. On peut considérer dans un tel corps un polynôme du type Xn - 1, par exemple dans F2[X] le polynôme X3 - 1. Dans le cas de Q, il existe une extension de corps celui des nombres complexes contenant les racines du polynôme. La théorie de Galois, à l'aide des exentions algébriques permet de trouver une extension dans lequel le polynôme est scindé, c’est-à-dire que l'extension contient toutes ses racines. Un tel corps est appelé corps de décomposition. Dans l'exemple cité, le corps est celui noté en général F4 contenant quatre éléments. Sa table est la suivante:

Illustration graphique du groupe multiplicatif de F4
 +   0   1   t   1+t 
 0   0  1  t  1+t
 1   1  0  1+t  t
 t   t  1+t  0  1
 1+t   1+t  t  1  0
 .   0   1   t   1+t 
 0   0  0  0  0
 1   0  1  t  1+t
 t   0  t  1+t  1
 1+t   0  1+t  1  t

Dans ce corps, t et 1 + t sont les deux racines supplémentaires du polynôme X3 - 1. L'étude des extensions algébriques montre que tout corps contenant les racines d'un polynôme contient un sous corps isomorphe à F4. En conséquence tout corps de caractéristique deux contenant les racines possède une copie exacte de F4. Les solutions trouvées et leur comportement algébrique sont donc toujours les mêmes. Ce résultat est général à toute extension finie et donc à tout polynôme cyclotomique.

La théorie des corps finis permet d'aller plus loin. Les seules extensions d'un corps premier Fp sont une extension de cardinal une puissance de p et il existe une et une unique extension de cardinal pm où m est un entier strictement positif. De plus, le groupe multiplicatif d'une telle extension est un groupe cyclique de cardinal pn - 1 (0 n'est pas élément du groupe multiplicatif car il n'a pas d'inverse). La figure de droite l'illustre dans le cas de F4, tout élément autre que 0 apparaît comme une racine de l'unité. La multiplication est représentée graphiquement comme on le fait pour le corps des complexes. En revanche, l'addition n'est pas représentée.

Automorphisme de Frobenius

Articles détaillés : Corps fini et Automorphisme de Frobenius.
Ferdinand Georg Frobenius

Dans le cas d'un corps fini de caractéristique p et de cardinal pd il existe un automorphisme digne d'intérêt: l'automorphisme de Frobenius. À un élément x du corps il associe xp. Cet automorphisme est un générateur du groupe de Galois et sa d-ième puissance est égale à l'identité. Pour cette raison et dans ce contexte on appelle souvent le groupe de Galois groupe de Frobenius. Cette égalité se traduit en terme polynomial par:

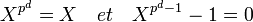
X^{p^d}=X\quad et \quad X^{p^d-1}-1=0\;

Et tout élément du corps différent de zéro est une racine de l'unité. Un polynôme irréductible autre de X (qui admet pour racine zéro) est un polynôme cyclotomique. La détermination des polynômes cyclotomiques correspond donc à un classement des polynômes irréductibles. On en déduit la proposition suivante:

  • Tout élément non nul d'un corps fini est une racine de l'unité et tout polynôme irréductible différent que X est un polynôme cyclotomique.

Soit z1 une racine primitive n-ième de l'unité. La théorie de Galois démontre que son polynôme minimal admet pour racines les images de z1 par le groupe de Frobenius, car un corps fini est une extension galoisienne du corps premier. Ce qui se traduit en termes mathématiques

  • L'ensemble des racines du polynôme cyclotomique de z1 est l'orbite de z1 par l'action du groupe de Frobenius notée Orb (z1). La formule du polynôme est la suivante:
\Phi_{z_1}[X]=\prod_{z \in Orb(z_1)} (X - z)\;

L'image par un automorphisme d'une racine n-ième primitive de l'unité est une racine primitive n-ième de l'unité, et:

  • Un polynôme cyclotomique d'indice n divise l'image du polynôme cyclotomique à coefficients entiers par le morphisme canonique de Z[X] dans Fp[X].

Il reste à savoir si les deux polynômes sont égaux, c’est-à-dire si l'orbite de z1 contient toutes les racines primitives n-ième de l'unité. L'exemple donné sur F2 montre que ce n'est pas toujours le cas. La théorie de Galois permet d'affirmer que le degré du polynôme cyclotomique de z1 est la dimension δ du corps de décomposition, considéré comme un espace vectoriel sur le corps primitif. Le corps de décomposition est un ensemble de cardinal pδ. Son groupe multiplicatif est un groupe cyclique d'ordre pδ -1. L'analyse des groupes cycliques montre que ce groupe contient les racines n-ième de l'unité si et seulement si son cardinal est un multiple de n. En conséquence δ est égal à l'ordre multiplicatif de p modulo n, c’est-à-dire le plus petit entier δ tel que pδ-1 soit un multiple de n.

  • Un polynôme cyclotomique d'indice n sur Fp est de degré l'ordre multiplicatif de p modulo n.

Le théorème d'Euler montre que:

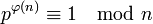
p^{\varphi(n)} \equiv 1 \mod n

Cependant, l'ordre multiplicatif de p modulo n est égal à φ(n) si et seulement si n - 1 n'est pas un multiple de p. Dans l'exemple précédent, p est égal à 2, n à sept, φ(n) égale six, un multiple de p. Le théorème d'Euler est bien vérifié car soixante quatre est congru à un modulo sept, mais l'ordre multiplicatif est égal à trois car huit est congru à un modulo sept.

  • Si δ désigne l'ordre multiplicatif de p modulo n, il existe φ(n)/δ polynômes cyclotomiques d'indice n sur Fp. Leur degré est égal à δ et leur produit est l'image du polynôme cyclotomique d'indice n à coefficients dans Z par le morphisme canonique de Z[X] dans Fp[X].

Des exemples sont donnés dans l'article corps fini.

Extension cyclotomique

L'extension cyclotomique est par définition le corps de rupture d'un polynôme cyclotomique, c’est-à-dire le plus petit corps contenant une racine primitive n-ième d'un polynôme cyclotomique. (Rappelons qu'un corps de rupture d'un polynôme est une extension de corps permettant une factorisation de ce polynôme.) Il possède des propriétés fortes, à l'origine de nombreuses applications:

  • L'extension cyclotomique est un espace vectoriel sur le corps des nombres rationnels de dimension φ(n).

Cette propriété est générale aux corps de ruptures. La démonstration est donnée dans l'article Extension algébrique.

Cela signifie que le plus petit corps contenant une racine du polynôme contient aussi toutes les racines du polynôme. Dire que ce corps est une extension galoisienne signifie deux choses: d'une part, les polynômes minimaux de ce corps n'ont pas de racines multiples (ce qui est toujours vraie pour les extensions sur les nombres rationnels) ; et d'autre part, tous les morphismes de ce corps dans les nombres complexes ont pour image le corps lui-même. Ce sont donc des automorphismes. Ils forment une structure de groupe appelé groupe de Galois. La théorie de Galois indique que c'est la bonne structure pour rechercher une expression des racines par radicaux.

Cela signifie que le groupe de Galois est commutatif (ou abélien). L'équation polynomiale cyclotomique est alors résoluble par radicaux. Autrement dit, les solutions s'expriment à l'aide des uniques quatre opérations (additionner, soustraire, diviser et multiplier) et des racines p-ième appliquées un nombre fini de fois sur des nombres rationnels et l'imaginaire pure i. Ce résultat est connu sous le nom de théorème d'Abel. Il est ainsi possible par exemple de résoudre par radicaux l'équation cyclotomique donnant la racine dix-septième de l'unité. C'est une condition nécessaire pour la résolution de la construction par la règle et le compas du polygone régulier à dix-sept cotés (voir ci-dessous).

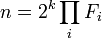
n=2^k \prod_iF_i\;
Où les Fi sont des nombres premiers de Fermat distincts.

Ce résultat est aussi connu sous le nom de Théorème de Gauss-Wantzel. Une tour d'extension quadratique est un corps tel que pour chaque élément x du corps, il existe une suite de sous-corps K0, K1, ..., Kp avec K0 égal au corps de base, ici celui des rationnels, Kp contient x, et, pour tout i entre 1 et p, Ki contient Ki - 1 et est un espace vectoriel de dimension 2 sur Ki - 1.

Dire que Ki contient Ki - 1 et est un espace vectoriel de dimension 2 sur Ki - 1 revient seulement à dire que tout élément de Ki s'exprime comme la somme d'un nombre de Ki - 1 et d'une racine carré d'un nombre de Ki - 1. En particulier, tout élément de Ki s'exprime comme racine d'un polynôme de degré 2 sur Ki-1. Cette propriété est démontrée dans l'article Extension quadratique.

Or l'article sur les nombres constructibles montre qu'un point est constructible si et seulement s'il vérifie cette propriété. Cette propriété permet donc de déterminer la liste des polygones constructibles et assure qu'ils le sont effectivement.

Un nombre premier de Fermat est un nombre premier de la forme 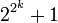2^{2^k} + 1 où k est un entier. Les nombres premiers de Fermat connus sont 3, 5, 17, 257 et 65 537.


Démonstrations
  • L'extension cyclotomique est aussi le corps de décomposition du polynôme. Elle est donc une galoisienne.

L'extension contient z et donc toutes ses puissances, or les puissances de z forment l'ensemble des racines n-ièmes de l'unité et donc en particulier les racines primitives qui sont les racines du polynôme cyclotomique. Ceci démontre que Q[z] est le corps de décomposition. Dans un corps parfait comme celui des rationnels (un corps parfait est un corps où tous les polynômes irréductibles sont séparables c’est-à-dire n'ont pas de racines multiples dans la clôture algébrique) un corps de décomposition est toujours une extension de Galois.

  • L'extension cyclotomique est abélienne.

Soit d un entier plus petit que n et qui ne divise pas n. Alors zd est une racine du polynôme cyclotomique et il existe au moins un morphisme qui envoie z sur zd (cf première proposition du paragraphe Extension algébrique et sur-corps). Il n'existe qu'un unique moyen de prolonger sur l'extension le morphisme md qui à z associe zd. En effet md(zi) = md(z)i = z i.d. Or la famille des z i si i varie de 0 à φ(n) - 1 forme une base de l'extension. Les automorphismes du groupe de Gallois sont donc parfaitement déterminés.

Considérons alors l'application du groupe multiplicatif des éléments inversibles de 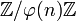\mathbb{Z} / \varphi(n)\mathbb{Z} du groupe de Galois qui, à la classe de d associe l'automorphisme md. Cette application est clairement un isomorphisme de groupe. Cet isomorphisme montre que le groupe de Galois est abélien, et même cyclique, ce qui termine la démonstration.

  • Condition nécessaire pour que l'extension soit une tour d'extension quadratique.

Par définition d'une tour d'extension quadratique, une condition nécessaire est que la dimension de l'extension soit une puissance de deux. Étudions alors les entiers n tel que φ(n) soit une puissance de deux.

Remarquons tout d'abord que si n est égal à p.q avec p et q premiers entre eux alors nous avons l'égalité suivante φ(n) = φ(p).φ(q) (cf l'article Indicatrice d'Euler). Considérons alors la décomposition de n en facteur premier (cf l'article Théorème fondamental de l'arithmétique).

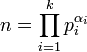
n= \prod_{i=1}^k p_i^{\alpha_i}\;

L'indicatrice d'Euler d'une puissance d'un nombre premier pα est égale à (p - 1). pα -1. Il suffit donc de trouver une condition nécessaire et suffisante pour que le facteur (p - 1). pα -1 soit une puissance de deux et appliquer cette condition à chacun des facteurs de l'égalité précédente. Deux cas se présentent, soit p est égal à 2 et toute valeur de α est acceptable, soit p est un nombre premier de la forme 2k + 1 avec k un entier strictement positif et α est égal à 1.

Montrons par contraposé que si p est un nombre premier de la forme 2k + 1 alors k est une puissance de deux. Si tel n'est pas le cas, alors il existe deux entiers a et b tel que k = a . 2b où a est un entier impair et b un entier. L'égalité suivante est vérifiée p = 1 + ca ou c = 2b. Dans ce cas, comme a est impair, on a l'égalité:

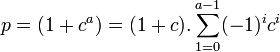
p = (1 + c^a) = (1 + c). \sum_{1=0}^{a-1} (-1)^i c^i\;

L'égalité précédente montre que 1 + c est un diviseur de p. Par contraposé, si p est premier, il est donc égal à un nombre de Fermat.

En conclusion n est de la forme suivante:

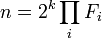
n=2^k \prod_iF_i\;

Où les Fi sont des nombres premiers de Fermat distincts. Et la condition nécessaire est démontrée.

  • Condition suffisante pour que l'extension soit une tour d'extension quadratique.

Le polynôme cyclotomique est alors de degré φ(n) et est une puissance de deux. Notons 2k ce degré. Le groupe de Galois est alors le groupe cyclique de cardinal 2k.

Montrons que si l est un entier inférieur à k il existe un sous-groupe Gl du groupe cyclique de cardinal 2l et tel que si l est non nul alors Gl - 1 est inclus dans Gl. Définissons Gl comme le sous-groupe engendré par la classe de 2k-l. Par définition Gl - 1 est inclus dans Gl si l est non nul. De plus le cardinal de Gl est clairement égal à 2k-l.

On remarque ensuite que Gl-1 est un sous-groupe distingué de Gl car ce sont des groupes abéliens, donc tout sous-groupe est distingué. Ensuite le cardinal du groupe quotient de Gl par Gl - 1 est deux.

Le théorème fondamental de la théorie de Galois assure que si Kk- l est le sous-corps de l'extension qui laisse invariant tous les automorphismes de Gl (on a ici identifié le groupe de Galois et le groupe cyclique) alors si l est non nul Kl est une extension galoisienne de Kl - 1 de dimension deux donc quadratique, que K0 est égal au corps des nombres rationnels et que Kk est le corps de décomposition du polynôme cyclotomique.

Nous avons donc monté une tour d'extension quadratique du corps de décomposition et le théorème est démontré.

Applications

Théorème de Wedderburn

Article détaillé : théorème de Wedderburn.
Wederburn schema 2.jpg

Le théorème de Wedderburn affirme que tout corps fini K est nécessairement commutatif. La démonstration usuelle est relativement curieuse. Tout d'abord le polynôme cyclotomique utilisé est celui de la caractéristique zéro et non celui du corps. Ensuite, son rôle est celui d'un dénombrement. Le raisonnement est par l'absurde, les cardinaux des classes par l'action par conjugaison sont sommés pour obtenir le cardinal du groupe multiplicatif du corps. Cette égalité s'exprime par une expression du type:

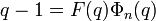q-1=F(q)\Phi_n(q)\;,

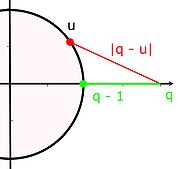
La valeur q est celle du centre du groupe multiplicatif de K plus 1 correspondant au point zéro, F[X] est un polynôme à coefficients entiers. Ce qui implique que F[q] est une valeur entière. La fin de la démonstration quitte le dénombrement pour devenir géométrique. Si l'égalité précédente, est vraie, alors il existe une racine primitive n-ième de l'unité u vérifiant la majoration suivante:

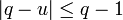
|q-u|\le q-1

Comme q - 1 est le cardinal du centre du groupe commutatif q est au moins égal à 2. La figure de droite démontre l'impossibilité. La démonstration détaillée est donnée dans l'article associé.

Polygone constructible

Cas du pentagone

Construction d'un pentagone
Article détaillé : Construction du pentagone régulier à la règle et au compas.

Si la théorie de Galois prend un aspect quelque peu abstrait, elle donne néanmoins une méthode de résolution effective de l'équation cyclotomique et en conséquence propose un mode de construction à la règle et au compas des polygones constructibles (cf l'article nombre constructible). Étudions le pentagone à cinq cotés.

A une similitude directe près du plan euclidien, les sommets du pentagone régulier sont exactement les cinq racines cinquièmes de l'unité. Par identification, ils sont, hormis 1, les racines du cinquième polynôme cyclotomique, soit donc :

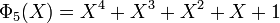
\Phi_5(X) = X^4 + X^3 + X^2 + X + 1\,

.

Si l'équation correspondante est un polynôme du quatrième degré, elle est néanmoins résoluble avec une quantité de calcul faible. Le corps de décomposition, noté parfois F5, est (par oubli de structure) un espace vectoriel rationnel de dimension quatre. Son groupe de Galois G est le groupe cyclique d'ordre quatre. Il admet donc un générateur noté ici m et un sous-groupe non trivial H, contenant deux éléments, l'identité et m2. L'application qui à tout élément de l'extension associe son conjugué est un automorphisme qui laisse F5 stable, Q invariant et est d'ordre deux ; en conséquence m2 est précisément l'application conjuguée. L'objectif est donc de trouver le sous-corps de F5 de dimension deux sur Q, laissant ses éléments invariants par l'application conjuguée. Un jeu de permutation des racines permet alors de ramener la résolution de l'équation à trois équations simples du second degré.

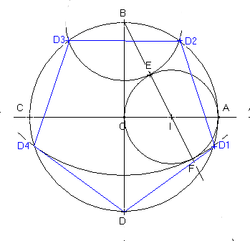
Il est alors relativement simple d'obtenir une construction à la règle et au compas. Sur la figure illustrative, il est par exemple immédiat de remarquer que la longueur du segment BI est la moitié de la racine carrée de cinq, le radical de la première extension.


Calcul
Comme ci-dessus, z désigne la racine primitive cinquième privilégiée, à savoir exp(i.2.pi/5) et le générateur m du groupe de Galois est l'automorphisme sur Q de l'extension F5 uniquement défini par l'identité :
m(z) = z2
.
Déterminons les éléments de F5 laissés invariants par la conjugaison complexe m2. Or, m2(z)= z4 ; m2(z2)=z3 ; et enfin m2 est d'ordre deux. Donc u = z + z4 et son image v = m(u) = z2 + z3 sont clairement invariants par m2. De plus, leur somme u+v et leur produit u.v sont invariants par m et donc par le groupe de Galois ; on s'attend à ce qu'ils soient donc rationnels. La somme u+v est la somme des quatre racines cinquièmes et vaut donc -1 ; le produit est aussi égal à la somme des racines cinquièmes primitives, soit -1.
On en déduit que u et v vérifie l'équation P[X] = 0 où:
P[X] = X^2 + X - 1 =0 \quad et \quad u = \frac{1}{2} (-1 + \sqrt{5}) \quad v = \frac{1}{2} (-1 - \sqrt{5})
Ces formules auraient pu être démontrées en remarquant que z4 est le conjugué de z. Il en est de même avec z2 et z3.
En effet, on a :
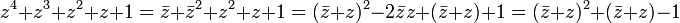
z^4 + z^3 + z^2+ z+1 = \bar{z}+\bar{z}^2 + z^2 + z + 1 = (\bar{z} + z)^2 -2\bar{z}z + (\bar{z} + z)+ 1 = (\bar{z} + z)^2 + (\bar{z} + z)- 1
Avec :
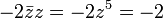
-2\bar{z}z=-2z^5=-2
Et le carré du conjugué est égal au conjugué du carré de z.
L'ensemble des points fixes par m2, donc par H forment une extension intermédiaire de Q, notée habituellement F5H. Le polynôme Φ5[X] se factorise dans l'algèbre F5H[X] comme suit:
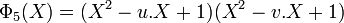
\Phi_5(X) = (X^2 -u.X + 1)(X^2 -v.X + 1)\,
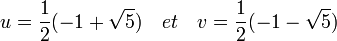
u = \frac{1}{2} (-1 + \sqrt{5}) \quad et \quad v = \frac{1}{2} (-1 - \sqrt{5})

Et dans F5[X], le polynôme prend la forme:

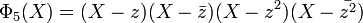
\Phi_5(X) = (X - z)(X - \bar{z})(X - z^2)(X - \bar{z^2})\,
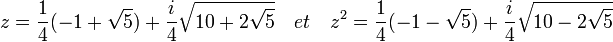
z = \frac{1}{4} (-1 + \sqrt{5})+ \frac{i}{4} \sqrt{10 + 2\sqrt{5}} \quad et \quad z^2 = \frac{1}{4} (-1 - \sqrt{5})+ \frac{i}{4} \sqrt{10 - 2\sqrt{5}}
.

Cas de l'heptadécagone

Figure à la règle et au compas: Heptadécagone, le polygone régulier de 17 cotés

Le nombre premier de Fermat suivant est dix-sept. Il correspond à l'heptadécagone, le polygone régulier à dix-sept cotés. Si la logique précédente s'applique avec le même succès, les calculs sont néanmoins plus complexes. Le polynôme à factoriser est maintenant de degré seize. En conséquence, ce cas n'a pas été traité avant une compréhension profonde des polynômes cyclotomiques. L'aspect calculatoire de la résolution du problème est indéniable, en rechange il relativement limité pour une équation de degré seize sans racine évidente ou multiple.

La méthode de résolution proposée ici suit pas à pas la démarche de la théorie de Galois. Ce groupe est le groupe cyclique d'ordre seize. Il contient donc trois sous-groupes non triviaux. H1 est un sous-groupe à huit éléments, il contient les multiples de deux, H2 contient les multiples de quatre et H3 contient deux éléments le neutre et le multiple de huit, la même remarque que celle du paragraphe précédent montre que l'élément non neutre correspond à l'application conjuguée. Les sous-corps associés forment une chaîne d'extensions strictement emboitée tel que la dimension d'un corps est deux sur le corps précédent.

\mathbb{Q} \sub \mathbb{F}_{17}^{H_1} \sub \mathbb{F}_{17}^{H_2} \sub \mathbb{F}_{17}^{H_3} \sub \mathbb{F}_{17}\;

L'objectif est alors de trouver un générateur de chaque extension dans la précédente. La technique utilisé dite des périodes de Gauss est toujours la même. Explicitons la pour la première extension. Soit m2 le générateur du premier groupe (on a choisi m générateur du groupe de Galois), Considérons la somme des huit composées successives de z la première racine primitive, et la somme des huit autres racines:

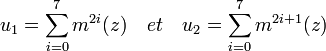
u_1=\sum_{i=0}^7 m^{2i}(z)\quad et \quad u_2=\sum_{i=0}^7 m^{2i+1}(z)\;

Alors ces deux éléments sont invariant par le générateur m2. De plus, leur somme est égal à -1 car c'est la somme de toutes les racines primitives. Ils sont donc de la forme u1 = a + b.r et u2 = a - b.r où a et b sont des rationnels et r le radical générateur de l'extension, car nous sommes dans une extension quadratique. Leur produit est donc encore rationnel. On en déduit une équation du type P1[X] = 0 avec P1[X] un polynôme du deuxième degré.

Réitérer trois fois cette méthode donne alors la solution.


Calcul

Choisir m tel que m(z) = z2 n'est pas la solution car m est d'ordre huit. Il est donc plus judicieux de choisir m tel que m(z) = z3 m et m2 restreints aux racines sont donc deux permutations décrites par:

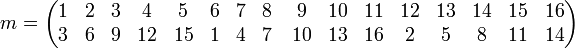
m= \left( \begin{matrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ 3 & 6 & 9 & 12 & 15 & 1 & 4 & 7 \end{matrix} \quad \begin{matrix} 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16 \\ 10 & 13 & 16 & 2 & 5 & 8 & 11 & 14 \end{matrix}\right)
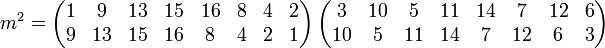
m^2= \left( \begin{matrix} 1 & 9 & 13 & 15 & 16 & 8 & 4 & 2 \\ 9 & 13 & 15 & 16 & 8 & 4 & 2 & 1 \end{matrix} \right) \left( \begin{matrix} 3 & 10 & 5 & 11 & 14 & 7 & 12 & 6 \\ 10 & 5 & 11 & 14 & 7 & 12 & 6 & 3 \end{matrix}\right)

Alors u1 est la somme des racines de puissance: 1 ,9 ,13 ,15, 16, 8, 4, 2 et u2 les autres. Leur somme est égale à la somme des racines donc -1 et leur produit à quatre fois la somme des racines donc -4. On obtient:

P_1[X]=X^2+X -4=0 \quad et \quad u_1 = \frac{1}{2}(-1 + \sqrt{17}) \quad u_2 = \frac{1}{2}(-1 - \sqrt{17}))\,

Pour appliquer cette même logique une deuxième fois déterminons m4 :

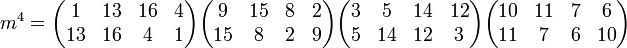
m^4 = \begin{pmatrix} 1 & 13 & 16 & 4 \\ 13 & 16 & 4 & 1 \end{pmatrix} \begin{pmatrix} 9 & 15 & 8 & 2 \\ 15 & 8 & 2 & 9 \end{pmatrix} \begin{pmatrix} 3 & 5 & 14 & 12 \\ 5 & 14 & 12 & 3 \end{pmatrix} \begin{pmatrix} 10 & 11 & 7 & 6 \\ 11 & 7 & 6 & 10 \end{pmatrix}

Notons alors v1 la somme des racines d'exposant 1, 13, 16, 4 notons v2 la somme des racines d'exposant 2, 9, 15, 8 notons v3 la somme des racines d'exposant 3, 5, 14, 12 et v4 la somme des racines d'exposant 10, 11, 7, 6

P_2[X]=X^2-u_1X -1=0 \quad et \quad v_1 = \frac{1}{2}(u_1 + \sqrt{4+u_1^2}) \quad v_2 = \frac{1}{2}(u_1 - \sqrt{4+u_1^2})\,
P'_2[X]=X^2-u_2X -1=0 \quad et \quad v_3 = \frac{1}{2}(u_2 + \sqrt{4+u_2^2}) \quad v_4 = \frac{1}{2}(u_2 - \sqrt{4+u_2^2})\,

Le calcul effectif donne:

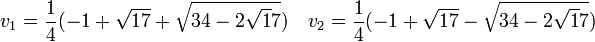
v_1 = \frac{1}{4}(-1 + \sqrt{17}+\sqrt{34-2\sqrt17}) \quad v_2 = \frac{1}{4}(-1 + \sqrt{17}-\sqrt{34-2\sqrt17})
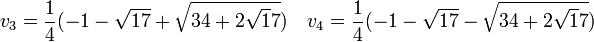
v_3 = \frac{1}{4}(-1 - \sqrt{17}+\sqrt{34+2\sqrt17}) \quad v_4 = \frac{1}{4}(-1 - \sqrt{17}-\sqrt{34+2\sqrt17}) \,

L'étape suivante ne demande pas la détermination de m8 car il est établi que cette application est le conjugué, à une racine d'exposant i elle associe donc la racine d'exposant 17 - i. On choisit alors w1 comme la somme des racines d'exposant 1 et 16 et w2 comme la somme des racines d'exposant 13 et 4. On obtient:

P_3[X]=X^2-v_1X +v_3=0 \quad et \quad w_1 = \frac{1}{2}(v_1 + \sqrt{v_1^2-4v_3})\,
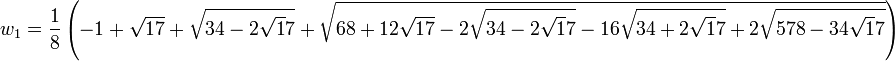
w_1 = \frac{1}{8}\left(-1 + \sqrt{17}+\sqrt{34-2\sqrt17} +\sqrt{68 +12\sqrt{17}-2\sqrt{34-2\sqrt17}-16\sqrt{34+2\sqrt17}+2\sqrt{578-34\sqrt17}}\right)\,

Le calcul de w1 suffit pour obtenir la racine primitive. On sait par construction que ce coefficient est égal à la somme de la première racine primitive et de son conjugué. On en déduit alors que:

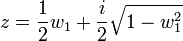
z = \frac{1}{2}w_1+\frac{i}{2}\sqrt{1-w_1^2}\,

La construction à la règle et au compas est moins douloureuse qu'il n'y paraît, u1 a pour radical une longueur égal à l'hypoténuse d'un triangle de côté un et un quart. u2 a pour radical l'hypoténuse d'un triangle de côté 2 et u1. Seule l'étape suivante est un peu pénible. Un développement brutal laisserait en effet à penser à une construction plus délicate. Il donne.

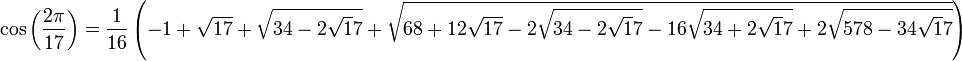
\cos\left(\frac{2\pi}{17}\right) = \frac{1}{16}\left(-1 + \sqrt{17}+\sqrt{34-2\sqrt17} +\sqrt{68 +12\sqrt{17}-2\sqrt{34-2\sqrt17}-16\sqrt{34+2\sqrt17}+2\sqrt{578-34\sqrt17}}\right)\,

Voir aussi

Notes

  1. ↑ Pierre-Laurent Wantzel, Recherches sur les moyens de reconnaître si un problème de Géométrie peut se résoudre avec la règle et le compas, 1837
  2. ↑ Al-Khawarizmi, Abrégé du calcul par la restauration et la comparaison
  3. ↑ Gerolamo Cardano, Ars Magna, 1545.
  4. ↑ Joseph-Louis Lagrange, Réflexions sur la résolution algébrique des équations, 1770
  5. ↑ Paolo Ruffini, La théorie générale des équations dans laquelle il est démontré qu'il est impossible de donner les solutions générales des équations de degré strictement supérieur à 4, 1799
  6. ↑ Niels Henrik Abel, Mémoire sur les équations algébriques, où l'on démontre l'impossibilité de la résolution de l'équation générale du cinquième degré, 1824.
  7. ↑ Évariste Galois, Manuscrit de Galois dans Journal des mathématiques pures et appliquées, 1846
  8. ↑ Heinrich Weber, Lecture en algèbre, 1895
  9. ↑ David Hilbert, La théorie des corps de nombres algébriques, 1897.
  10. ↑ Emil Artin, Beweis des allgemeinen Reziprozitätsgesetzes, 1927
  11. ↑ Ferdinand Georg Frobenius, Sur le caractère du groupe Académie de Berlin 1896
  12. ↑ Leonard Dickson Linear Groups With an Exposition of the Galois Field Theory 1901

Liens externes

Références

  • JP Escofier Théorie de Galois. Cours avec exercices corrigés Masson Paris, 1997
  • Serge Lang, Algèbre, Dunod, 2004, 926 p. (ISBN 2100079808) [détail des éditions]
  • Pierre Samuel, Théorie algébrique des nombres [détail des éditions]
Articles de mathématiques en rapport avec la théorie de Galois
Corps Corps fini · Corps parfait · Corps de rupture · Corps de décomposition
Extension de corps Extension algébrique · Extension quadratique · Extension simple · Extension normale · Extension séparable · Extension de Galois · Groupe de Galois · Clôture algébrique
Articles associés Caractéristique · Polynôme formel · Polynôme cyclotomique · Théorie de Galois · Théorème fondamental de la théorie de Galois · Théorème de l'élément primitif · Théorie d'Iwasawa
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Polyn%C3%B4me cyclotomique ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Polynome cyclotomique de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Polynôme cyclotomique — Carl Friedrich Gauss En mathématiques, plus précisément en algèbre commutative, le polynôme cyclotomique[1] usuel associé à un entier naturel n est le polynôme unitaire dont les racine …   Wikipédia en Français

  • Polynome — Polynôme Courbe polynomiale cubique Un polynôme, en mathématiques, est la combinaison linéaire des produits de puissances d une ou de plusieurs indéterminées, habituellement notées X, Y, Z… Ces objets sont largement utilisés en pratique, ne… …   Wikipédia en Français

  • Polynome minimal d'un nombre algebrique — Polynôme minimal d un nombre algébrique Carl Friedrich Gauß utilise des polynômes minimaux appelés cyclotomiques pour déterminer les polygones constructibles à la règle et au compas. En mathématiques, le polynôme minimal d un nombre algébrique… …   Wikipédia en Français

  • Polynôme —  Ne doit pas être confondu avec Polygone. Courbe polynomiale cubique Un polynôme, en mathématiques, est une expression formée d une combinaison linéaire de produits d …   Wikipédia en Français

  • Polynôme formel — En algèbre, le terme de polynôme formel, ou simplement polynôme, est le nom générique donné aux éléments d une structure construite à partir d un ensemble de nombres. On considère un ensemble A de nombres, qui peut être celui des entiers ou des… …   Wikipédia en Français

  • Polynôme minimal d'un nombre algébrique —  Ne doit pas être confondu avec Polynôme minimal d un endomorphisme. Carl Friedrich Gauß utilise des polynômes minimaux appelés cyclotomiques pour déter …   Wikipédia en Français

  • Extension cyclotomique — En théorie algébrique des nombres, on appelle extension cyclotomique du corps Q des nombres rationnels tout corps de rupture d un polynôme cyclotomique, i.e. tout corps de la forme Q(ζ) où ζ est une racine de l unité. Ces corps jouent un rôle… …   Wikipédia en Français

  • Division d'un polynôme — En algèbre, l anneau K[X] des polynôme à une indéterminée X et à coefficients dans un corps commutatif K, comme celui des nombres rationnels, réels ou complexes, dispose d une division euclidienne, qui ressemble formellement à celle des nombres… …   Wikipédia en Français

  • Algèbre polynomiale — Polynôme Courbe polynomiale cubique Un polynôme, en mathématiques, est la combinaison linéaire des produits de puissances d une ou de plusieurs indéterminées, habituellement notées X, Y, Z… Ces objets sont largement utilisés en pratique, ne… …   Wikipédia en Français

  • Polynomial — Polynôme Courbe polynomiale cubique Un polynôme, en mathématiques, est la combinaison linéaire des produits de puissances d une ou de plusieurs indéterminées, habituellement notées X, Y, Z… Ces objets sont largement utilisés en pratique, ne… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”