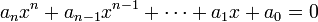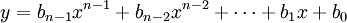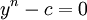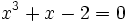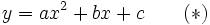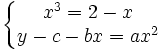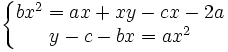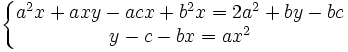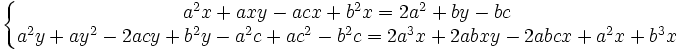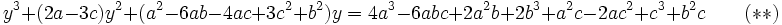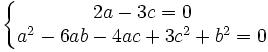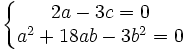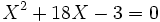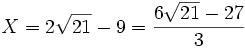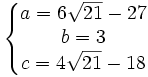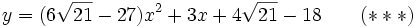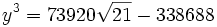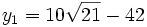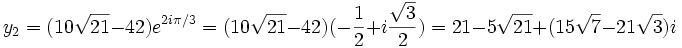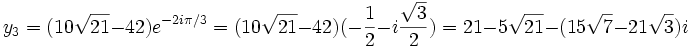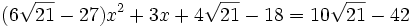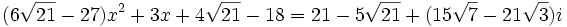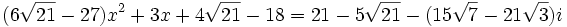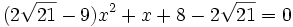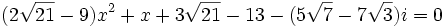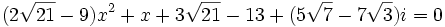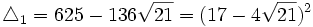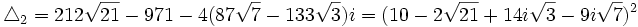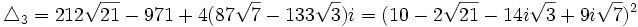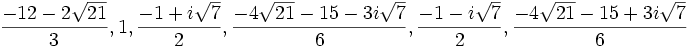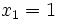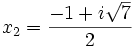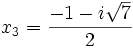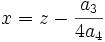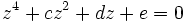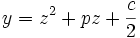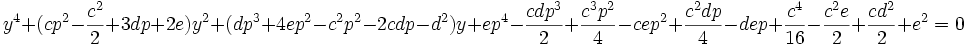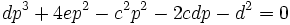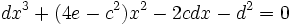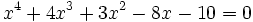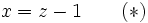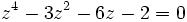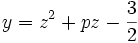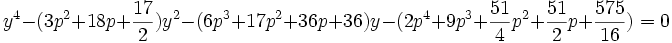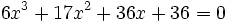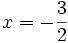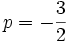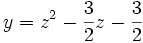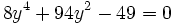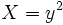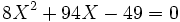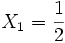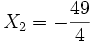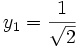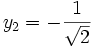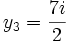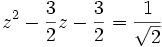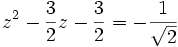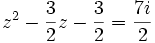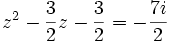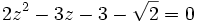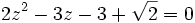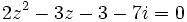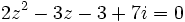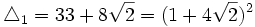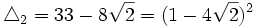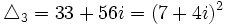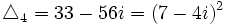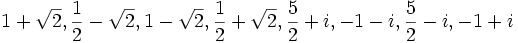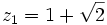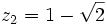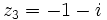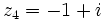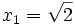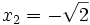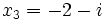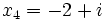Methode de Tschirnhaus

Méthode de Tschirnhaus

La méthode de Tschirnhaus, imaginée et mise au point par Ehrenfried Walther von Tschirnhaus, est une tentative de résoudre le point clé de la théorie des équations à savoir trouver une méthode générale de résolution de l'équation polynomiale. Cette méthode tente de ramener l'équation que l'on veut résoudre à d'autres équations de degré moins élevé. Cette méthode échoue de façon certaine pour les équations de degré supérieur ou égal à cinq qui ont un groupe de Galois non résoluble.

Sommaire

1 Principe de la méthode
2 Application à la résolution des équations cubiques
3 Méthode particulière pour les équations du quatrième degré
4 Equation du cinquième degré
5 Remarque historique
6 Autres méthodes de résolution d'équations

Principe de la méthode

Considérons une équation de degré n :

$\qquad a_n x^n + a_{n - 1} x^{n - 1} + \cdots + a_1 x + a_0 = 0$

Le principe de la méthode consiste à faire un changement de variable en posant :

$\qquad y = b_{n-1}x^{n-1}+b_{n-2}x^{n-2}+\cdots+b_1 x + b_0$

Une transformation de ce type se nomme transformation de Tschirnhaus.

En éliminant x entre cette relation et l'équation à résoudre, on obtient une équation de degré n et d'inconnue y dont les coefficients dépendent de 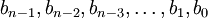$b_{n-1}, b_{n-2}, b_{n-3}, \ldots, b_1, b_0\,$ . On va alors essayer de déterminer 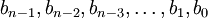$b_{n-1}, b_{n-2}, b_{n-3}, \ldots, b_1, b_0\,$ de façon à obtenir une équation en y plus simple à résoudre, par exemple de la forme :

$\qquad y^n - c = 0$

Pour cela, dans l'équation en y, on pose égal à 0, tous les coefficients des monômes de degré 1 à n-1. On obtient ainsi un système de n-1 équations à n inconnues 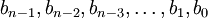$b_{n-1}, b_{n-2}, b_{n-3}, \ldots, b_1, b_0\,$ . Ces valeurs, une fois obtenues, sont reportées dans la relation :

$\qquad y = b_{n-1}x^{n-1}+b_{n-2}x^{n-2}+\cdots+b_1 x + b_0$

Où y prendra successivement pour valeur l'une des n racines de c.

Nous nous sommes donc ramené à la résolution de n équations en x de degré n-1. Nous pouvons renouveler ainsi l'opération jusqu'à obtenir des équations de degré suffisamment bas pour pouvoir les résoudre.

Application à la résolution des équations cubiques

Nous allons exposer la méthode sur l'exemple suivant :

$x^3+x-2=0 ~$

Posons :

$y = ax^2+bx+c \qquad (*)~$

Les deux équations précédentes se mettent sous la forme :

$\left\{\begin{matrix} x^3=2-x \\ y-c-bx=ax^2 \end{matrix}\right.$

Nous devons éliminer x entre ces deux équations. Pour cela, nous remplaçons la première équation par le produit membre à membre de ces deux équations. Après simplification, nous obtenons :

$\left\{\begin{matrix} bx^2=ax+xy-cx-2a \\ y-c-bx=ax^2 \end{matrix}\right.$

Cette façon de procéder permet de diminuer le degré de l'une des équations par rapport à x. Nous allons donc réitérer le processus jusqu'à ce que x ait disparu de l'une des équations. D'autre part, comme nous faisons des produits membre à membre, nous risquons d'introduire des solutions parasites. Il nous sera donc nécessaire à la fin de la résolution de vérifier que toutes les solutions trouvées vérifient bien l'équation à résoudre.

Après un nouveau produit membre à membre, nous obtenons :

$\left\{\begin{matrix} a^2x+axy-acx+b^2x=2a^2+by-bc \\ y-c-bx=ax^2 \end{matrix}\right.$

Après un nouveau produit membre à membre en remplaçant cette fois la deuxième équation, nous obtenons :

$\left\{\begin{matrix} a^2x+axy-acx+b^2x=2a^2+by-bc \\ a^2y+ay^2-2acy+b^2y-a^2c+ac^2-b^2c=2a^3x+2abxy-2abcx+a^2x+b^3x \end{matrix}\right.$

Un dernier produit membre à membre nous donne après réduction des termes semblables et simplification par a²x :

$y^3+(2a-3c)y^2+(a^2-6ab-4ac+3c^2+b^2)y=4a^3-6abc+2a^2b+2b^3+a^2c-2ac^2+c^3+b^2c \qquad (**) ~$

Nous devons maintenant déterminer a, b, c de façon à ce que :

$\left\{\begin{matrix} 2a-3c=0 \\ a^2-6ab-4ac+3c^2+b^2=0 \end{matrix}\right.$

En tirant c de la première équation et en reportant dans la deuxième équation, nous obtenons :

$\left\{\begin{matrix} 2a-3c=0 \\ a^2+18ab-3b^2=0 \end{matrix}\right.$

Nous voyons alors que le rapport a/b est racine de l'équation :

$X^2+18X-3=0 ~$

L'une des racines de cette équation étant :

$X=2\sqrt{21}-9=\frac{6\sqrt{21}-27}{3} ~$

On peut en déduire pour a, b, c le choix des valeurs suivantes :

$\left\{\begin{matrix} a=6\sqrt{21}-27 \\ b=3 \\ c=4\sqrt{21}-18 \end{matrix}\right.$

En reportant ces valeurs d'une part dans (*), on obtient :

$y = (6\sqrt{21}-27 )x^2+3x+4\sqrt{21}-18 \qquad (***)~$

Et d'autre part dans (**), on obtient :

$y^3=73920\sqrt{21}-338688 ~$

D’où l'on déduit les trois valeurs possibles de y :

$y_1=10\sqrt{21}-42 ~$

$y_2= (10\sqrt{21}-42)e^{2i\pi/3} = (10\sqrt{21}-42)(-\frac{1}{2}+i\frac{\sqrt{3}}{2}) = 21-5\sqrt{21} + (15\sqrt{7}-21\sqrt{3})i ~$

$y_3=(10\sqrt{21}-42)e^{-2i\pi/3} = (10\sqrt{21}-42)(-\frac{1}{2}-i\frac{\sqrt{3}}{2}) = 21-5\sqrt{21} - (15\sqrt{7}-21\sqrt{3})i~$

Il nous suffit de reporter ces trois valeurs de y dans (***) pour obtenir successivement les trois équations du second degré suivantes :

$(6\sqrt{21}-27 )x^2+3x+4\sqrt{21}-18 = 10\sqrt{21}-42 ~$

$(6\sqrt{21}-27 )x^2+3x+4\sqrt{21}-18 = 21-5\sqrt{21} + (15\sqrt{7}-21\sqrt{3})i ~$

$(6\sqrt{21}-27 )x^2+3x+4\sqrt{21}-18 = 21-5\sqrt{21} - (15\sqrt{7}-21\sqrt{3})i ~$

Qui se simplifient sous la forme :

$(2\sqrt{21}-9 )x^2+x+8-2\sqrt{21} = 0 ~$

$(2\sqrt{21}-9 )x^2+x+3\sqrt{21}-13-(5\sqrt{7}-7\sqrt{3})i = 0 ~$

$(2\sqrt{21}-9 )x^2+x+3\sqrt{21}-13+(5\sqrt{7}-7\sqrt{3})i = 0 ~$

Il ne nous reste plus qu'à résoudre ces trois équations pour en déduire les valeurs possibles de x. Les trois discriminants de ces équations du second degré sont respectivement :

$\triangle_1 = 625-136\sqrt{21} = (17-4\sqrt{21})^2 ~$

$\triangle_2 = 212\sqrt{21} - 971 - 4(87\sqrt{7}-133\sqrt{3})i = (10-2\sqrt{21}+14i\sqrt{3}-9i\sqrt{7})^2 ~$

$\triangle_3 = 212\sqrt{21} - 971 + 4(87\sqrt{7}-133\sqrt{3})i = (10-2\sqrt{21}-14i\sqrt{3}+9i\sqrt{7})^2 ~$

On en déduit respectivement les six valeurs possibles pour x :

$\frac{-12-2\sqrt{21}}{3}, 1 ,\frac{-1+i\sqrt{7}}{2}, \frac{-4\sqrt{21}-15-3i\sqrt{7}}{6},\frac{-1-i\sqrt{7}}{2}, \frac{-4\sqrt{21}-15+3i\sqrt{7}}{6} ~$

Comme nous avons fait des produits membre à membre au début, nous risquons d'avoir introduit des racines parasites. Nous devons donc vérifier que les valeurs obtenues pour x vérifient bien l'équation à résoudre. Nous constatons que seulement trois des six valeurs obtenues sont bien solution de l'équation. Ces valeurs sont :

$x_1 = 1 ~$

$x_2 = \frac{-1+i\sqrt{7}}{2} ~$

$x_3 = \frac{-1-i\sqrt{7}}{2} ~$

Méthode particulière pour les équations du quatrième degré

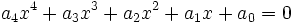
Considérons l'équation générale du quatrième degré suivante : $\qquad a_4 x^4 + a_3 x^3 + a_2 x^2 + a_1 x + a_0 = 0$

En divisant par 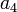$a_4\,$ et en posant

$\qquad x = z - \frac{a_3}{4a_4}$

on se ramène à une équation de la forme :

$\qquad z^4 + c z^2 + d z+ e = 0$

Considérons la transformation de Tschirnhaus suivante :

$y = z^2 + pz + \frac{c}{2} ~$

En éliminant z entre les deux relations précédentes, nous obtenons l'équation du quatrième degré en y suivante :

$y^4 + (cp^2-\frac{c^2}{2}+3dp+2e)y^2 + (dp^3+4ep^2-c^2p^2-2cdp-d^2)y + ep^4-\frac{cdp^3}{2}+\frac{c^3p^2}{4}-cep^2+\frac{c^2dp}{4}-dep+\frac{c^4}{16}-\frac{c^2e}{2}+\frac{cd^2}{2}+e^2 = 0 ~$

Nous voyons alors que nous pouvons obtenir à ce niveau une équation bicarrée du quatrième degré si p vérifie la relation :

$dp^3+4ep^2-c^2p^2-2cdp-d^2 = 0~$

C'est-à-dire si p est solution de l'équation du troisième degré:

$dx^3+(4e-c^2)x^2-2cdx-d^2 = 0~$

Nous nous sommes donc ramené à la résolution d'une équation du troisième degré.

Prenons un exemple pour étudier de façon plus précise la méthode.

Soit à résoudre l'équation :

$x^4 + 4x^3 + 3x^2 - 8x - 10 = 0 ~$

Posons :

$x = z - 1 \qquad (*)~$

En remplaçant dans l'équation, on obtient :

$z^4 - 3z^2 - 6z - 2 = 0 ~$

Considérons la transformation de Tschirnhaus :

$y = z^2 + pz - \frac{3}{2} ~$

En éliminant z par des produits membre à membre successifs (voir paragraphe précédent) entre les deux relations précédentes, nous obtenons :

$y^4 - (3p^2+18p+\frac{17}{2})y^2 - (6p^3+17p^2+36p+36)y - (2p^4+9p^3+\frac{51}{4}p^2+\frac{51}{2}p+\frac{575}{16})=0 ~$

Si l'on veut que cette équation soit une équation bicarrée du quatrième degré, nous voyons que nous devons choisir p parmi les racines de l'équation :

$6x^3+17x^2+36x+36=0 ~$

Cette équation admet pour racine évidente :

$x=-\frac{3}{2} ~$

Nous choisirons donc :

$p=-\frac{3}{2} ~$

La transformation de Tschirnhaus envisagé est donc :

$y = z^2 - \frac{3}{2}z - \frac{3}{2} ~$

Et par élimination de z avec l'équation :

$z^4 - 3z^2 - 6z - 2 = 0 ~$

On obtient :

$8y^4+94y^2-49=0 ~$

En posant :

$X = y^2 ~$

On se ramène à l'équation du second degré :

$8X^2+94X-49=0 ~$

Qui a pour racines :

$X_1 = \frac{1}{2} ~$

$X_2 = -\frac{49}{4} ~$

D’où l'on déduit les quatre valeurs de y suivantes :

$y_1 = \frac{1}{\sqrt{2}} ~$

$y_2 = -\frac{1}{\sqrt{2}} ~$

$y_3 = \frac{7i}{2} ~$

$y_4 = -\frac{7i}{2} ~$

Ces quatre valeurs de y reportées dans la transformation de Tschirnhaus envisagée nous donnent quatre équations du second degré :

$z^2 - \frac{3}{2}z - \frac{3}{2} = \frac{1}{\sqrt{2}} ~$

$z^2 - \frac{3}{2}z - \frac{3}{2} =-\frac{1}{\sqrt{2}} ~$

$z^2 - \frac{3}{2}z - \frac{3}{2} = \frac{7i}{2} ~$

$z^2 - \frac{3}{2}z - \frac{3}{2} = -\frac{7i}{2} ~$

Qui se simplifient respectivement sous la forme :

$2z^2 - 3z - 3 - \sqrt{2} = 0 ~$

$2z^2 - 3z - 3 + \sqrt{2} = 0 ~$

$2z^2 - 3z - 3 - 7i = 0 ~$

$2z^2 - 3z - 3 + 7i = 0 ~$

Ces quatre équations ont respectivement comme discriminent :

$\triangle_1 = 33 + 8\sqrt{2} = (1+4\sqrt{2})^2 ~$

$\triangle_2 = 33 - 8\sqrt{2} = (1-4\sqrt{2})^2 ~$

$\triangle_3 = 33 + 56i = (7+4i)^2 ~$

$\triangle_4 = 33 - 56i = (7-4i)^2 ~$

Chacune des quatre équations du second degré fournissant deux racines, on en déduit huit valeurs possibles pour z :

$1+\sqrt{2},\frac{1}{2}-\sqrt{2},1-\sqrt{2},\frac{1}{2}+\sqrt{2},\frac{5}{2}+i,-1-i,\frac{5}{2}-i,-1+i ~$

Seules les quatre valeurs :

$z_1 = 1+\sqrt{2} ~$

$z_2 = 1-\sqrt{2} ~$

$z_3 = -1-i ~$

$z_4 = -1+i ~$

Vérifie l'équation :

$z^4 - 3z^2 - 6z - 2 = 0 ~$

Les autres valeurs sont des racines parasites apparues lors des produits membre à membre effectués pour éliminer z plus haut.

En portant les quatre valeurs valides de z dans (*), on obtient :

$x_1 = \sqrt{2} ~$

$x_2 = -\sqrt{2} ~$

$x_3 = -2-i ~$

$x_4 = -2+i ~$

Qui sont les quatre racines de l'équation que l'on s'était donné de résoudre.

Equation du cinquième degré

Voir à ce propos l'article Radical de Bring.

Remarque historique

Cette méthode est la première méthode générale de résolution des équations à avoir été publiée. Sa publication remonte à 1683.

Autres méthodes de résolution d'équations

Méthodes de résolution d'équations
Résolution d'équations polynomiales	Méthode de Bézout · Méthode de Cardan · Méthode de Sotta · Méthode de Ferrari · Méthode de Descartes · Méthode de Tschirnhaus · Méthode d'Hermite
Recherche d'un zéro	Méthode de dichotomie · Méthode de Newton · Méthode de la sécante · Méthode de Müller · Méthode de Brent · Méthode de la fausse position · Méthode de Héron · Méthode de Laguerre · Méthode du cercle de séparation · Méthode de Halley · Méthode de Householder . Méthode de Quasi-Newton

Portail des mathématiques

Ce document provient de « M%C3%A9thode de Tschirnhaus ».

Catégorie : Équation polynomiale

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Methode de Tschirnhaus de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

Méthode De Tschirnhaus — La méthode de Tschirnhaus, imaginée et mise au point par Ehrenfried Walther von Tschirnhaus, est une tentative de résoudre le point clé de la théorie des équations à savoir trouver une méthode générale de résolution de l équation polynomiale.… … Wikipédia en Français
Méthode de tschirnhaus — La méthode de Tschirnhaus, imaginée et mise au point par Ehrenfried Walther von Tschirnhaus, est une tentative de résoudre le point clé de la théorie des équations à savoir trouver une méthode générale de résolution de l équation polynomiale.… … Wikipédia en Français
Méthode de Tschirnhaus — La méthode de Tschirnhaus, imaginée et mise au point par Ehrenfried Walther von Tschirnhaus, est une tentative de résoudre le point clé de la théorie des équations à savoir trouver une méthode générale de résolution de l équation polynomiale.… … Wikipédia en Français
Methode de Sotta — Méthode de Sotta La méthode de Sotta, imaginée et mise au point par Bernard Sotta, permet de résoudre toutes les équations du troisième degré et peut se généraliser à certaines équations de degré supérieur ou égal à 4 si les coefficients de ces… … Wikipédia en Français
Méthode De Sotta — La méthode de Sotta, imaginée et mise au point par Bernard Sotta, permet de résoudre toutes les équations du troisième degré et peut se généraliser à certaines équations de degré supérieur ou égal à 4 si les coefficients de ces équations… … Wikipédia en Français
Méthode de sotta — La méthode de Sotta, imaginée et mise au point par Bernard Sotta, permet de résoudre toutes les équations du troisième degré et peut se généraliser à certaines équations de degré supérieur ou égal à 4 si les coefficients de ces équations… … Wikipédia en Français
Methode de Cardan — Méthode de Cardan La méthode de Cardan, proposée par Jérôme Cardan dans son ouvrage Ars Magna publié en 1545, est une méthode permettant de résoudre toutes les équations du troisième degré. Cette méthode permet de mettre en place des formules… … Wikipédia en Français
Méthode De Cardan — La méthode de Cardan, proposée par Jérôme Cardan dans son ouvrage Ars Magna publié en 1545, est une méthode permettant de résoudre toutes les équations du troisième degré. Cette méthode permet de mettre en place des formules appelées formules de… … Wikipédia en Français
Méthode de cardan — La méthode de Cardan, proposée par Jérôme Cardan dans son ouvrage Ars Magna publié en 1545, est une méthode permettant de résoudre toutes les équations du troisième degré. Cette méthode permet de mettre en place des formules appelées formules de… … Wikipédia en Français
Methode d'Hermite — Méthode d Hermite La méthode d’Hermite, due au mathématicien Charles Hermite, permet de résoudre les équations de degré 5 en utilisant les fonctions elliptiques. La théorie de Galois montre que les équations ne sont pas résolubles par radicaux à… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Methode de Tschirnhaus

Méthode de Tschirnhaus

Sommaire

Principe de la méthode

Application à la résolution des équations cubiques

Méthode particulière pour les équations du quatrième degré

Equation du cinquième degré

Remarque historique

Autres méthodes de résolution d'équations

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Methode de Tschirnhaus

Méthode de Tschirnhaus

Sommaire

Principe de la méthode

Application à la résolution des équations cubiques

Méthode particulière pour les équations du quatrième degré

Equation du cinquième degré

Remarque historique

Autres méthodes de résolution d'équations

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link