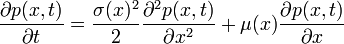- Theorie des probabilites
-
Théorie des probabilités
La Théorie des probabilités est l'étude mathématique des phénomènes caractérisés par le hasard et l'incertitude. Les objets centraux de la théorie des probabilités sont les variables aléatoires, les processus stochastiques, et les événements: ils traduisent de manière abstraite des événements non déterministes ou des quantités mesurées qui peuvent parfois évoluer dans le temps d'une manière apparemment aléatoire. En tant que fondement mathématique des statistiques, la théorie des probabilités est essentielle à la plupart des activités humaines qui nécessitent une analyse quantitative d'un grand nombre de mesures. Les méthodes de la théorie des probabilités s'appliquent également à la description de systèmes complexes dont on ne connait qu'en partie l'état, comme en mécanique statistique. Une grande découverte de la physique du vingtième siècle fut la nature probabiliste de phénomènes physiques à une échelle microscopique, décrite par la mécanique quantique.
Sommaire
Historique
La théorie mathématique des probabilités trouve ses origines dans l'analyse de jeux de hasard par Gerolamo Cardano au seizième siècle, et par Pierre de Fermat et Blaise Pascal au dix-septième siècle. Bien qu'un simple pile ou face ou un lancer de dès soit un événement aléatoire, en les répétant de nombreuses fois on obtient une série de résultats qui va posséder certaines propriétés statistiques, que l'on peut étudier et prévoir. Deux résultats mathématiques fondamentaux à ce propos sont la loi des grands nombres et le théorème de la limite centrale.
Initialement, la théorie des probabilités considérait surtout les événements discrets, et ses méthodes étaient principalement combinatoires. Mais des considérations analytiques ont forcé l'introduction de variables aléatoires continues dans la théorie. Cette idée prend tout son essor dans la théorie moderne des probabilités, dont les fondations ont été posées par Andreï Nikolaevich Kolmogorov. Kolmogorov combina la notion d'univers, introduite par Richard von Mises et la théorie de la mesure pour présenter son système d'axiomes pour la théorie des probabilités en 1933. Très vite, son approche devint la base incontestée des probabilités modernes.
Théorie des probabilités discrète
La théorie discrète des probabilités s'occupe d'événements dans le cadre d'un univers fini ou dénombrable.
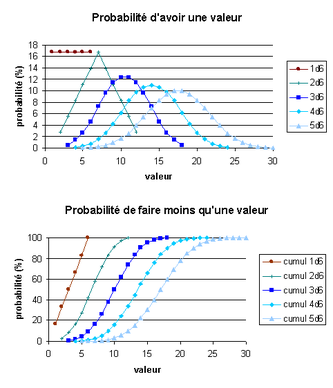
Exemples: lancer de dés, expériences avec des paquets de cartes, et marche aléatoire.
Définition classique: Initialement, la probabilité d'un événement était définie comme le nombre de cas favorables pour l'événement, divisé par le nombre total d'issues possibles à l'expérience aléatoire.
Par exemple, si l'événement est obtenir un nombre pair en lançant le dé, sa probabilité est donnée par
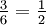 , puisque trois faces sur six ont un nombre pair.
, puisque trois faces sur six ont un nombre pair.Définition moderne : La définition moderne commence par un ensemble appelé univers, qui correspond à l'ensemble des issues possibles à l'expérience dans la définition classique. Il est noté
 . Ensuite, on a besoin d'une fonction f définie sur Ω, qui va associer à chaque élément de Ω sa probabilité, satisfaisant donc les propriétés suivantes :
. Ensuite, on a besoin d'une fonction f définie sur Ω, qui va associer à chaque élément de Ω sa probabilité, satisfaisant donc les propriétés suivantes :On définit ensuite un événement comme un ensemble d'issues, c'est-à-dire un sous-ensemble de Ω. La probabilité d'un évènement E est alors définie de manière naturelle par :
Ainsi, la probabilité de l'univers est 1, et la probabilité de l'événement impossible (l'ensemble vide) est 0.
Pour revenir à l'exemple du lancer de dés, on peut modéliser cette expérience en se donnant un univers Ω = {1;2;3;4;5;6} correspondant aux valeurs possibles du dé, et une fonction f qui à chaque
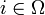 associe
associe 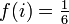 .
.Théorie des probabilités continue
La théorie des probabilités continue s'occupe des événements qui se produisent dans un univers continu (par exemple la droite réelle).
Définition classique: La définition classique est mise en échec lorsqu'elle est confrontée au cas continu (cf. paradoxe de Bertrand).
Définition moderne Si l'univers est la droite réelle
 , alors on admet l'existence d'une fonction appelée fonction de répartition
, alors on admet l'existence d'une fonction appelée fonction de répartition  , qui donne
, qui donne 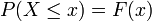 pour une variable aléatoire X. Autrement dit, F(x) retourne la probabilité que X soit inférieur ou égal à x.
pour une variable aléatoire X. Autrement dit, F(x) retourne la probabilité que X soit inférieur ou égal à x.La fonction de répartition doit satisfaire les propriétés suivantes :
 est une fonction croissante et continue à droite.
est une fonction croissante et continue à droite.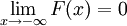
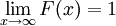
Si
 est dérivable, alors on dit que la variable aléatoire X a une densité de probabilité
est dérivable, alors on dit que la variable aléatoire X a une densité de probabilité 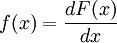 .
.Pour un ensemble
 , la probabilité que la variable aléatoire X soit dans
, la probabilité que la variable aléatoire X soit dans 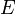 est définie comme :
est définie comme :Si la densité de probabilité existe, on peut alors la réécrire :
Tandis que la densité de probabilité n'existe que pour les variables aléatoires continues, la fonction de répartition existe pour toute variable aléatoire (y compris les variables discrètes) à valeurs dans
 .
.Ces concepts peuvent être généralisés dans les cas multidimensionnel sur
 et d'autres univers continus.
et d'autres univers continus.Principes fondamentaux
La probabilité d'un événement donné A,
 , est représentée par un nombre compris entre 0 et 1. L'événement impossible a une probabilité de 0 et l'événement certain a une probabilité de 1. Il faut savoir que la réciproque n'est pas vraie. Un événement qui a une probabilité 0 peut très bien se produire dans le cas où un nombre infini d'événements différents peut se produire. Ceci est détaillé dans l'article Ensemble négligeable.
, est représentée par un nombre compris entre 0 et 1. L'événement impossible a une probabilité de 0 et l'événement certain a une probabilité de 1. Il faut savoir que la réciproque n'est pas vraie. Un événement qui a une probabilité 0 peut très bien se produire dans le cas où un nombre infini d'événements différents peut se produire. Ceci est détaillé dans l'article Ensemble négligeable.Quelques notions ou propriétés fondamentales Évènement Probabilité probabilité de A ![\mathbb{P}(A)\in[0,1]\,](/pictures/frwiki/101/e80064214aea988389b07fc8d173b9cd.png)
probabilité de ne pas avoir A 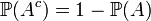
probabilité d'avoir A ou B 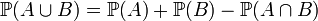
probabilité conditionnelle de A,
sachant B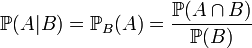
probabilité d'avoir A et B 
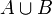 est la réunion de A et B.
est la réunion de A et B. 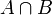 est l'intersection de A et de B.
est l'intersection de A et de B. 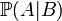 est appelé la probabilité conditionnelle de A sachant B. C'est la probabilité d'avoir A quand on sait que l'on a B. Par exemple, pour un dé à 6 faces la probabilité d'avoir un 2 (A) quand on sait que le résultat est pair (B) est égal à
est appelé la probabilité conditionnelle de A sachant B. C'est la probabilité d'avoir A quand on sait que l'on a B. Par exemple, pour un dé à 6 faces la probabilité d'avoir un 2 (A) quand on sait que le résultat est pair (B) est égal à 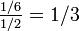 car la probabilité d'avoir à la fois un 2 et un nombre pair est égal à 1/6 et la probabilité d'avoir un nombre pair est égal à 1/2. Ici on remarque que
car la probabilité d'avoir à la fois un 2 et un nombre pair est égal à 1/6 et la probabilité d'avoir un nombre pair est égal à 1/2. Ici on remarque que 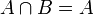 car on a toujours un nombre pair quand on a 2.
car on a toujours un nombre pair quand on a 2.La théorie des probabilités aujourd'hui
Article détaillé : axiomes des probabilités.Article détaillé : espace probabilisé.Certaines distributions peuvent être un mélange de distributions discrètes et continues, et donc n'avoir ni densité de probabilité ni fonction de masse. La distribution de Cantor constitue un tel exemple. L'approche moderne des probabilités résout ces problèmes par l'utilisation de la théorie de la mesure pour définir un espace probabilisé et aboutir aux axiomes des probabilités développés par Kolmogorov
Un espace probabilisé comporte trois parties:
- un univers Ω: L'univers est l'ensemble de tous les résultats possibles de l'évenement aléatoire. Par exemple pour un dé a 6 faces l'univers est Ω ≡ {1, 2, 3, 4, 5, 6}.
- un ensemble d'événements
 : C'est une tribu sur les événements Ω. Cet ensemble contient tous les résultats possibles de l'événement au sens large. Par exemple pour un dé à 6 faces il contient la possibilité d'avoir un 1 ou un 2: {1, 2}, la possibilité de ne rien sortir comme résultat: l'ensemble vide
: C'est une tribu sur les événements Ω. Cet ensemble contient tous les résultats possibles de l'événement au sens large. Par exemple pour un dé à 6 faces il contient la possibilité d'avoir un 1 ou un 2: {1, 2}, la possibilité de ne rien sortir comme résultat: l'ensemble vide 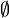 , la possibilité de sortir n'importe quel face du dé {1, 2, 3, 4, 5, 6}. En général en probabilité on se contente de prendre la tribu borélienne. À titre d'exemple la tribu borélienne pour le résultat d'un dé à 4 faces est donné (celle pour le dé à 6 faces est encore plus grande mais suit le même principe):
, la possibilité de sortir n'importe quel face du dé {1, 2, 3, 4, 5, 6}. En général en probabilité on se contente de prendre la tribu borélienne. À titre d'exemple la tribu borélienne pour le résultat d'un dé à 4 faces est donné (celle pour le dé à 6 faces est encore plus grande mais suit le même principe):
- {ø, {1}, {2}, {3}, {4}, {1,2}, {1,3}, {1,4}, {2,3}, {2,4}, {3,4}, {1,2,3}, {1,2,4}, {1,3,4}, {2,3,4}, {1,2,3,4}}. On remarque que cette tribu contient l'ensemble vide ø et Ω={1,2,3,4}. Ceci est le cas pour toutes les tribus.
- une mesure
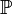 : Cette mesure ou probabilité est la probabilité de réaliser l'un des éléments de
: Cette mesure ou probabilité est la probabilité de réaliser l'un des éléments de  . Cette probabilité est comprise entre 0 et 1 pour tous les éléments de
. Cette probabilité est comprise entre 0 et 1 pour tous les éléments de  , c'est le premier axiome des probabilités. Par exemple pour un dé a 6 faces: la probabilité d'avoir {1} est 1/6, la probabilité de Ω={1, 2, 3, 4, 5, 6}, tirer n'importe laquelle des 6 faces, est 1 (ceci est aussi toujours le cas, c'est le deuxième axiome des probabilités), la probabilité de l'ensemble vide ø est 0. Ceci est toujours le cas, c'est également une conséquence des axiomes des probabilités.
, c'est le premier axiome des probabilités. Par exemple pour un dé a 6 faces: la probabilité d'avoir {1} est 1/6, la probabilité de Ω={1, 2, 3, 4, 5, 6}, tirer n'importe laquelle des 6 faces, est 1 (ceci est aussi toujours le cas, c'est le deuxième axiome des probabilités), la probabilité de l'ensemble vide ø est 0. Ceci est toujours le cas, c'est également une conséquence des axiomes des probabilités.
Dans cette optique, pour des événements deux à deux disjoints (c'est-à-dire, d'intersection deux à deux vide) A1, A2, A3…, la probabilité de leur union apparaît comme la somme de leurs probabilités, ou, avec les notations mathématiques,
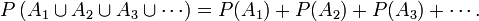
C'est le troisième et dernier axiome des probabilités. Par exemple, et toujours pour un dé à 6 faces, la probabilité de tirer un 1 ou un 2

En plus de permettre une meilleure compréhension et une unification des théories discrètes et continues des probabilités, l'approche de la théorie de la mesure nous permet aussi de parler de probabilités en dehors de
 , notamment dans la théorie des processus stochastiques. Par exemple pour l'étude du mouvement brownien, la probabilité est définie sur un espace de fonctions.
, notamment dans la théorie des processus stochastiques. Par exemple pour l'étude du mouvement brownien, la probabilité est définie sur un espace de fonctions.Lois de probabilité
Article détaillé : Loi de probabilité.Certaines variables aléatoires sont fréquemment rencontrées en théorie des probabilités car on les retrouve dans de nombreux processus naturels ; leur loi a donc une importance particulière. Les lois discrètes les plus fréquentes sont la loi uniforme discrète, la loi de Bernoulli, ainsi que les lois binomiale, de Poisson et géométrique. Les lois uniforme continue, normale, exponentielle et gamma sont parmi les plus importantes lois continues.
Convergence de variables aléatoires
Article détaillé : convergence de variables aléatoires.En théorie des probabilités, il y a plusieurs notions de convergence pour les variables aléatoires. En voici une liste:
- Convergence en loi: une suite de variables aléatoires
 converge en loi vers la variable aléatoire
converge en loi vers la variable aléatoire 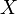 si et seulement si la suite des mesures images
si et seulement si la suite des mesures images  converge étroitement vers la mesure image μX. En particulier dans le cas réel, il faut et il suffit que les fonctions de répartition convergent simplement vers la fonction de répartition de X en tout point de continuité de cette dernière.
converge étroitement vers la mesure image μX. En particulier dans le cas réel, il faut et il suffit que les fonctions de répartition convergent simplement vers la fonction de répartition de X en tout point de continuité de cette dernière. - Convergence en probabilité:
 converge en probabilité vers
converge en probabilité vers 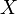 ssi
ssi 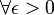 ,
, 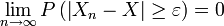 . Cette convergence implique la convergence en loi.
. Cette convergence implique la convergence en loi. - Convergence presque sûre:
 converge presque sûrement vers
converge presque sûrement vers 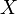 ssi
ssi 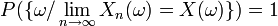 . Elle implique la convergence en probabilité, donc la convergence en loi.
. Elle implique la convergence en probabilité, donc la convergence en loi. - Convergence dans
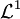 :
:  converge dans
converge dans 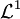 vers
vers 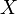 ssi
ssi 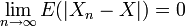 . Elle implique aussi la convergence en probabilité.
. Elle implique aussi la convergence en probabilité.
Le calcul stochastique
Article détaillé : calcul stochastique.Un processus stochastique est un processus aléatoire qui dépend du temps. Un processus stochastique est donc une fonction de deux variables : le temps et la réalisation ω d'une certaine expérience aléatoire. Quelques exemples d'utilisation des processus stochastiques incluent le mouvement brownien, les fluctuations du marché boursier, ou la reconnaissance vocale. En temps discret, ces processus sont aussi connus sous le nom de Séries temporelles et servent entre autres en économétrie.
Parmi les processus stochastiques, les chaînes de Markov constituent l'exemple le plus simple et sans doute celui qui a le plus d'applications pratiques.
Chaîne de Markov
Article détaillé : chaîne de Markov.Une chaîne de Markov est un processus stochastique possédant la propriété markovienne. Dans un tel processus, la prédiction du futur à partir du présent ne nécessite pas la connaissance du passé. Il suffit alors de connaître l'état de la chaîne à un instant t pour savoir comme elle évoluera au temps t+1, il n'est pas nécessaire de connaître tout le passé entre 0 et t pour prévoir l'évolution de la chaîne.
Une chaîne en temps discret est une séquence X1, X2, X3, ... de variables aléatoires. La valeur Xn étant l'état du processus au moment n. Si la distribution de probabilité conditionnelle de Xn+1 sur les états passés est une fonction de Xn seulement, alors de façon mathématique:
où x est un état quelconque du processus,
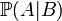 est la probabilité d'avoir A quand on sait que l'on a B par exemple ici la probabilité d'avoir une certaine valeur pour Xn + 1 quand on connaît la valeur de Xn. L'identité ci-dessus est la propriété de Markov pour le cas particulier d'une chaîne en temps discret. La probabilité P(Xn + 1 = x | Xn = y) est appelée la probabilité de transition de x à y ; c'est la probabilité d'aller de x à y au temps n et a une importance particulière pour l'étude de ces chaînes. Nous considérons ici uniquement des chaînes de Markov en temps discret mais il faut savoir qu'il existe une généralisation en temps continu.
est la probabilité d'avoir A quand on sait que l'on a B par exemple ici la probabilité d'avoir une certaine valeur pour Xn + 1 quand on connaît la valeur de Xn. L'identité ci-dessus est la propriété de Markov pour le cas particulier d'une chaîne en temps discret. La probabilité P(Xn + 1 = x | Xn = y) est appelée la probabilité de transition de x à y ; c'est la probabilité d'aller de x à y au temps n et a une importance particulière pour l'étude de ces chaînes. Nous considérons ici uniquement des chaînes de Markov en temps discret mais il faut savoir qu'il existe une généralisation en temps continu.Cette propriété de Markov s'oppose à la notion d'hystérésis où l'état actuel dépend de l'histoire et non seulement de l'état actuel. Ces chaînes de Markov ou des modèles de Markov cachés interviennent dans l'étude de la marche aléatoire et ont de nombreux champs d'application: filtre anti-spam, mouvement brownien, hypothèse ergodique, théorie de l'information, reconnaissance des formes, algorithme de Viterbi utilisé en téléphonie mobile, etc...
Article détaillé : marche aléatoire.Citons entre autres comme cas particuliers de chaînes de Markov la marche aléatoire qui sert en particulier à l'étude de la diffusion ou du jeu de pile ou face. Une marche aléatoire est une chaîne de Markov où la probabilité de transition ne dépend que de x-y. Autrement dit une chaîne de Markov où l'on a: P(Xn + 1 = x | Xn = y) = f(x − y).
Un jeu de pile ou face où l'on jouerait 1 à chaque lancer est un exemple de marche aléatoire. Si on a y après n lancers, P(Xn + 1 = x | Xn = y) = 1 / 2 si (x-y)=+1 ou -1 et 0 sinon. (on a une chance sur deux de gagner 1 et une chance sur deux de perdre 1)
Équations différentielles stochastiques
Article détaillé : Équation différentielle stochastique.Les équations différentielles stochastiques sont une forme d'équation différentielle incluant un terme de bruit blanc. Ces équations différentielles stochastiques remplacent les équations différentielles ordinaires lorsque l'aléatoire entre en jeu. Au premier ordre par exemple:
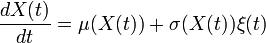
Pour faire une analogie avec la physique, μ(X(t)) est la vitesse moyenne au point X(t) et σ est lié au coefficient de diffusion (voir à ce propos l'exemple donné dans lemme d'Itô). Le lemme d'Itô et l'intégrale d'Itô permettent alors de passer de ces équations stochastiques à des équations aux dérivées partielles classiques ou à des équations intégrales. Par exemple en utilisant le lemme d'Itô on obtient pour la probabilité de se trouver à l'instant t au point x:
Ce lemme est particulièrement important car il permet de faire le lien entre l'étude d'équations stochastiques et les équations aux dérivées partielles qui relèvent de l'analyse. Ce lemme permet entre autres d'obtenir les équation de Fokker-Planck en physique et de traiter le mouvement brownien par des équations aux dérivées partielles classiques ou de modéliser les cours de la bourse en Mathématiques financières.
Voir aussi
Articles connexes
Liens externes
- Jean-François Le Gall, Intégration, probabilités et processus aléatoires [pdf], cours de l'ENS.
- Portail des probabilités et des statistiques
Catégories : Probabilités | Théorie
Wikimedia Foundation. 2010.

![f(x)\in[0,1]\mbox{ pour tout }x\in \Omega](/pictures/frwiki/48/0e77ec055bf042c11b977174cb518c4d.png)
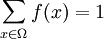
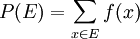
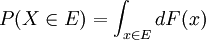
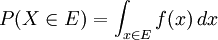
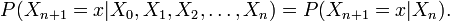
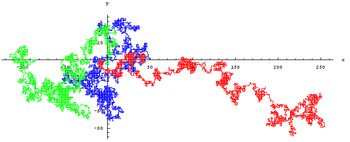
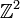 ; 10 000 pas.
; 10 000 pas.