Anneau Factoriel

Anneau factoriel

En mathématiques, un anneau factoriel est un cas particulier d'anneau commutatif, unitaire et intègre. À l'image des nombres entiers, il existe un équivalent du théorème fondamental de l'arithmétique pour une telle structure. Tout élément d'un anneau factoriel se décompose en un produit d'un élément inversible et d'éléments irréductibles. Un élément irréductible est un élément qui, dans une décomposition en produit de deux facteurs, contient toujours un élément inversible. Par exemple dans Z, l'anneau des entiers, -2 est irréductible. La décomposition en facteurs irréductibles est unique dans un anneau factoriel, aux éléments inversibles près.

Les exemples d' anneau factoriel ne sont pas rares. Tout anneau principal, c'est-à-dire tel que tout idéal est principal est factoriel. La réciproque n'est pas vraie. Ainsi un anneau de polynômes à coefficients dans un anneau factoriel est factoriel mais n'est pas principal si l'anneau n'est pas un corps. En ce sens, le concept d'anneau factoriel généralise celui d'anneau principal.

Certains résultats usuels de l'arithmétique élémentaire s'appliquent sur un anneau factoriel. Ainsi, le lemme d'Euclide est vérifié et il est possible de définir un plus grand commun diviseur et un plus petit commun multiple bénéficiant presque des propriétés usuelles sur Z.

Définitions

Une première définition est nécessaire pour exprimer celle d'anneau factoriel :

Un élément a non nul d'un anneau commutatif unitaire et intègre est dit irréductible si et seulement s'il n'est pas inversible et si toute décomposition en deux facteurs b et c de a, a = b.c comporte un élément inversible (soit b soit c).

La définition la plus courante d'anneau factoriel est :

Un anneau commutatif unitaire intègre A est dit factoriel si et seulement s'il vérifie les deux propriétés suivantes :

(1) Pour tout élément a non nul de A, il existe un élément inversible u et une suite finie p₁, …, p_n d'éléments irréductibles de A tel que :

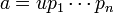
$a = u p_1\cdots p_n\;$

(2) La decomposition est unique au sens suivant. Soit v un élément inversible et q₁ … q_m une deuxième décomposition de a :

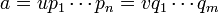
$a = u p_1\cdots p_n= v q_1\cdots q_m \;$

alors n est égal à m et il existe une permutation $σ$ de l'ensemble [1, n] et des éléments inversibles w_i tel que :

$\forall i \in [1,n ]\quad p_i = w_iq_{\sigma (i)}\;$ ^[1]

Dans un anneau factoriel A, il est possible de définir une relation d'association entre éléments irréductibles. Deux éléments irréductible p et q de A sont associés s'il existe un élément inversible u tel que p = u.q. Cette relation est une relation d'équivalence. Certains anneaux possèdent des éléments irréductibles particuliers, ainsi un élément irréductible et positif de Z est appelé nombre premiers. Dans K[X] les éléments particuliers sont les polynômes irréductibles unitaires, c'est-à-dire dont le coefficient du monôme dominant est égal à un. Chaque classe d'équivalence contient un unique élément irréductible particulier. Cette approche permet de normaliser la décomposition en facteurs irréductibles de telle sorte que l'unicité ne soit plus définie aux éléments inversibles près.

Il est toujours possible d'établir une normalisation de cette nature. Il suffit de définir une famille (p_i) d'éléments irréductibles tel que si i est différent de j alors p_i n'est pas associé à p_j et si π est un élément irréductible il existe un indice i tel que π est associé à p_i. Le lemme de Zorn montre qu'il est toujours possible de trouver une famille maximale d'éléments irréductibles deux à deux non associés. Cette normalisation est utilisée dans la suite de l'article pour ne pas alourdir les énoncées. Elle n'est pas nécessaire, cependant les unicités s'expriment alors aux éléments inversibles près. Un élément a d'un anneau factoriel s'écrit :

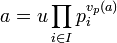
$a =u \prod_{i\in I}p_i^{v_p(a)}$

La fonction de A dans N, l'ensemble des entiers naturels, qui à a associe v_{p_i}(a) s'appelle une valuation p-adique. La valeur v_{p_i}(a) est aussi appelée ordre de multiplicité de p_i dans a.

Dans la suite de l'article A désigne un anneau factoriel et (p_i) une telle famille d'éléments irréductibles (sauf mention explicite contraire).

Motivation

L'arithmétique dans l'anneau des entiers relatifs permet la démonstration de nombreux théorèmes. Les démonstrations utilisent le fait que cet anneau est euclidien donc principal. En revanche, de nombreux anneaux ne le sont pas, par exemple celui des polynômes à coefficients dans les entiers relatifs ou encore les polynômes en plusieurs indéterminées sur un corps commutatif.

Ce dernier exemple est important, les variétés algébriques sont définies comme les racines d'un idéal de polynômes à plusieurs variables. Ainsi la sphère réelle est définie comme les racines communes des polynômes à trois indéterminées multiples de X² + Y² + Z² - 1. L'anneau des fonctions polynomiales définies sur la sphère n'est ni euclidien ni principal. En revanche, il est factoriel.

Sur un anneau factoriel, certains théorèmes fondamentaux des anneaux principaux restent vrais. Ainsi, le lemme d'Euclide, les propriétés des plus petits communs multiples et des plus grands communs diviseur ou encore le théorème fondamental de l'arithmétique restent valables (ce dernier est vérifié par définition).

Tous ne s'appliquent plus, ainsi un idéal premier n'est pas toujours maximal. Dans Z[X], l'anneau des polynômes à coefficients dans Z, l'anneau des entiers relatifs, 2Z[X] n'est pas maximal et Z[X] / 2Z[X] n'est pas un corps car la classe de X n'est pas inversible. L'identité de Bézout n'est pas toujours vérifiée, dans Z[X] les éléments 2 et X n'ont pas de facteur commun, pourtant l'idéal engendré par 2 et X n'est pas l'anneau tout entier.

Exemples et contre-exemples

L'anneau Z est évidemment le premier exemple d'anneau factoriel. Mais on trouve aussi l'anneau de Gauss Z[i] des complexes s'écrivant sous la forme a + ib où a et b sont des entiers relatifs.
Si K est un corps alors l'ensemble K[X] des polynômes à coefficient dans K est un anneau factoriel, ainsi que K[X₁, X₂, ...,X_n]. Plus généralement, dès que A est factoriel, il en est de même de A[X].
On démontre que tout anneau euclidien ou tout anneau principal est aussi factoriel
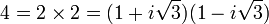Le contre-exemple le plus célèbre est l'anneau non-factoriel $\mathbb Z[i\sqrt 3]$ dans lequel on trouve deux décompositions différentes de 4 : $4 = 2 \times 2 = (1 + i\sqrt{3})(1 - i\sqrt{3})$ . Propriété qui donna l'occasion à Leonhard Euler de présenter une démonstration fausse du dernier théorème de Fermat pour n = 3 (Algebra 1770). Pour pallier cette difficulté, la méthode la plus simple est d'utiliser les entiers d'Eisenstein. La configuration générale d'une situation de cette nature est étudiée dans l'article sur l'entier quadratique. Pour trouver une solution très générale à cette difficulté Ernst Kummer crée des nombres idéaux, maintenant formalisé par les travaux de Richard Dedekind à travers le concept d'anneau de Dedekind.
Un contre-exemple "géométrique" est celui du quotient de K[X,Y,Z] par l'idéal engendré par $X 2 - Y Z$ .

Soit p l'application de passage au quotient. $p (X 2)$ admet deux décompositions distinctes en facteurs irréductibles : on a $p (X 2) = p (X) p (X)$ mais aussi $p (X 2) = p (Y) p (Z)$

Propriétés

Premières propriétés

Un anneau commutatif unitaire et intègre est factoriel si et seulement s'il vérifie les deux propriétés suivantes :

(1) Toute suite d'idéaux principaux croissantes est stationnaire à partir d'un certain rang.

(2) Tout idéal engendré par un élément irréductible est premier.^[2]

Cette caractéristique est parfois plus simple pour établir le caractère factoriel d'un anneau. La proposition suivante en est un exemple :

Tout anneau principal est factoriel.

En effet, un anneau principal est noethérien, la première propriété est ainsi vérifiée. De plus si p est irréductible, l'idéal des multiples de p est premier et maximal. Ces propriétés sont démontrées dans l'article Anneau principal.

Tout anneau factoriel est intégralement clos.

Comme un anneau factoriel A est commutatif unitaire intègre, il est possible de considérer son corps des fractions. Un élément de K est dit entier sur A si son polynôme minimal est à coefficients dans A. L'article Polynôme minimal d'un nombre algébrique montre que l'ensemble B des entiers algébriques de K sur A forme un anneau. Si B est égal à A, alors A est dit intégralement clos. La démonstration est identique à celle présentée dans l'article Anneau principal.

Soit π est un élément irréductible de A, si π divise le produit de deux éléments a et b, alors il divise soit a soit b.

Ce résultat est connu sous le nom de lemme d'Euclide ou parfois lemme de Gauss. Il est la conséquence directe de l'unicité de la décomposition de a.b en facteurs irréductibles.

Démonstration

Un anneau commutatif unitaire et intègre est factoriel s'il vérifie les deux propriétés suivantes :

(1) Toute suite d'idéaux principaux croissantes est stationnaire à partir d'un certain rang.

(2) Tout idéal engendré par un élément irréductible est premier.

En vue de montrer cette implication, une décomposition de la démonstration est utile. Soient A un anneau vérifiant les hypothèses de la première définition et a un élément de A non nul.

Il existe un élément irréductible qui divise a si a n'est pas inversible :

Si a est irréductible la proposition est démontrée, sinon on construit par récurrence une suite (a_n) par récurrence de la manière suivante, a₀ est égal à a, supposons la suite définie jusqu'à l'ordre n – 1, si a_{n - 1} est irréductible alors a_n est égal à a_{n - 1}, sinon a_n est un diviseur strict de a_{n - 1}. L'élément b de A est dit diviseur strict de a_{n - 1} s'il n'est pas inversible et s'il existe un élément c de A non inversible tel que b.c soit égal à a_{n - 1}.

La suite des idéaux principaux (a_nA) est croissante, la première partie de la définition indique qu'elle est stationnaire à partir d'un certain rang, noté ici m. Le fait que la suite soit stationnaire montre que a_m est irréductible. Par construction, il divise a.

Il existe un élément inversible u est une suite finie p₁, …, p_n d'éléments irréductibles de l'anneau tel que :

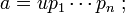
$a = u p_1\cdots p_n\ ;$

Si a est irréductible ou inversible, la proposition est évidente. Sinon le résultat précédent montre l'existence d'un élément irréductible p₁ et d'un élément u₁ tel que a = p₁.u₁. Si u₁ est inversible alors la proposition est démontrée, sinon il existe un élément p₂ irréductible et un élément u₂ tel que a = p₁.p₂.u₁. En réitérant le raisonnement on trouve soit un élément u_n inversible et la proposition est démontrée soit une suite infinie (u_i). La suite des idéaux (u_iA) est alors strictement croissante, ce qui est impossible. Cette impossibilité démontre la proposition.

La décomposition en facteurs irréductibles est unique :

On suppose l'existence de deux décompositions :

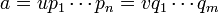
$a = u p_1\cdots p_n= v q_1\cdots q_m \;$

Montrons la proposition par récurrence sur n. Si n est égal à zéro, alors a est inversible, m est aussi égal à zéro et la proposition est démontrée.

Supposons la proposition démontrée à l'ordre n – 1, et montrons la à l'ordre n. L'élément p_n divise le produit vq₁ …q_m, on en déduit que l'idéal premier p_nA contient vq₁ …q_m. Comme l'idéal est premier et que v est inversible, il existe un élément k tel que q^k est élément de l'idéal et q _k est un multiple de p_n. Comme l'élément q _k est irréductible, il existe un élément inversible w_n tel que p_n = w_n.q _k.

L'égalité suivante et l'hypothèse de récurrence permettent de conclure :

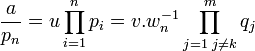
$\frac a{p_n} = u\prod_{i=1}^n p_i = v.w_n^{-1}\prod_{j=1\; j\neq k}^m q_j$

Si l'anneau est factoriel, il vérifie les propriétés (1) et (2) :

Soit σ la fonction de A – {0} dans N l'ensemble des entiers naturels qui à a associe le nombre de facteurs non inversibles dans la décomposition en facteurs irréductibles de a. L'unicité de la décomposition dans un anneau factoriel montre que la fonction σ est bien définie.

Soit a et b deux éléments non nuls de A. L'unicité de la décomposition montre aussi que σ(a.b) = σ(a) + σ(b). Ainsi si c divise strictement a, alors σ(a) est strictement plus grand que σ(c).

Toute suite d'idéaux principaux croissante est stationnaire :

Soit (a_nA) une suite d'idéaux principaux croissante. Si la suite des (a_n) est constante égal à zéro, la suite est stationnaire. Sinon, quitte à réindexer la suite, supposons que a₁ ne soit pas nul. Dire que l'idéal a_{n + 1}A contient strictement l'idéal a_nA signifie que a_{n + 1} divise strictement a_nA. On en déduit que la suite (a_nA) n'est strictement croissante qu'un nombre de fois inférieur ou égal à σ( a₁) ce qui montre que la suite est stationnaire au bout d'un certain rang.

Soit p un élément irréductible de A, l'idéal pA est premier :

Soit a et b deux éléments de A tel que ab est élément de pA. Alors ab est un multiple de p, la décomposition en facteurs irréductibles de ab contient nécessairement p à un facteur inversible près. En conséquence soit la décomposition de a soit celle de b contient p, à un facteur inversible près. Ce qui montre que soit a soit b est élément de l'idéal pA. Cette propriété traduit le fait que l'idéal est premier et termine la démonstration.

Diviseur et multiple communs

Soit (a_n) une suite d'éléments de A, le plus grand commun diviseur de la suite est le produit de tous les facteurs p_i présents dans la décomposition en facteur irréductible de chaque a_n avec le plus petit ordre de multiplicité trouvée dans la décomposition des a_n.

Le plus petit commun multiple de la famille (a_n), s'il existe, est le produit des facteurs p_i présent dans une au moins des décompositions en facteurs irréductibles d'un élément a_n avec le plus grand ordre de multiplicité. Si la famille des indices est finie, le plus petit commun multiple existe toujours.

Une famille d'éléments de A est dite première entre elle si et seulement si le plus grand diviseur commun à la famille est égal à un. Dans ce cas, les éléments de la famille sont dit premiers entre eux dans leur ensemble.

Ces définitions généralisent les notions de plus petit commun multiple et plus grand commun diviseur. Dans ce contexte, certaines des propriétés vraies sur un anneau principal s'appliquent encore, d'autres non. La relation d'ordre utilisée ici est celle induite par l'inclusion des idéaux. L'élément a est dit 'plus petit qu'un élément b si et seulement si l'idéal engendré par a contient l'idéal engendré par b.

Soient (a_n) une famille d'éléments de A et b un élément de a, la relation suivante est vérifiée :

$\text{pgcd} (b\cdot a_n)=b \cdot\text{pgcd} (a_n)\;$

Soient (a_n) une famille finie d'éléments de A et b un élément de a, la relation suivante est vérifiée :

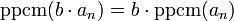
$\text{ppcm} (b\cdot a_n)=b \cdot\text{ppcm} (a_n)\;$

Soient (a_n) une famille finie d'éléments de A premiers entre eux deux à deux, la relation suivante est vérifiée :

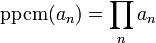
$\text{ppcm} (a_n)= \prod_n a_n\;$

Soient a et b deux éléments de A, la propriété suivante est vérifiée, si G désigne le groupe des unités:

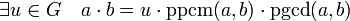
$\exists u \in G\quad a\cdot b = u\cdot \text{ppcm} (a,b)\cdot \text{pgcd} (a,b)\;$

Soit (a_n) une famille d'éléments de A, le plus petit idéal principal contenant tous les a_n est l'idéal engendré par le plus grand commun diviseur de la famille (a_n).

En effet, il suffit de remarquer que tout élément de l'idéal engendré par la famille est multiple du plus grand commun diviseur et si un élément c de A est plus grand que le plus grand commun diviseur, alors il existe un élément a_i de la famille qui n'est pas multiple de c. Le plus petit idéal principal contenant tous les a_n n'est pas nécessairement l'idéal engendré par la famille, car cet idéal n'est pas nécessairement principal. Ainsi dans Z[X] l'idéal engendré par 2 et X est l'idéal des polynômes admettant une constante multiple de deux, le plus petit idéal principal le contenant est l'idéal entier. Dans un anneau principal, les deux idéaux sont confondus. Ce résultat est connu sous le nom de théorème de Bachet-Bézout.

Soit (a_n) une famille d'éléments de A admettant un plus petit commun multiple, l'intersection des idéaux engendrés par la famille (a_n) est l'idéal principal engendré par le plus petit commun multiple.

Si A est quotienté par la relation d'équivalence R d'association définie dans le paragraphe Définitions, alors l'ensemble A/R munis des opérateurs pgcd et ppcm forme un treillis.

Anneau des polynômes

Les anneaux de polynômes représentent la première motivation historique pour les anneaux factoriels. Si les coefficients sont choisi dans un corps commutatif, l'anneau dispose d'une division euclidienne, dans le cas contraire une autre arithmétique apparaît. En 1801 Carl Friedrich Gauss (1777 - 1855) publie un traité^[3] dans lequel il montre que l'anneau des polynômes à coefficients entiers possède un propriété qui se traduit, en terme moderne, par le fait que cet anneau est factoriel. Une présentation moins générale est proposée dans l'article lemme de Gauss.

Dans ce paragraphe A désigne un anneau factoriel et K son corps des fractions. Il est nécessaire pour étudier les polynômes à coefficients dans un anneau factoriel, d'expliciter quelques définitions :

Un polynôme de A[X] est dit primitif si et seulement si les coefficients du polynôme sont premiers entre eux dans leur ensemble.

Le contenu d'un polynôme P à coefficients dans K, s'il existe, est un élément a de K tel qu'il existe un polynôme primitif Q de A[X] tel que aQ soit égal à P. Dans cet article, on note cont (P) le contenu de P.^[4]

Le contenu d'un polynôme vérifie les propriétés suivantes :

Le contenu d'un polynôme est défini à un facteur inversible de A près.

Le contenu d'un polynôme P non nul à coefficients dans K est toujours défini et il existe un polynôme primitif Q, à coefficients dans A tel que :

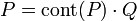
$P = \text{cont}(P)\cdot Q\;$

Soit P et Q deux polynômes non nuls à coefficients dans K, l'égalité suivante est vérifiée, à un facteur inversible près :

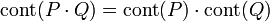$\text{cont}(P\cdot Q) = \text{cont}(P)\cdot \text{cont}(Q)\;$ ^[5]

Le résultat suivant est connu sous le nom de lemme de Gauss dans le cas où A est l'anneau Z des entiers relatifs :

Soit P un polynôme non constant à coefficients dans A. Le polynôme est irréductible dans A[X] si et seulement s'il est primitif et irréductible dans K[X].

Ce lemme permet de démontrer le théorème suivant :

L'anneau A[X] est factoriel.

On en déduit immédiatement le corollaire suivant :

Soit n un entier strictement positif, l'anneau A[X₁, ..., X_n] est factoriel.^[6]

Démonstrations

Le contenu d'un polynôme est défini à un facteur inversible de A près :

Soit P un polynôme de K[X], deux éléments de K a₁, a₂, deux éléments de K^* b₁, b₂ et deux polynômes primitifs de A[X] Q₁, Q₂ tel que :

$P[X] = \frac {a_1}{b_1}Q_1 = \frac{a_2}{b_2}Q_2\;$

On en déduit que a₁.b₂ est le pgcd des coefficients du polynôme de A[X] a₁.b₂Q₁ et a₂.b₁ est le pgcd des coefficients du polynôme de A[X] a₂.b₁Q₂. Ces deux polynômes sont égaux, ce qui montre que les pgcd diffèrent d'un facteur multiplicatif de A inversible et démontre la proposition.

Le contenu d'un polynôme P non nul à coefficients dans K est toujours défini et il existe un polynôme primitif Q, à coefficients dans A tel que :

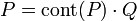
$P = \text{cont}(P)\cdot Q\;$

Notons le polynôme P de la manière suivante :

$P = \frac {a_n}{b_n}X^n + \frac {a_{n-1}}{b_{n-1}}X^{n-1} + \cdots + \frac {a_0}{b_0}$

Les familles (a_i) et (b_i) sont choisies de telle sorte que, pour tout i élément de zéro, les n couples a_i et b_i sont formés d'éléments premiers entre eux. Notons g le plus petit commun multiple de la famille (b_i). Il existe alors une famille (c_i) tel que pour tout i, g = b_i.c_i. On en déduit une nouvelle écriture du polynôme :

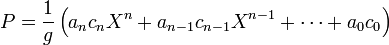
$P = \frac 1g \left(a_nc_nX^n + a_{n-1}c_{n-1}X^{n-1} + \cdots + a_0c_0\right)$

Soit h le plus grand commun diviseur de la famille (a_i.c_i). Il existe une famille (d_i) d'éléments de A premiers entre eux dans leur ensemble tel que pour tout i, a_i.c_i = d_ih et :

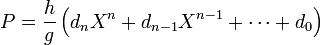
$P = \frac hg \left(d_nX^n + d_{n-1}X^{n-1} + \cdots + d_0\right)$

Ce qui montre la proposition.

Soit P et Q deux polynômes non nuls à coefficients dans K, l'égalité suivante est vérifiée, à un facteur inversible près :

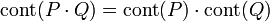
$\text{cont}(P\cdot Q) = \text{cont}(P)\cdot \text{cont}(Q)\;$

La proposition précédente montre qu'il suffit de montrer l'égalité pour deux polynômes à coefficients dans A et primitif. Pour cela raisonnons par contraposée. Montrons que si P.Qn'est pas primitif alors soit P soit Q n'est pas primitif. Si P.Q n'est pas primitif, il existe un élément irréductible p qui divise chacun des coefficients. Soit J un idéal maximal contenant p et φ le morphisme canonique de l'anneau A[X] dans A / pA[X]. Par hypothèse p divise chacun des coefficients de P.Q, on en déduit que φ(P.Q) égal à φ(P).φ(Q) est nul. Comme A / pA est un corps, soit φ(P), soit φ(Q) est nul, ce qui revient à dire que p divise le contenu de P ou de Q. La contraposée indique que si P et Q sont primitifs, alors P.Q l'est aussi.

Soit P un polynôme non constant à coefficients dans A. Le polynôme est irréductible dans A[X] si et seulement s'il est primitif et irréductible dans K[X] :

Supposons P irréductible, il est possible d'écrire ce polynôme sous forme d'un produit d'un polynôme constant égal à son contenu et d'un polynôme primitif. Ceci montre que son contenu est un polynôme inversible donc de degré zéro et égal à un élément inversible ce qui signifie que le polynôme est primitif.

Montrons qu'un polynôme P primitif et non constant à coefficients dans A est décomposable dans K[X] si et seulement s'il est décomposable dans A[X]. Si P est décomposable dans K alors il existe deux polynômes B et C de degré supérieur ou égal à un et à coefficients dans K tel que P = A.B. Une proposition précédente montre l'existence de deux polynômes primitifs Q et R tel que :

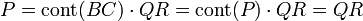
$P = \text{cont}(B C)\cdot QR = \text{cont}(P)\cdot QR=QR\;$

Réciproquement, si le polynôme est primitif et décomposable dans A[X] alors la décomposition comporte deux facteurs de degré supérieur ou égal à un et il est décomposable dans K[X].

L'anneau A[X] est factoriel :

La méthode utilisée consiste à montrer que toute suite croissante d'idéaux principaux est stationnaire à partir d'un certain rang et que tout idéal engendré par un polynôme irréductible est premier.

Une suite croissante d'idéaux principaux engendrés par P_n est stationnaire à partir d'un certain rang.

Soit (c_n) la suite des contenus des polynômes P_n. Comme la suite des idéaux principaux engendrés par P_n est croissante, la suite des idéaux de A engendré par la suite (c_n) l'est aussi. Elle est donc stationnaire car A est factoriel.

Notons Q _n le polynôme primitif qui vérifie l'égalité :

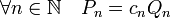
$\forall n \in \mathbb N \quad P_n = c_n Q_n\;$

Montrons que la suite (Q _n) est aussi stationnaire. Si m est plus grand que n alors P_m divise P_n, on en déduit que la suite des degrés de P_n et donc de Q_n est décroissante, elle est en conséquence stationnaire à partir d'un certain rang car toute suite décroissante d'entiers positifs est stationnaire à partir d'un certain rang.

Soit μ un entier tel que la suite des contenus et des degrés soit stationnaire à partir de μ. Montrons que la suite (Q _n) l'est aussi. Comme la suite des contenus est stationnaire, si n est plus grand que μ, Q _n divise Q _μ, comme ils sont tous les deux de même degré, ils sont proportionnels. Comme ils sont tous deux primitifs, ils sont égaux à un facteur inversible près.

Un idéal engendré par un polynôme irréductible est premier :

Soit P lun polynôme irréductible. L'objectif est de montrer que si P divise un produit Q.R il divise soit Q soit R, ce qui signifie que l'idéal engendré par P est premier.

Si P est constant égal à p un élément irréductible de A, il divise le contenu des produits de Q et R et donc le produit des contenus. Comme p est irréductible et que l'anneau A est factoriel p divise soit le contenu de Q soit celui de R, P divise donc soit Q soit R.

Si P est primitif irréductible dans K[X] et non constant, soit Q soit R est un polynôme constant. Le contenu de ce polynôme constant divise celui de P qui est primitif, ce polynôme constant est donc inversible dans A et le polynôme associé inversible dans A[X], ce qui termine la démonstration.

Soit n un entier strictement positif, l'anneau A[X₁, ..., X_n] est factoriel :

Montrons cette proposition par récurrence sur n le nombre d'indéterminées. Si n est égal à un ce théorème est l'expression de la dernière proposition.

Si le résultat est démontrée à l'ordre n - 1, l'anneau A[X₁, ..., X_{n - 1}] est factoriel. En conséquence l'anneau A[X₁, ..., X_{n - 1}][X_n] l'est aussi. L'isomorphisme d'anneau entre A[X₁, ..., X_{n - 1}][X_n] et A[X₁, ..., X_n] permet de conclure (cet isomorphisme est étudié dans l'article polynôme en plusieurs indéterminées).

Notes et références

Notes

↑ Cette définition est par exemple utilisée dans p 66 dans le site : Algèbre commutative par A. Chambert-Loir de l'Université de Rennes I
↑ La démonstration proposée s'inspire de celle donnée en page 66 du site Algèbre commutative par A. Chambert-Loir de l'Université de Rennes I
↑ Carl Friedrich Gauss Recherches arithmétiques traduction A.-C.-M. Poullet-Delisle Article 43, 1801 traduction 1807 reprit 1989 Editions Jacques Gabay
↑ On trouve ces deux définitions, par exemple sur le site Théorème de permanence de la factorialité(Gauss) par les mathématiques.net. Certains auteurs choisissent de définir uniquement le contenu d'un polynôme à coefficients dans A[X], par exemple p 73 Algèbre commutative par A. Chambert-Loir de l'Université de Rennes I
↑ La démonstration est inspirée de la page 74 du site Algèbre commutative par A. Chambert-Loir de l'Université de Rennes I
↑ Les deux dernières démonstrations s'inspirent de : Serge Lang, Algèbre, Dunod, 2004, 926 p. (ISBN 2100079808) [détail des éditions], V, §6 (éd. ang. p. 126-128)

Liens externes

(fr) Anneaux factoriels anneaux euclidiens par les mathématiques.net
(fr) Algèbre commutative par A. Chambert-Loir de l'Université de Rennes I
(fr) Cours d'agrégation interne par C. Scarcini chap 2
(fr) Anneaux factoriels par D. J. Mercier IUFM de la Guadeloupe
(fr) Quelques anneaux particuliers Site Bibmath.net 2000 - 2007

Références

(fr) Nicolas Bourbaki Eléments de mathématique. Algèbre commutative. Chapitre 8: Dimension. Chapitre 9: Anneaux locaux noethériens complets Hermann 1983 (ISBN 2225787166)
(fr) Daniel Perrin, Géométrie algébrique. Une introduction [détail des éditions]
(fr) Jean-Pierre Serre, Cours d'arithmétique [détail des éditions]
(fr) Serge Lang, Algèbre, Dunod, 2004, 926 p. (ISBN 2100079808) [détail des éditions]

Algèbre commutative

Algèbre • Anneau commutatif • Anneau euclidien • Anneau factoriel • Anneau noethérien • Anneau principal • Annulateur • Bimodule • Corps des fractions • Dual d'un module • Facteur direct • Idéal • Longueur d'un module • Module • Module simple • Module fidèle • Module libre • Module monogène • Module quotient • Module semi-simple • Produit tensoriel • Puissance extérieure

Portail des mathématiques

Ce document provient de « Anneau factoriel ».

Catégorie : Anneau

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Anneau Factoriel de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

Anneau factoriel — En mathématiques, un anneau factoriel est un cas particulier d anneau intègre. À l image des nombres entiers, il existe un équivalent du théorème fondamental de l arithmétique pour une telle structure. Tout élément d un anneau factoriel se… … Wikipédia en Français
Anneau Euclidien — Euclide (Juste de Gand ,vers 1474) En mathématiques et plus précisément en algèbre, dans le cadre de la théorie des anneaux, un anneau euclidien est un type particulier d anneau commutatif unitaire intègre. Un anneau est dit euclidien s il est… … Wikipédia en Français
Anneau (Mathématiques) — Pour les articles homonymes, voir Anneau. En algèbre générale, un anneau est une structure algébrique sur laquelle deux opérations satisfont certaines des propriétés de l addition et la multiplication des nombres. Sommaire 1 Aspect historique … Wikipédia en Français
Anneau Principal — Les anneaux principaux forment un type d anneaux important dans la théorie mathématique de la divisibilité. Ce sont les anneaux intègres (commutatifs unitaires non nuls) auxquels on peut étendre deux théorèmes qui, au sens strict, concernent l… … Wikipédia en Français
Anneau De Dedekind — Richard Dedekind définit et établit les bases de la théorie des anneaux portant maintenant son nom. En mathématiques, un anneau de Dedekind est un anneau disposant de propriétés particulières. Sa formalisation initiale a pour objectif la… … Wikipédia en Français
Anneau de dedekind — Richard Dedekind définit et établit les bases de la théorie des anneaux portant maintenant son nom. En mathématiques, un anneau de Dedekind est un anneau disposant de propriétés particulières. Sa formalisation initiale a pour objectif la… … Wikipédia en Français
Anneau Noethérien — Emmy Noether formalise les propriétés d une famille particulière d anneaux maintenant appelé anneau noethérien. En mathématique, un anneau noethérien est un cas particulier d anneau, c est à dire d un ensemble munis d une addition et d une… … Wikipédia en Français
Anneau noetherien — Anneau noethérien Emmy Noether formalise les propriétés d une famille particulière d anneaux maintenant appelé anneau noethérien. En mathématique, un anneau noethérien est un cas particulier d anneau, c est à dire d un ensemble munis d une… … Wikipédia en Français
Anneau Commutatif — Dans la théorie des anneaux, un anneau commutatif est un anneau dans lequel la loi de multiplication est commutative. Cela signifie que pour tous les éléments a et b de l’anneau, on a a*b=b*a, en notant * cette loi de multiplication. L’étude des… … Wikipédia en Français
Anneau abélien — Anneau commutatif Dans la théorie des anneaux, un anneau commutatif est un anneau dans lequel la loi de multiplication est commutative. Cela signifie que pour tous les éléments a et b de l’anneau, on a a*b=b*a, en notant * cette loi de… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Anneau Factoriel