Identité remarquable

Identité remarquable: Pour les articles homonymes, voir Identité.

En mathématiques, on appelle identités remarquables ou encore égalités remarquables certaines égalités qui s'appliquent à des nombres. Elles servent en général à accélérer les calculs, à simplifier certaines écritures, à factoriser ou à développer des expressions. Elles servent pour la résolution des équations du second degré et sont plus généralement utiles pour la recherche de solutions d'équations^{[Note 1]}.

La plupart de ces identités remarquables ont tout d'abord été démontrées à l'aide de raisonnements géométriques puis ont été généralisées à des puissances supérieures par des calculs algébriques.

Sommaire

1 Identités remarquables du second degré

1.1 Énoncés

1.2 Exemples

1.2.1 Développement et réduction

1.2.2 Équation du second degré

1.3 Polynômes au carré

1.4 Identité remarquable et géométrie

1.5 Démonstration par l'algèbre

2 Identités remarquables diverses

2.1 Identité de Brahmagupta

2.2 Identité des quatre carrés d'Euler

2.3 Identité de Sophie Germain

2.4 Identité d'Argand

2.5 Identité de Gauss

2.6 Identités de Legendre

2.7 Identités de Lagrange

3 Identités remarquables de degré n

3.1 Formule du binôme

3.2 Différence ou somme de puissances

4 Annexes

4.1 Article connexe

4.2 Liens externes

4.3 Bibliographie

4.4 Notes

4.5 Références

Identités remarquables du second degré

Énoncés

Les trois identités remarquables du second degré sont^[1] :

$(a+b)^2 = a^2 + 2ab + b^2\,$ $(a-b)^2 = a^2 - 2ab + b^2\,$ $(a-b)(a+b) = a^2 - b^2\,$

La deuxième de ces identités peut être vue comme un cas particulier de la première, en prenant, au lieu de b, -b dans la première égalité. Ces égalités font l'objet d'un vocabulaire spécifique :

Définition d'un produit remarquable^[1] — Les trois expressions suivantes sont appelées produit remarquable :
$(a+b)^2,\quad (a-b)^2\quad\text{et}\quad (a-b)(a+b)$

On définit de même :

Définition d'une somme remarquable^[1] — Les trois expressions suivantes sont appelées somme remarquable :
$a^2 + 2ab + b^2,\quad a^2 - 2ab + b^2\quad\text{et}\quad a^2 - b^2$

Ici a et b désignent des nombres, qui peuvent être des entiers, des rationnels et réels, ou même des complexes. Ces identités sont vraies dans un cadre général, elles sont aussi valables dans un anneau, à condition que a et b commutent^[2].

Exemples

Développement et réduction

Les identités remarquables permettent de transformer l'écriture de certaines expressions algébriques, comme dans l'exemple suivant^[3] :
$A=(2x - 3)^2 + (x+5)(3-x)\;$
L'expression A est la somme de deux termes. Le premier terme est un produit remarquable, que l'on peut transformer en somme :
$(2x -3)^2 = 4x^2 - 12x + 9\quad\text{et}\quad A = 4x^2 - 12x + 9 + (x+5)(3-x)\;$
Le deuxième terme se traite à l'aide de la distributivité de la multiplication par rapport à l'addition :
$(x+5)(3-x) = x(3-x)+5(3-x)=3x -x^2 + 15 - 5x = -x^2 -2x + 15\;$
En additionnant termes à termes, on obtient :

$A=4x^2 - 12x + 9-x^2 -2x + 15 = 3x^2 -14x + 24\;$

Équation du second degré

Article détaillé : Équation du second degré.

Les identités remarquables permettent de résoudre une équation du second degré. Illustrons la méthode sur l'exemple suivant :
$x^2 +2x - 5 = 0 \;$
La méthode consiste à travailler la partie de l'expression qui ne dépend pas de x de manière à utiliser une des deux premières identités remarquables et factoriser la partie qui dépend de x :
$x^2 + 2x - 5 = x^2 + 2x + 1 -6 \;$
Les trois premiers termes sont maintenant une somme remarquable, il est possible d'appliquer une identité remarquable et l'équation devient :
$x^2 + 2x - 5 = (x +1)^2 - 6 = (x +1)^2 - (\sqrt 6)^2 = 0$
On reconnaît une nouvelle somme remarquable, l'équation s'écrit encore :
$x^2 + 2x - 5 =(x+1 + \sqrt 6)(x+1- \sqrt 6)=0$
Un produit a.b de deux nombres a et b est nul si, et seulement si, a ou b est nul^{[Note 2]}. Résoudre l'équation revient à résoudre deux équations du premier degré :
$(1)\; x +1 + \sqrt 6 = 0 \quad\text{et}\quad (2)\; x +1 - \sqrt 6 = 0$
On trouve les deux solutions de l'équation, appelées aussi racines du polynômes :

$x_1 = -1 - \sqrt 6 \quad\text{et}\quad x_2 = -1 + \sqrt 6$

Polynômes au carré

Pour élever un polynôme avec un nombre quelconque de termes, ajouter les carrés de chaque terme individuellement, puis ajouter le double de la somme des produits de chaque paire possible de termes.
$(a + b + c)^2 = a^2 + b^2 + c^2 + 2 (ab + ac + bc) \,$ $(a + b + c + d)^2 = a^2 + b^2 + c^2 + d^2 + 2 (ab + ac + ad + bc + bd + cd) \,$
Identité remarquable et géométrie

Article détaillé : Algèbre géométrique.

Ces identités remarquables sont connues depuis les babyloniens^[4]. Il est possible qu'ils se soient rendus compte de ces égalités à l'aide de raisonnements géométriques. Il existe une méthode simple pour trouver la formule suivante^{[Note 3]}:
$(a+b)^2=a^2 + 2ab + b^2\;$
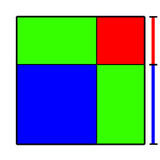
Pour se convaincre de la véracité de la formule, on considère la figure de droite. Elle représente un carré. On suppose que la longueur côté du carré bleu est égale à a et celle du carré rouge à b. L'aire du grand carré est égale à (a + b)². Il existe une autre manière d'exprimer cette aire, elle est la somme des aires bleue, rouge et des deux zones vertes. L'aire bleue est égale à a² car c'est un carré de côté a, l'aire rouge est égale à b² et chaque rectangle vert possède des côtés de longueur a et b, leur aire est égale à a.b. Comme il existe deux rectangles verts, on obtient bien la formule annoncée.

Démonstration par l'algèbre

L'algèbre permet encore de démontrer ces formules. Calculons (a - b)². La distributivité montre que :
$(a-b)^2 = (a-b)(a-b) = a(a-b) - b(a-b) = a^2 - ab - ba + b^2 = a^2 - 2ab + b^2\;$
On démontre de même la troisième identité remarquable :
$(a+b)(a-b)= a(a-b) + b(a-b) = a^2 - ab + ba - b^2 = a^2 - b^2\;$
Identités remarquables diverses

Identité de Brahmagupta

Article détaillé : Identité de Brahmagupta.

Brahmagupta, un mathématicien indien du VI^e siècle découvre une identité remarquable du quatrième degré^[5] :
$\left(a^2 - n\cdot b^2\right)\left(c^2 - n\cdot d^2\right) = \left(ac+n\cdot bd\right)^2 - n\cdot \left(ad+bc\right)^2$
Brahmagupta l'utilise dans le cas où a, b, c, d et n sont des nombres entiers. Elle permet de calculer une bonne approximation d'une racine. Pour calculer √3, il remarque que 2² - 3.1² = 1. Il applique son identité plusieurs fois, toujours avec n = 3. La première fois, il pose a = c = 2, b = d = 1. Il obtient :
$(2^2 - 3\cdot1)(2^2 - 3\cdot1)=(2\cdot2 + 3\cdot1)^2 - 3\cdot(2\cdot1 + 1\cdot2)^2= 7^2 - 3\cdot 4^2=1$
Il recommence avec cette fois avec : a = c = 7, b = d = 4. Il obtient une nouvelle manière d'écrire 1 :
$97^2 - 3\cdot 56^2 = 1$
Il réapplique la même logique, il obtient encore une autre manière d'écrire 1:
$18\,817^2 - 3\cdot 10\,864^2 = 1$
Cette égalité s'écrit encore :
$18\,817^2 = 3\cdot 10\,864^2 + 1\quad\text{et}\quad \left(\frac {18\,817}{10\,864}\right)^2 = 3 + \frac 1{10\,864^2}$
Il obtient une fraction dont le carré est presque égal à 3, ce qui revient à dire que 18 817/10 864 est presque égal à √3. Si on calcule la fraction, on trouve un résultat dont les neuf premiers chiffres significatifs fournissent la meilleure approximation possible (avec le même nombre de décimales), à savoir : 1,73205081. Il utilise aussi sa formule pour trouver des solutions à une équation diophantienne difficile, dite de Pell-Fermat. Sa méthode porte le nom de chakravala.

Identité des quatre carrés d'Euler

Article détaillé : Identité des quatre carrés d'Euler.

L'identité des quatre carrés d'Euler relie entre eux huit nombres. Elle prend la forme suivante :
$(a_1^2+a_2^2+a_3^2+a_4^2)(b_1^2+b_2^2+b_3^2+b_4^2)\,$ $=(a_1 b_1-a_2 b_2 - a_3 b_3 - a_4 b_4)^2 + (a_1 b_2 + a_2 b_1 + a_3 b_4 - a_4 b_3)^2\,$ $+\,(a_1 b_3 - a_2 b_4 + a_3 b_1 + a_4 b_2)^2 + (a_1 b_4 + a_2 b_3 - a_3 b_2 + a_4 b_1)^2\,$
Elle est utilisée, entre autres pour démontrer le théorème des quatre carrés qui indique que tout nombre entier est somme de quatre carrés.

Identité de Sophie Germain

L'identité de Sophie Germain énonce que pour tous nombres x et y, on a :
$x^4+4y^4 = ((x+y)^2+y^2)((x-y)^2+y^2) = (x^2+2xy+2y^2)(x^2-2xy+2y^2) \,$
Identité d'Argand
$(x^2+x+1)(x^2-x+1) = x^4+x^2+1 \,$
Identité de Gauss
$a^3+b^3+c^3-3abc = (a+b+c)(a^2+b^2+c^2-ab-ac-bc) = \frac{1}{2} (a+b+c)[(a-b)^2+(b-c)^2+(a-c)^2] \,$
Identités de Legendre
$(a+b)^2+(a-b)^2=2(a^2+b^2) \,$ $(a+b)^2-(a-b)^2=4ab \,$ $(a+b)^4-(a-b)^4=8ab(a^2+b^2) \,$
Identités de Lagrange
$(a^2+b^2)(x^2+y^2) = (ax+by)^2+(ay-bx)^2 \,$ $(a^2+b^2+c^2)(x^2+y^2+z^2) = (ax+by+cz)^2+(ay-bx)^2+(az-cx)^2+(bz-cy)^2 \,$
La première identité de Lagrange ici listée est un cas particulier de l'identité de Brahmagupta.

Identités remarquables de degré n

Formule du binôme

Article détaillé : Formule du binôme.

La même technique de démonstration que celle utilisé pour les formules de degré 2 montre que, si a et b désignent toujours deux nombres :
$(a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3\,$ $(a - b)^3 = a^3 - 3a^2b + 3ab^2 - b^3\,$
Appliqué encore une fois, on obtient :
$(a + b)^4 = a^4 + 4a^3b + 6a^2b^2 +4ab^3 + b^4\,$ $(a - b)^4 = a^4 - 4a^3b + 6a^2b^2 -4ab^3 + b^4\,$
On peut la généraliser à un degré n quelconque, à l'aide de la formule du binôme :
$(x+y)^n=\sum_{k=0}^n {n \choose k} x^{n-k} y^k$
Les coefficients de l'expression, considérée comme un polynôme en x et en y sont appelés coefficients binomiaux. Comme b peut prendre une valeur négative, on obtient bien les deux formes précédentes.

La formule s'applique même si a et b ne sont pas des nombres. Ces lettres peuvent désigner deux matrices qui commutent entre elles. De manière générale, la formule est vraie dans un anneau, si a et b commutent.

Différence ou somme de puissances

Il est aussi possible de généraliser la troisième identité remarquable de degré 2. Si a et b désignent deux nombres :
$a^3 + b^3 = (a + b) (a^2 - ab + b^2)\,$ $a^3 - b^3 = (a - b) (a^2 + ab + b^2) \,$ $a^4 + b^4 = (a^2 + ab\sqrt{2}+ b^2 ) (a^2 - ab\sqrt{2} + b^2 )\,$
Si l'on travaille dans un ensemble qui n'est pas celui des nombres, la dernière formule n'est valable que si √2 existe, c'est-à-dire s'il existe une valeur c telle que c² soit égal à 1 + 1. Il faut, en conséquence que l'élément neutre de la multiplication existe.

La formule suivante permet de généraliser la démarche :
$a^n - b^n = (a - b) (a^{n-1} + a^{n-2}b + \cdots + ab^{n-2} + b^{n-1} ) \,$ $a^n - b^n = (a - b)\sum_{k=0}^{n-1} a^{(n-1-k)} b^k$
Annexes

Article connexe

Livre II des Éléments d'Euclide

Liens externes

Identités remarquables de degré supérieur à 2, sur le site de G. Villemin

Identités remarquables (Flash), sur le site de Sésamath

Bibliographie

R. Brault, Mathématiques 3^ième, Hachette éducation, 2008 (ISBN 978-2-01-125539-6)
La première partie de l'article s'inspire largement de cette référence.

(en) Leonard Eugene Dickson, History of the Theory of Numbers [détail des éditions], vol. II, Diophantine analysis
Les deux identités remarquables, ainsi que leurs usages en arithmétique sont présents dans cette référence, beaucoup plus technique que la précédente.

Notes

↑ Ces informations ainsi que celles de l'article sont essentiellement extraites du livre : R. Brault Mathématiques 3^ième Hachette éducation (2008) (ISBN 978-2-01-125539-6)

↑ Voir à ce sujet l'article Équation produit-nul

↑ Les autres formules sont proposées dans l'article Algèbre géométrique

Références

↑ ^{a, b et c} Écriture littérale et identités remarquables par le site Wouf

↑ Les éléments pour fournir ces identités sont disponibles dans : A. Chambert-Loir, Algèbre commutative, 2005, Université de Rennes I, chap. 2

↑ Il est extrait de la page d'Y. Monka Développements, sur le site M@th et tiques, p. 2

↑ A. Dahan-Dalmedico et J. Peiffer, Une Histoire des mathématiques - Routes et dédales [détail des éditions] , p 74

↑ (en) John J. O’Connor et Edmund F. Robertson, « Pell's equation », dans MacTutor History of Mathematics archive, université de St Andrews [lire en ligne] .

Portail des mathématiques

Catégories :
Identité mathématique
Mathématiques élémentaires

Contenu soumis à la licence CC-BY-SA. Source : Article Identité remarquable de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

Identite remarquable (mathematiques elementaires) — Identité remarquable Pour les articles homonymes, voir Identité. En mathématiques, on appelle identités remarquables ou encore égalités remarquables certaines égalités qui s appliquent à des nombres. Elles servent en général à accélérer les… … Wikipédia en Français
Identité remarquable (maths élém) — Identité remarquable Pour les articles homonymes, voir Identité. En mathématiques, on appelle identités remarquables ou encore égalités remarquables certaines égalités qui s appliquent à des nombres. Elles servent en général à accélérer les… … Wikipédia en Français
Identité remarquable (mathématiques élémentaires) — Identité remarquable Pour les articles homonymes, voir Identité. En mathématiques, on appelle identités remarquables ou encore égalités remarquables certaines égalités qui s appliquent à des nombres. Elles servent en général à accélérer les… … Wikipédia en Français
Identite (mathematiques) — Identité (mathématiques) Pour les articles homonymes, voir identité. Ne doit pas être confondu avec égalité (mathématiques) ou équation. En mathématiques et plus généralement dans les domaines scientifiques, une identité est la constatation … Wikipédia en Français
IDENTITÉ — Gottlob Frege (1894) a observé que l’identité est indéfinissable: «Puisque toute définition est une identité, l’identité elle même ne saurait être définie.» Le même (to auto , idem ) appartient à la liste des «transcendantaux» médiévaux, c’est à… … Encyclopédie Universelle
Identite — Identité Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom … Wikipédia en Français
Identite trigonometrique — Identité trigonométrique Une identité trigonométrique est une relation impliquant des fonctions trigonométriques et qui est vérifiée pour toutes les valeurs des variables intervenant dans la relation. Ces identités peuvent être utiles quand une… … Wikipédia en Français
Identité Trigonométrique — Une identité trigonométrique est une relation impliquant des fonctions trigonométriques et qui est vérifiée pour toutes les valeurs des variables intervenant dans la relation. Ces identités peuvent être utiles quand une expression comportant des… … Wikipédia en Français
Identité (mathématiques) — Pour les articles homonymes, voir identité. Ne doit pas être confondu avec égalité (mathématiques) ni équation. En mathématiques et plus généralement dans les domaines scientifiques, une identité est la constatation que deux objets… … Wikipédia en Français
Identité — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Identité », sur le Wiktionnaire (dictionnaire universel) Sens généraux L identité désigne, en… … Wikipédia en Français

Mark and share
Search through all dictionaries
Translate…
Search Internet

Share the article and excerpts