Parabole

Pour les articles homonymes, voir Parabole (homonymie).

Une parabole

La parabole est l'intersection d'un plan avec un cône de révolution lorsque le plan est parallèle à l'une des génératrices du cône. Elle est un type de courbe dont les nombreuses propriétés géométriques ont intéressé les mathématiciens dès l'Antiquité et ont reçu des applications techniques variées.

Sommaire

1 Mathématiques
2 Applications
- 2.1 Physique
- 2.2 Ondes hertziennes et lumière
3 Voir aussi
- 3.1 Articles connexes
- 3.2 Liens externes

Mathématiques

Section conique

Les paraboles font partie de la famille des coniques, c'est-à-dire des courbes qui s'obtiennent par l'intersection d'un cône de révolution avec un plan ; en l'occurrence, la parabole est obtenue lorsque le plan est parallèle à l'une des génératrices du cône.

La parabole est l'intersection d'un plan avec un cône de révolution lorsque le plan est parallèle à une des génératrices du cône

Directrice, foyer et excentricité

Soient $D$ une droite et $F$ un point n'appartenant pas à $D$ , et soit $P$ le plan contenant la droite $D$ et le point $F$ ). On appelle parabole de droite directrice $D$ et de foyer $F$ l'ensemble des points $M$ du plan $P$ vérifiant

$\frac{d(M,F)}{d(M,D)} = 1$

où $d (M, F)$ mesure la distance du point $M$ au point $F$ et $d (M, D)$ mesure la distance du point $M$ à la droite $D$ . C'est donc une conique dont l'excentricité $e$ vaut 1

Équations

À partir du foyer et de la directrice

Si la parabole est donnée par son foyer $F$ et sa directrice $\mathcal D$ , on appelle $O$ le projeté orthogonal de $F$ sur $\mathcal D$ , on appelle $p$ (paramètre de la parabole) la distance $O F$ et on appelle $S$ le milieu de $[F O]$ . Alors, dans le repère orthonormé $(S,\vec i, \vec j)$ où $\vec j$ a même direction et sens que $\overrightarrow{OF}$ , l'équation de la parabole est

$y = \frac{x^2}{2p}$

À partir de la fonction du second degré

Article détaillé : fonction du second degré.

La courbe représentative d'une fonction polynôme du second degré d'équation

y = a x 2 + b x + c

où $a,\,b$ et $c$ sont des constantes réelles ( $a$ non nul), est une parabole. Dans le cas $a = 1$ , $b = 0$ , et $c = 0$ on obtient une expression simple pour une parabole: $y = x 2$ .

Le sommet $S$ d'une parabole est le point de coordonnées $\left(- \tfrac{b}{2a}; -\tfrac{b^2 - 4ac}{4a}\right)$ . Son axe de symétrie est l'axe $(S\vec j)$ . Dans le repère $(S,\vec i, \vec j)$ , son équation est

Y = a X 2

Son foyer est le point $F\left(0;\tfrac{1}{4a}\right)$ et sa directrice est la droite $\mathcal D$ d'équation $Y = - \frac{1}{4a}$

Démonstration

Dans le repère $(S,\vec i, \vec j)$ , on considère

$F\left(0;\tfrac{1}{4a}\right)$

$\mathcal D : Y = - \frac{1}{4a}$ .

Soit $M (X; Y)$ , on calcule directement la distance d du point $M$ à la droite $\mathcal D$ :

$d = \left|Y + \frac{1}{4a}\right|$

On calcule alors la distance d' = FM :

$d' = \sqrt {\left( Y - \frac{1}{4a} \right)^2 + X^2}$

On interprète, par équivalence, la condition $d = d'$

$d=d' \Longleftrightarrow d^2=d'^2 \Longleftrightarrow \left( Y + \frac{1}{4a} \right)^2 = \left( Y - \frac{1}{4a} \right)^2 + X^2$

$d=d' \Longleftrightarrow \dfrac{Y}{a}=X^2 \Longleftrightarrow Y=aX^2$

Donc

$d=d' \Longleftrightarrow M \in \mathcal P:Y=aX^2$

À partir de l'équation générale

Soit l'équation $A x 2 + 2 B x y + C y 2 + 2 D x + 2 E y + F = 0$ , dans un repère orthonormal. Si $B 2 - A C = 0$ alors cette équation est celle d'une parabole ou de deux droites parallèles.

Soit l'équation $A x 2 + C y 2 + 2 D x + 2 E y + F = 0$ , dans un repère orthonormal. Si $A C = 0$ avec $A E$ ou $D C$ non nul alors cette équation est celle d'une parabole.

Enfin, dans tout repère orthonormal, l'équation d'une parabole est de la forme

A x 2 + 2 B x y + C y 2 + 2 D x + 2 E y + F = 0

avec

B 2 - A C = 0

Équation polaire

Dans le repère polaire $(O, \vec e_{r}, \vec e_{\theta})$ où O est le foyer de la parabole et l'axe polaire en est l'axe focal, l'équation de la parabole est $\overrightarrow{r} = \overrightarrow{OP} = \frac{p}{1+\cos(\theta)} \vec e_{r}$ .

Paramétrisation

Dans le repère cartésien $(O, \vec i, \vec j)$ où $O$ est le point situé au milieu du segment constitué du foyer $F$ et de sa projection $H$ sur la directrice et où $\vec j$ est un vecteur unitaire orienté de $O$ vers $F$ , on peut envisager plusieurs paramétrisations de la parabole :

Une paramétrisation cartésienne par l'abscisse : $\overrightarrow{OP}(x)=x\vec i+\frac{x^2}{2p}\vec j$ , pour tout $x\in\R$
Une paramétrisation cartésienne par l'ordonnée : $\overrightarrow{OP}(y)=(\pm\sqrt{2py})\vec i+y\vec j$ , pour tout $y\in\R^+$
Des paramétrisations cartésiennes dépendant chacune d'un constante arbitraire a>0 : $\overrightarrow{OP}(t)=2pat\vec i+2pa^2t^2\vec j=2pa(t\vec i+at^{2}\vec j)$ , pour tout $t\in\R$

(Pour a=1/(2p) on retrouve la paramétrisation par l'abscisse.) Ces paramétrisations sont régulières (i.e. le vecteur dérivé ne s'annule pas). Le vecteur $(1,2 a t)$ dirige alors la tangente au point de paramètre $t$ .

Quelques propriétés géométriques de la parabole

Cordes parallèles

Toutes les cordes parallèles ont leur milieu situé sur une droite perpendiculaire à la directrice. La tangente parallèle à cette direction a son point de contact sur cette droite. Les deux tangentes à la parabole aux extrémités d'une telle corde se coupent sur cette droite.

Tangente et bissectrice

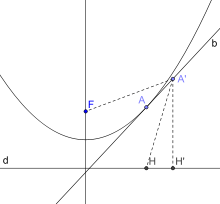
Si A est un point sur une parabole définie par un foyer F et une directrice (d), alors la tangente de la parabole en A est la bissectrice intérieure de l'angle formée par F, A et le projeté orthogonal de A sur (d).

Éléments de démonstration

(d) est la tangente en A et la bissectrice de l'angle (FAH)

Soit H le projeté orthogonal de A sur (d), (b) la bissectrice de l'angle FÂH.

On sait que la parabole découpe le plan en deux zones : l'une, contenant F, regroupe les points M pour lesquels FM < FM_H et l'autre, contenant (d), regroupe les points M pour lesquels FM > FM_H. On montre que (b) est la tangente en A à la parabole en prouvant qu'elle est entièrement incluse (excepté le point A) dans la zone vérifiant FM > FM_H.

Le triangle FAH est isocèle en A par définition de la parabole. Donc (b) est aussi la médiatrice de [FH].

Soit A' un point sur (b) distinct de A. A' appartient donc à la médiatrice de [FH] et A'F = A'H.

Soit H' le projeté orthogonal de A' sur (d). Le triangle HH'A' est rectangle en H' donc A'H' < A'H.

Donc finalement A'H' < A'F. Donc A' est dans la partie du plan vérifiant FM > FM_H.

La droite (b) est entièrement incluse dans cette zone (sauf au point A), c'est donc la tangente à la parabole en A.

Une démonstration purement analytique est possible. Dans le repère $(S,\vec i, \vec j)$ , l'équation de la parabole est

y = a x 2

La tangente au point d'abscisse m a pour vecteur directeur

$\vec u(1,2am)$

Les points F et H ont pour coordonnées respectives

$F\left(0;\frac1{4a}\right)$ et $H\left(m;-\frac1{4a}\right))$

La droite (HF) a pour vecteur directeur

$\vec v\left(m;-\frac1{2a}\right)$

elle est donc orthogonale à la tangente.

La tangente est donc hauteur du triangle isocèle AFH, c'est donc bien la bissectrice de l'angle FÂH.

Propriété relative à l'orthoptique

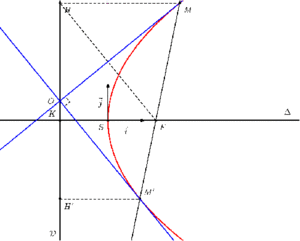
En se déplaçant le long de sa directrice, la parabole est toujours vue sous un angle droit.

Soient $M$ et $M'$ les points d'intersection d'une droite quelconque passant par le foyer de la parabole avec la parabole. Les deux tangentes de la parabole passant par $M$ et $M'$ se coupent sur la directrice en formant un angle droit entre elles. De plus, si on appelle $H$ et $H'$ les projetés respectifs de $M$ et $M'$ sur la directrice et $O$ le point d'intersection des deux tangentes et de la directrice, alors $O$ est le milieu de $[H H']$ .

En se déplaçant le long de sa directrice, la parabole est toujours vue sous un angle droit.

Démonstration

On note O le point d'intersection des deux tangentes. Pour des notations plus simples des angles, on note

$\alpha = \widehat {FMO}$ et $\beta = \widehat {FM'O}$ .

D'après la corrélation montrée plus haut entre tangente et bissectrice, on a :

$\widehat {FMH} = 2 \alpha$

$\widehat {FM'H'} = 2 \beta$

Puisque les droite (HM) et (H'M') sont paralllèes les deux angles précédents, découpés par (MM') sur ces droites, sont supplémentaires. On a donc :

$2 \beta + 2 \alpha = \pi \Leftrightarrow \beta + \alpha = \frac {\pi}{2}$

On en déduit directement avec la somme des angles d'un triangle :

$\widehat {MOM'} = \pi - \left(\alpha + \beta \right) = \frac {\pi}{2}$

On appelle P le point d'intersection de la perpendiculaire à (MM') passant F avec la directrice. Les triangles FMP et HMP sont égaux car FM=HM donc le point P est sur la bissectrice de l'angle FMH, il est donc sur la tangente passant M. De même le point P est sur la tangente passant par M'. Le point P est donc aussi le point O d'intersection des deux tangentes qui se trouve donc bien sur la directrice.

Les deux tangentes se coupent donc en angle droit sur la directrice.

Enfin, les égalités, FP=HP et FP=H'P, prouvent que P donc O est le milieu de [HH'].

Applications

Physique

trajectoire parabolique

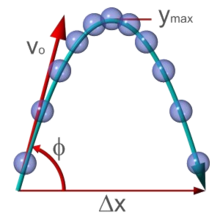
La parabole est la trajectoire décrite par un objet que l'on lance si on peut négliger la courbure de la Terre, le frottement de l'air (vent, ralentissement de l'objet) et la variation de la gravité avec la hauteur.

Torricelli a démontré (1640) que l'enveloppe de ces trajectoires est elle-même une parabole : parabole de sûreté.

Ondes hertziennes et lumière

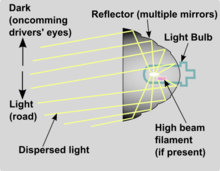
Par métonymie, une parabole désigne une antenne parabolique. Il s'agit plus exactement d'une application des propriétés de la surface nommée paraboloïde de révolution.

Principe du phare automobile à miroir parabolique

Les paraboloïdes permettent soit de concentrer des ondes ou des rayons en un point, le foyer de la parabole (c'est cette propriété qui est utilisée par les antennes), soit inversement de diffuser sous forme d'un faisceau cylindrique la lumière produite par une ampoule au foyer de la parabole (propriété exploitée par un projecteur ou un phare).

Un cylindre parabolique permet, de même, de concentrer la lumière sur une droite, par exemple dans des concentrateurs solaires

Voir aussi

Liens externes

Cours de géométrie de M. Gerhard Wanner de l'université de Genève, section de mathématiques
Les théorèmes "belges" - Coniques et théorème de Dandelin
Lancement du poids - Parabole de sureté

v · courbes
Coniques (cercle, ellipse, parabole, hyperbole)
Cardioïde • Cissoïde • Clothoïde • Conchoïde • Cycloïde • Épicycloïde • Folium de Descartes • Hélice Hypocycloïde (astroïde, deltoïde) • Hypotrochoïde • Néphroïde • Spirale (d'Archimède, logarithmique) • Strophoïde
Lemniscates (lemniscate de Gerono, lemniscate de Booth, lemniscate de Bernoulli, courbe du diable)
Trajectoire • Ovale de Cassini • Chaînette • Courbe brachistochrone

Portail de la géométrie

Catégorie :

Conique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Parabole de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

PARABOLE — PARABOLE, religion Récit allégorique, habituellement assez bref, sous lequel, dans les textes néo testamentaires et spécialement dans les Évangiles, se cache un enseignement, selon un procédé populaire et oriental consistant à faire passer un… … Encyclopédie Universelle
parabole — 1. (pa ra bo l ) s. f. Allégorie qui renferme quelque vérité importante. La parabole a deux parties, le corps et l âme ; le corps est le récit de l histoire qu on a imaginée ; et l âme, le sens moral ou mystique, caché sous les paroles ou récit.… … Dictionnaire de la Langue Française d'Émile Littré
parabole — PARABOLE. s. f. Similitude & allegorie sous laquelle on envelope quelque verité importante. Il n a guere d usage qu en parlant des similitudes dont l Ecriture sainte se sert. Une belle parabole. les paraboles de l Evangile. Nostre Seigneur s est… … Dictionnaire de l'Académie française
parabolé — parabolé, ée (entrée créée par le supplément) (pa ra bo lé, lée) adj. Qui est en forme de parabole. Réflecteurs parabolés de l Arc de triomphe … Dictionnaire de la Langue Française d'Émile Littré
parabole — (n.) 1580s, from Gk. parabole comparison (see PARABLE (Cf. parable)) … Etymology dictionary
parabole — parabolė statusas T sritis fizika atitikmenys: angl. parabola vok. Parabel, f rus. парабола, f pranc. parabole, f … Fizikos terminų žodynas
parabolė — statusas T sritis fizika atitikmenys: angl. parabola vok. Parabel, f rus. парабола, f pranc. parabole, f … Fizikos terminų žodynas
Parabole — Pa*rab o*le, n. [L., fr. Gr. ?. See {Parable}.] (Rhet.) Similitude; comparison. [1913 Webster] … The Collaborative International Dictionary of English
parabolė — parãbolė dkt. Senẽlis mėgsta kùrti parãboles … Bendrinės lietuvių kalbos žodyno antraštynas
parabole — Parabole, Parabola, Comparatio, Collatio, Simile … Thresor de la langue françoyse

Dictionnaires et Encyclopédies sur 'Academic'

Parabole

Sommaire