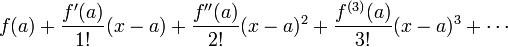Serie de Taylor

Serie de Taylor

Série de Taylor

Page d'aide sur l'homonymie Pour les articles homonymes, voir Taylor.
Brook Taylor,
Celui dont la série porte le nom.

En analyse, la série de Taylor se définit pour une fonction f indéfiniment dérivable d'une variable réelle ou complexe et en un point a au voisinage duquel la fonction est définie. La série de Taylor de f en a est la série entière suivante :

f(a)+\frac{f'(a)}{1!}(x-a)+\frac{f''(a)}{2!}(x-a)^2+\frac{f^{(3)}(a)}{3!}(x-a)^3+\cdots\,

ce qui s'écrit sous forme synthétique comme suit :

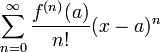\sum_{n=0}^{\infin} \frac{f^{(n)}(a)}{n!}(x-a)^{n}.

n! est la factorielle de n (le produit de tous les entiers naturels inférieurs ou égal à n) et f (n)(a) désigne la dérivée nème de f au point a. La notation fait encore sens en analyse fonctionnelle dans les algèbres normées, réelles ou complexes ; mais cette généralisation ne sera pas plus abordée dans cet article.

Si a = 0, la série est aussi appelée une série de Maclaurin.

Fonctions usuelles

Nom de la fonction : Série de Taylor: Rayon de convergence :
Exponentielle ex = 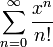\sum^{\infty}_{n=0}\frac{x^n}{n!} Infini
Logarithme ln(1 + x) = 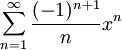\sum^{\infin}_{n=1}\frac{(-1)^{n+1}}n x^n 1
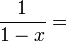
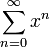
Somme d'une série géométrique \frac{1}{1-x} = \sum^{\infin}_{n=0}x^n 1
Fonctions trigonométriques : sin(x) = 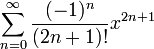\sum^{\infin}_{n=0}\frac{(-1)^n}{(2n+1)!}x^{2n+1} Infini
cos(x) = 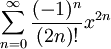\sum^{\infin}_{n=0} \frac{(-1)^n}{(2n)!} x^{2n} Infini
tan(x) = 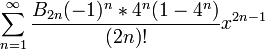\sum^{\infin}_{n=1} \frac{B_{2n} (-1)^n*4^n (1-4^n)}{(2n)!} x^{2n-1} Pi / 2
sec(x) = 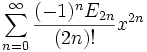\sum^{\infin}_{n=0} \frac{(-1)^n E_{2n}}{(2n)!} x^{2n} Pi / 2
arcsin(x) = 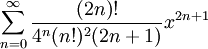\sum^{\infin}_{n=0}\frac{(2n)!}{4^n (n!)^2 (2n+1)} x^{2n+1} 1
arccos(x) = 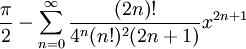\frac{\pi}{2} - \sum^{\infin}_{n=0}\frac{(2n)!}{4^n (n!)^2 (2n+1)} x^{2n+1} 1
arctan(x) = 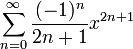\sum^{\infin}_{n=0}\frac{(-1)^n}{2n+1}x^{2n+1} 1
Fonctions hyperboliques : sh(x) = 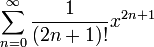\sum^{\infin}_{n=0}\frac{1}{(2n+1)!}x^{2n+1} Infini
ch(x) = 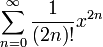\sum^{\infin}_{n=0}\frac{1}{(2n)!}x^{2n} Infini
th(x) = 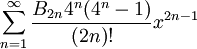\sum^{\infin}_{n=1}\frac{B_{2n} 4^n(4^n-1)}{(2n)!} x^{2n-1} Pi / 2
argsh(x) = 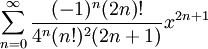\sum^{\infin}_{n=0}\frac{(-1)^n (2n)!}{4^n(n!)^2 (2n+1)} x^{2n+1} 1
argch(x) = 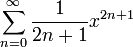\sum^{\infin}_{n=0}\frac{1}{2n+1}x^{2n+1} 1
Fonction W de Lambert W(x) = 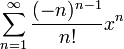\sum^{\infin}_{n=1}\frac{(-n)^{n-1}}{n!} x^n 1 / e

|Notations --- Dans les séries de Taylor ci-dessus, on a utilisé les notations suivantes :

Convergence de la série de Taylor

La série de Taylor est une série entière. Elle admet donc un rayon de convergence R, et sur le disque de centre a et de rayon R, la série converge normalement sur tout compact. Cependant,

  • La somme de la série de Taylor de f en a sur son disque de convergence peut être différente de la fonction f ;
  • Le rayon de convergence ne donne en général pas plus de renseignements sur la taille du domaine de définition de f.

Par exemple, toutes les dérivées de f définie par f(x)  =  exp(-1/x2) sont nulles en x = 0, et donc la somme de sa série de Taylor de f est nulle, et ainsi son rayon de convergence est infini, alors que la fonction n'est pas du tout nulle. Ce phénomène arrive pour des fonctions plates (toutes les dérivées successives en un point s'annulent).

Si la fonction f vaut la somme de sa série entière au voisinage de a, alors on dit que f est analytique. Cette définition est valable aussi bien pour les fonctions d'une variable réelle que pour les fonctions d'une variable complexe. Toutefois, une fonction d'une variable complexe analytique est appelée holomorphe : pour qu'elle le soit, il suffit de la supposer dérivable ! C'est un des premiers résultats de rigidité en analyse complexe.

Les sommes partielles d'une série de Taylor peuvent être utilisées pour calculer des valeurs approchées de la fonction au voisinage d'un point.

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « S%C3%A9rie de Taylor ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Serie de Taylor de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Série de taylor — Pour les articles homonymes, voir Taylor. Brook Taylor, Celui dont la série porte le nom. En analyse, la série de Taylor …   Wikipédia en Français

  • Serie de Taylor — sin(x) y aproximaciones de Taylor centradas en 0, con polinomios de grado 1, 3, 5, 7, 9, 11 y 13. En matemáticas, una serie de Taylor de una función f(x) infinitamente derivable (real o compleja) defin …   Wikipedia Español

  • Série de Taylor — Pour les articles homonymes, voir Taylor. En mathématiques, et plus précisément en analyse, la série de Taylor d une fonction f (au voisinage d un point a) est une série entière construite à partir de f et de ses dérivées successives en a …   Wikipédia en Français

  • Serie de Taylor — En matemáticas, la serie de Taylor de formula función f infinitamente derivable (real o compleja) definida en un intervalo abierto (a r, a+r) se define con la siguiente suma: Aquí …   Enciclopedia Universal

  • série de Taylor — Teiloro eilutė statusas T sritis fizika atitikmenys: angl. Taylor series vok. Taylorsche Reihe, f rus. ряд Тэйлора, m pranc. série de Taylor, f; série taylorienne, f …   Fizikos terminų žodynas

  • Développement en série de Taylor — Série de Taylor Pour les articles homonymes, voir Taylor. Brook Taylor, Celui dont la série porte le nom. En analyse, la série de Taylor …   Wikipédia en Français

  • Série de MacLaurin — Série de Taylor Pour les articles homonymes, voir Taylor. Brook Taylor, Celui dont la série porte le nom. En analyse, la série de Taylor …   Wikipédia en Français

  • Série numérique — Série (mathématiques) Pour les articles homonymes, voir Série. En mathématiques, la série constitue une généralisation de la notion de somme, pour une succession infinie de termes. L étude des séries consiste à effectuer la somme d un nombre fini …   Wikipédia en Français

  • Série semi-convergente — Série (mathématiques) Pour les articles homonymes, voir Série. En mathématiques, la série constitue une généralisation de la notion de somme, pour une succession infinie de termes. L étude des séries consiste à effectuer la somme d un nombre fini …   Wikipédia en Français

  • Serie entiere — Série entière Pour les articles homonymes, voir Entier (homonymie). En mathématiques et particulièrement en analyse, une série entière est une série de fonctions de la forme où les coefficients an forment une suite réelle ou complexe. La série… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”