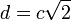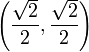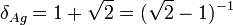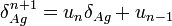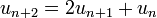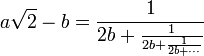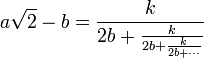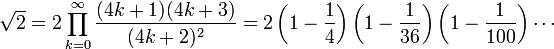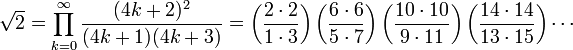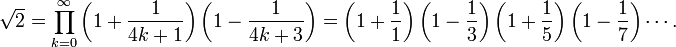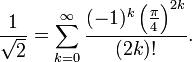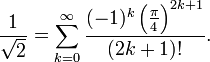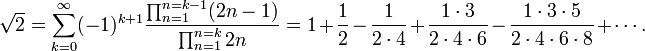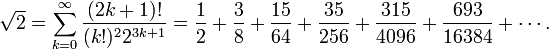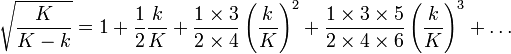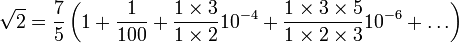Constante de Pythagore

La racine carrée de deux, notée √2, √2 ou 2^1/2, est définie comme le seul nombre réel positif qui, lorsqu'il est multiplié par lui-même, donne le nombre 2, autrement dit √2 × √2 = 2. C'est un nombre irrationnel, dont une valeur approchée est

1,414 213 562 373 095 048 801 688 724 209 698 078 569 671 875 376 948 073 176 679 737 990 732 478

Le calcul d'une valeur approchante de √2 a été un problème mathématique pendant des siècles. Ces recherches ont permis de perfectionner les algorithmes de calculs d'extraction de racines carrées. En informatique, ces recherches se sont poursuivies afin d'optimiser ces algorithmes en réduisant les temps de calcul et la consommation de mémoire^[1].

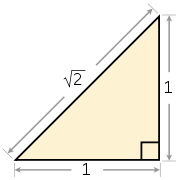
La longueur √2 peut être construite géométriquement de plusieurs manières; par exemple, par le théorème de Pythagore, l'hypoténuse d'un triangle rectangle isocèle de côté 1 vaut √2.

Il est vraisemblable que √2 ait été le premier nombre reconnu comme irrationnel, c'est-à-dire ne pouvant être exprimé comme une fraction de nombres entiers. La découverte des nombres irrationnels est généralement attribuée à l'école de Pythagore, dont l'un des membres aurait produit la toute première démonstration d'irrationalité. Sans pouvoir affirmer avec certitude que celle-ci concernait √2, le fait que les propriétés de ce nombre soient connues et étudiées depuis très longtemps, et aussi qu'il est particulièrement simple d'en démontrer l'irrationalité, est un argument pour faire de √2 « le premier irrationnel ».

Le nombre intervient dans des applications de la vie courante :

• les feuilles de papier au format international (ISO 216) ont une proportion longueur/largeur égale à √2 ;
• en musique, le rapport des fréquences de la quarte augmentée de la gamme tempérée vaut √2 ;
• en électricité, la tension maximale du courant alternatif domestique vaut √2 de la tension efficace indiquée (généralement 110 ou 220 V) ;
• en photographie, la suite des valeurs d'ouverture du diaphragme sont les valeurs approchées d'une suite géométrique de raison √2.

Sommaire 1 Étymologie 2 √2 dans la vie courante 2.1 Format de papier 2.2 Musique 2.3 Électricité 2.4 Photographie 3 Histoire 3.1 Babylone 3.2 Grèce antique 3.3 Monde indien 3.4 Monde musulman 3.5 Occident 4 Géométrie 4.1 Duplication du carré 4.2 Triangle rectangle isocèle 4.3 Trigonométrie 4.4 Construction de √2 à la règle et au compas 4.5 Construction de √2 au compas seul 5 Propriétés mathématiques principales 5.1 Irrationalité 5.1.1 Démonstration géométrique 5.1.2 Démonstration arithmétique 5.2 Normalité 5.3 Degré algébrique et degré d'irrationalité 5.4 Proportion d'argent 5.5 Développement en fraction continue 5.6 Développements en série et produit infini 5.6.1 Produits infinis 5.6.2 Séries 6 Méthodes numériques d'approximation 6.1 Méthodes à convergence linéaire 6.1.1 Méthode de Théon de Smyrne 6.1.2 Solutions de l'équation diophantienne a²− 2b² = k 6.1.3 Méthode de Théon généralisée 6.1.4 Développement en fraction continue 6.1.5 Développement de Taylor 6.1.6 Dichotomie 6.2 Méthode à convergence quadratique 6.3 Méthodes cubiques 6.3.1 Méthode de Halley 6.3.2 Méthode de Householder 6.4 Méthodes d'ordre supérieur 7 Notes et références 8 Bibliographie 9 Voir aussi 9.1 Articles connexes 9.2 Liens externes

Étymologie

L'expression « racine carrée » est issue de la notation géométrique européenne qui prévalait avant la notation algébrique, et plus particulièrement de l'une des constructions de √2 présentée au paragraphe précédent. L'expression « radical de deux » était aussi utilisée.

Les problèmes mathématiques ont souvent été présentés sous forme géométrique avant d'être ramenés à des expressions algébriques.

√2 dans la vie courante

Format de papier

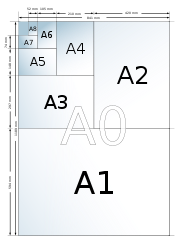
Les formats de papier A, B et C de la norme ISO 216, d'emploi courant hors de l'Amérique du Nord, ont été conçus pour vérifier une propriété remarquable : une feuille coupée en deux parties égales par la largeur, produit deux feuilles homothétiques à l'original ; c'est-à-dire avec le même rapport longueur/largeur. L'aire étant diminuée d'un facteur 2, ceci n'est possible que si ce rapport vaut √2 ; dans la pratique, les dimensions sont arrondies.

Ci-dessous sont données les valeurs approximatives des formats A0 à A5 en fonction de √2.

Valeurs approximatives des dimensions des formats A0 à A5 exprimées en fonction de √2. Dans la pratique, les dimensions sont arrondies.

format	longueur (m)	largeur (m)	aire (m²)
A0	√√2	√√2/√2	1
A1	√√2/√2	√√2/2	1/2
A2	√√2/2	√√2/(2√2)	1/4
A3	√√2/(2√2)	√√2/4	1/8
A4	√√2/4	√√2/(4√2)	1/16

Les séries B et C diffèrent de la série A respectivement d'un facteur √√2 (~ 1,19) et √√√2 (~ 1,09).

Les facteurs d'agrandissement de 200%, 141%, 71%, 50% proposés par les photocopieuses sont des approximations de (√2)ⁿ qui permettent le passage à des formats de papier supérieurs ou inférieurs — que ce soit physiquement ou par impression de 2ⁿ pages par feuille.

Musique

La gamme du tempérament égal se construit ainsi : le rapport de fréquences entre les notes extrêmes de l'octave est 2 ; et la gamme est divisée en douze-demi tons de rapports de fréquence égaux f. Le rapport de fréquences entre la note la plus haute et la plus basse est donc f¹², qui vaut, comme indiqué précédemment, 2. Le demi-ton a ainsi un rapport f = 2^1/12.

Rapports de fréquences des notes de la gamme tempérée par rapport à la note la plus basse.

do

do#

ré

ré#

mi

fa

fa#

sol

sol#

la

la#

si

do

1

21/12

21/6

21/4

21/3

25/12

√2

27/12

22/3

23/4

25/6

211/12

2

Dans ce système, la quarte augmentée (do–fa#) et la quinte diminuée (do-sol♭) sont égales et valent six demi-tons ; elles ont un rapport de fréquences de √2. Le chant grégorien utilise cet intervalle, le triton, mais à la fin du Moyen Âge celui-ci est systématiquement évité car jugé trop dissonant. Il reçoit alors le surnom de « Diabolus in Musica ».

Électricité

En électricité, la tension efficace U_eff d'un courant alternatif sinusoïdal — par exemple les 110 V ou 220 V du courant domestique — est reliée à l'amplitude de la tension U_max par

U_max = U_eff√2, noté aussi Û=U√2,

soit, dans la plupart des applications courantes :

U_eff ≅ 0,7 U_max.

Cela est valable plus généralement pour la valeur efficace des grandeurs linéaires d'une onde sinusoïdale.

Photographie

Les ouvertures des appareils photographiques suivent la séquence normalisée f/1,4, f/2 f/2,8 f/4 f/5,6 f/8 f/11 f/16 f/22, f/32, etc. Le rapport entre deux ouvertures consécutives est une valeur proche de √2, qui a été choisie de sorte à ce que le rapport de flux lumineux soit dans un rapport 2 (flux = diamètre²). En diminuant d'un « cran » l'ouverture on double le temps de pose nécessaire ou diminue d'un facteur 2 la sensibilité de la pellicule requise.^[2]

Dans la pratique, l'ouverture indiquée est un arrondi ; l'ouverture réelle peut coller au plus proche de ^[3]. Il existe des subdivisions sur les appareils modernes, souvent dans des rapports 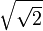ou .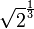

Lien entre ouverture, diamètre du diaphragme et flux lumineux reçu à pose et sensibilités fixés.

Ouverture	f/1,4	f/2	f/2,8	f/4	f/5,6	f/8	f/11	f/16	f/22	f/32
Diamètre	d	d/√2	d/2	d/2√2	d/4	d/4√2	d/8	d/8√2	d/16	d/16√2
Flux	I	I/2	I/4	I/8	I/16	I/32	I/64	I/128	I/256	I/512

Histoire

Babylone

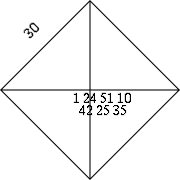
La première représentation connue de ce nombre date du début du II^e millénaire av. J.-C.. Il apparaît sur la tablette babylonienne YBC 7289 datant de -1700 ± 100. Il s'agit du tracé d'un carré avec ses diagonales, avec les mesures des segments et accompagné d'une valeur approchée de √2 écrite en système sexagésimal cunéiforme :

      ,

ce qui signifie très probablement 1 + 24/60 + 51/60² + 10/60³ — l'absence de zéro et de virgule dans la numération babylonienne rend la notation positionnelle ambiguë — soit environ 1,41421296. Il s'agit d'une valeur approchée au six dix-millionièmes de , ce qui indique qu'elle avait été obtenue de manière algorithmique, car une telle précision de mesure leur était hors de portée.

On sait d'ailleurs que les Babyloniens savaient extraire des racines carrées d'entiers non carrés en exploitant des formules du type de la méthode de Héron^[4] (ces formules sont un cas particulier de la méthode de Newton).

Grèce antique

Les pythagoriciens attribuèrent une grande importance à la notion de grandeurs commensurables et s'y tinrent longtemps comme à un principe philosophique. Ils ne pouvaient concevoir qu'un nombre ne soit pas un rapport d'entiers, le rapportant le plus souvent à des figures géométriques. Mais d'après Aristote (IV^e siècle av. J.-C.), ce sont les pythagoriciens eux-mêmes qui démontrèrent pour la première fois que est irrationnel, à la fin du V^e siècle av. J.-C., à savoir qu'il ne peut s'écrire comme le rapport de deux grandeurs commensurables. Cette démonstration de l'incommensurabilité de , supposée pour une grande part géométrique, est souvent attribuée à Pythagore, mais elle aurait en fait été rédigée par l'un de ses disciples. Une légende rapporte que, parce que contraire aux pensées de Pythagore sur le caractère absolu des nombres, la découverte d'un nombre irrationnel jeta un trouble au sein de l'école et la démonstration fut dissimulée. Une autre légende mise en doute par Proclus raconte qu'Hippase de Métaponte fut jeté à la mer et mourut noyé pour avoir révélé l'existence de cette démonstration. Beaucoup de doutes subsistent sur ces récits. D'ailleurs certains émettent l'hypothèse qu'il ne s'agissait pas de mais plutôt du nombre d'or 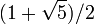. Platon rapporte dans son Théétète, que Théodore utilisait une méthode générale pour démontrer l'incommensurabilité à un des racines carrées de 3, 5… 17 mais sans nous la révéler. Ainsi l'incommensurabilité de à 1, pourrait bien avoir tout de même été établie par les pythagoriciens. La plus ancienne preuve de l'incommensurabilité de 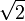avec 1 qui ait traversé le temps, figure dans les textes d'Aristote (Aristote, Analytiques Postérieurs I), qui affirme que si la diagonale du carré était commensurable avec le côté, alors un même nombre serait pair et impair. Une autre démonstration se trouve dans le livre 10 des Éléments d'Euclide et repose sur la méthode d'anthyphérèse, aussi appelée méthode de soustraction réciproque.

On suppose que l'algorithme de Théon de Smyrne, inspiré de la méthode d'antiphérèse, aurait été utilisé à l'époque pour calculer des valeurs approchées de . Il permet, en considérant les rapports de termes des deux suites introduites par Théon et en utilisant le principe de l'encadrement, d'obtenir des valeurs approchées de comme 3/2, 7/5, ou 17/12.

Précisons qu'il faudra attendre Diophante pour que et les autres irrationnels, ainsi que les rationnels soient considérés comme des nombres à part entière, algébriquement parlant.

Monde indien

On peut trouver dans le Śulbasutra de Baudhayana une approximation de 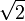antérieure au V^e siècle av. J.-C.^[5].

Monde musulman

Le monde Musulman connaissait l'irrationalité √2, au moins par traduction des textes grecs. Les travaux de Muhammad ibn Musa al-Khwarizmi (un mathématicien persan) introduisent la notation algébrique la généralise les problèmes et équations du second ordre^[6]. Un de ses successeurs, Abu Kamil systématise la manipulation des irrationnels. Ces deux mathématiciens développent et perfectionnent les algorithmes d'approximation des irrationnels, dont √2.

Occident

Géométrie

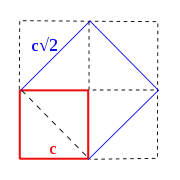
Quelques constructions classiques de √2.

1. Le théorème de Pythagore énonce que dans un triangle ABC rectangle en C, AB²=AC²+BC². Si ce triangle est un carré coupé en diagonale, la mesure de ses côtés peut être ramenée à l'unité, AC=BC=1, d'où AB²=1+1=2. Par conséquent AB=√2.
2. Dans un carré, la diagonale est multiple de √2 par rapport aux côtés.
3. On peut construire un carré de surface 2. L'aire d'un carré est égale au produit de ses côtés (c × c = c²). La racine de sa surface du carré est son côté et par construction, celui-ci est égal à √2. c² = 2 donne c = √2 ~ 1,4142. Cette construction est à l'origine de l'expression racine carrée.
4. La duplication du carré est une construction géométrique qui vérifie l'existence du nombre √2.

Duplication du carré

intervient dans la duplication du carré. C’est-à-dire la résolution du problème :

Un carré étant donné, comment construire un carré dont la surface est double ?

Ce problème, dont la résolution géométrique est relativement simple, offre un double intérêt historique : d'une part, il a servi de base à une démarche pédagogique célèbre racontée dans le Ménon de Platon (vers 400 av. J.-C.). D'autre part, il a poussé les mathématiciens à s'intéresser à un problème qui semblait similaire mais qui se révéla insoluble dans le cadre de la construction à la règle et au compas : la duplication du cube.

Dans le Ménon de Platon, Socrate cherche à prouver à Ménon que la vertu ne s'enseigne pas mais est intrinsèque. Il pose à un esclave le problème de la duplication du carré et va l'amener à trouver « seul » la solution du problème. La démarche de l'esclave suit une voie assez classique. Il propose de multiplier le côté par deux. Socrate l'amène à trouver qu'alors l'aire est multipliée par 4. L'esclave propose ensuite de considérer un carré dont le côté est la moyenne arithmétique du côté initial et de son double. Socrate l'amène à trouver que l'aire vaut alors les 9/4 de l'aire initiale. L'esclave arrive à une impasse : il ne peut trouver un nombre solution du problème. Socrate le guide alors vers la voie géométrique, il reproduit 3 carrés semblables au premier et trace une diagonale. L'esclave poursuit le raisonnement et construit enfin la solution au problème. D'après Socrate, l'esclave a retrouvé en lui une vérité qu'il possédait ; la démarche employée ressortit à la maïeutique.

On peut donc affirmer :

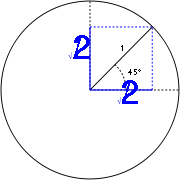
Le rapport entre le côté et la diagonale d'un carré est

Autrement dit, si d est la longueur de la diagonale et c celle du côté

Triangle rectangle isocèle

Dans un triangle rectangle, si les deux côtés adjacents à l'angle droit ont une longueur égale à l'unité, l'hypoténuse a pour longueur de √2. Ce résultat est un cas particulier du théorème de Pythagore.

La théorème de Pythagore affirme en effet que dans un triangle rectangle, le carré de l'hypoténuse — côté opposé à l'angle droit — est égal à la somme des carrés des côtés adjacents à l'angle droit. Sur la figure ci-contre, cela se traduit par

a² + b² = c²

Sur le triangle ci-contre cela donne ainsi

1² + 1² = c².

Cela veut dire que le carré de l'hypoténuse c² vaut 2. On en déduit que l'hypoténuse elle-même est de longueur

.

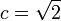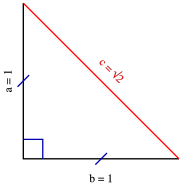
Trigonométrie

La moitié de √2 est une quantité commune en géométrie et en trigonométrie, car le vecteur unitaire qui fait un angle de 45° avec l'axe des abscisses, dans un repère orthonormé, a pour coordonnées :

Ce nombre satisfait cette relation :

√2/2 = 1/√2 = cos 45° = sin 45°

Construction de √2 à la règle et au compas

Comme toutes les racines carrées de nombre entier, est constructible à la règle et au compas ; a contrario, ce n'est pas le cas de la racine cubique de 2, par exemple.

Étant donné un segment AB de longueur unité, voici les différentes étapes pour construire un segment de longueur avec une règle non graduée et un compas :

1. Tracer le symétrique B' de B par rapport à A
   • Tracer le cercle C₁ de centre A et de rayon AB, il coupe la demi-droite ]BA) en B'
2. Tracer la médiatrice (AH) de [BB']
   • Tracer le cercle C₂ de centre B et de rayon r > AB
   • Tracer le cercle C₃ de centre B' et de rayon r, il coupe C₂ en deux points, H et H'
   • Tracer le segment [AH] il intersecte C₁ en un point C.

À cette étape le segment [BC] de longueur est construit.

Construction de √2 au compas seul

Comme tout nombre constructible à la règle et au compas, est constructible au compas seul. Les étapes d'une construction possible sont :

1. Tracer quatre sommets consécutifs B, G, H, I de l'hexagone régulier de centre A et de sommet B ; ceci permet de construire √3, l'unité étant la longueur AB.
   • Tracer le cercle C₁ de centre A et de rayon AB ;
   • Tracer le cercle C₂ de centre B et de rayon AB, il coupe C₁ en deux points, soit G l'un d'entre eux ;
   • Tracer le cercle C₃ de centre G et de rayon AB, il coupe C₁ en B et H ;
   • Tracer le cercle C₄ de centre H et de rayon AB, il coupe C₁ en G et I ;
2. Construire un triangle rectangle ABC d'hypoténuse AC = √3 (AB = 1) ; C est l'un des deux points tel que IC = IG et BC = BH (sachant que IG = BH = √3 > IB/2 = 1).
   • Tracer le cercle C₅ de centre I et de rayon IG ;
   • Tracer le cercle C₆ de centre B et de rayon BH (= IG), il coupe C₅ en C.

À cette étape le segment [AC] de longueur est construit.

Éléments de démonstration : IC = IG = √3, car d'après le théorème de Pythagore, les hauteurs en I et G des triangles équilatéraux de côté 1, IHA et HAG, qui sont portées par la médiatrice de (H, A), ont pour longueur √3/2. Par construction (A et C sur la médiatrice de BI) (AC) est perpendiculaire à (AI) et le théorème de Pythagore dans IAC donne AC² = 2..

Propriétés mathématiques principales

Irrationalité

est un nombre irrationnel : il n'est pas possible de l'écrire 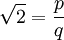, c'est-à-dire sous la forme d'une fraction de deux nombres entiers p et q.

Anciennement, on parlait d'incommensurabilité de 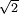et 1 : il n'existe pas d'unité u permettant de mesurer à la fois le côté d'un carré et sa diagonale ; ce qui se traduit mathématiquement par la proposition suivante : il n'existe pas p et q entiers tels que :

.

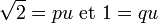Ces deux formulations sont équivalentes.

Il existe de multiples démonstrations de l'irrationalité ; de par leur simplicité elles sont souvent utilisées à des fins pédagogiques comme introduction à la théorie des nombres. Elles procèdent le plus souvent par l'absurde. L'incohérence typique est l'existence d'une descente infinie d'entiers naturels ou la simplification d'une fraction irréductible. La forme de la preuve peut utiliser des arguments purement arithmétiques ou utiliser une représentation géométrique.

Démonstration géométrique

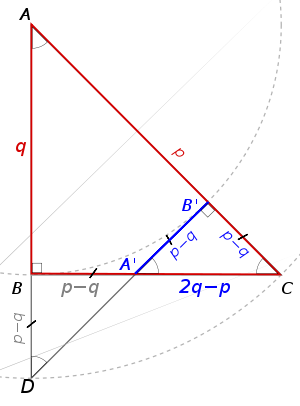
La démonstration qui suit est une variante particulièrement simple de la démonstration géométrique des anciens grecs^[7]. Elle fournit quasiment une évidence géométrique de l'irrationalité de √2 : étant donné un triangle isocèle rectangle dont l'hypoténuse a pour longueur un multiple entier de la longueur des deux autres côtés, on peut alors construire un triangle isocèle rectangle de dimensions strictement inférieures ayant la même propriété, ce qui montre par descente infinie qu'un tel triangle ne peut exister.

En effet supposons 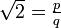avec p et q entiers. Soit alors un triangle ABC rectangle isocèle en B de côté BA = BC = q, son hypoténuse est ainsi AC = BA × √2= p.

Le cercle de centre A et de rayon AB intersecte l'hypoténuse [AC] en B'. Le cercle de centre A et de rayon AC intersecte le côté [AB) en D. Le point A' est à l'intersection des droites (BC) et (B'D).

• Les triangles ABC et AB'D, ayant un angle commun et deux côtés deux à deux de même longueur, sont isométriques. L'angle 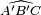est donc droit. Comme 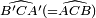est un demi-angle droit, A'B'C est isocèle rectangle en B'. Pour des raisons analogues A'BD est isocèle rectangle en B.
• Les longueurs des côtés de ces deux triangles, sont entières, en effet :
  • B'C = AC - AB = p - q,
  • BD = AC - AB = p - q,
  • BA' = BD = p - q (car A'BD est isocèle rectangle en B).
  • A'C = BC - BA' = q - (p - q) = 2q - p.

Le triangle A'B'C est rectangle isocèle en B' de côté p - q et d'hypoténuse 2q - p, tous les deux entiers.

En continuant ainsi, on obtient une descente infinie de triangles à côtés entiers ABC, A'B'C, etc. ce qui est absurde.

On a bien montré que 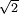ne peut pas s'écrire 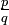avec p et q entiers.

Démonstration arithmétique

On suppose par l'absurde que la racine carrée de 2 est rationnelle. Dans ce cas on pourrait écrire √2 sous forme de fraction irréductible, c'est-à-dire que p et q n'auraient pas de facteurs premiers communs. Il en serait donc de même pour p² et q², ce qui signifierait que p²/q² serait une fraction sous sa forme irréductible. Une telle forme étant unique, l'égalité p²/q² = 2/1 entraînerait p² = 2 et q² = 1. La première de ces deux égalités est impossible pour p entier ; on a donc abouti à une contradiction.

Il existe différentes variantes de cette preuve. Sous cette forme, elle demande quelques connaissances arithmétiques, en particulier le lemme de Gauss (ou lemme d'Euclide) pour l'unicité de la forme irréductible d'une fraction. Elle se généralise directement pour montrer l'irrationalité de la racine carrée d'un entier qui n'est pas un carré parfait.

Si on s'intéresse seulement à l'irrationalité de √2, on peut en ramener l'argumentation à des considérations élémentaires de parité comme suit : si √2 était rationnel, il pourrait s'écrire sous forme d'une fraction p/q telle qu'au moins l'un des deux entiers p et q soit impair. Il suffit de simplifier par 2 jusqu’à que ce ne soit plus possible (argument de descente infinie). On remarque que le carré d'un nombre impair, c'est-à-dire de la forme 2k+1, est impair : (2k+1)² = 2(2k² + 2k)+1. Comme tout nombre est pair (de la forme 2k) ou impair, on en déduit que, si le carré d'un nombre est pair, ce nombre ne peut être que pair. L'identité p² = 2q² impliquerait que p² et donc aussi p seraient pairs. Il s'en suivrait que p² serait divisible par 4, donc q² par 2. À nouveau q² et donc q seraient pairs. Mais p et q seraient tous les deux pairs, d'où contradiction.

Ces deux démonstrations se trouvent dans le livre X des Éléments d'Euclide. La deuxième est très ancienne car Aristote y fait allusion, comme un fait bien connu.

Normalité

La normalité est un concept se basant sur la distribution des chiffres du développement décimal d'un nombre irrationnel, à savoir si tous les chiffres de 0 à 9 apparaissent dans ce développement et avec la même fréquence. En ce qui concerne √2, on ignore s'il est normal dans le système décimal ou dans toute autre base de numération.

Degré algébrique et degré d'irrationalité

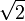est un nombre algébrique de degré 2, dit entier quadratique, car solution de l'équation polynômiale du second degré à coefficients entiers x² − 2 = 0 et de monôme dominant de coefficient égal à un, mais d'aucune de degré 1 de par son irrationalité. On sait ainsi qu'il est difficilement approchable par une suite rationnelle p_n/q_n ; l'erreur est en mieux en

|√2 − p_n/q_n| ~ 1/q_n².

Comme pour tout nombre algébrique irrationnel, son degré d'irrationalité est 2.

Proportion d'argent

La proportion d'argent est une constante mathématique obtenue à partir de  :

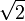Elle peut aussi être écrite comme une fraction continue :

δ_Ag = [2; 2, 2, 2, …]

On peut écrire les puissances de la proportion d'argent ainsi :

où la suite (u_n) est définie par récurrence :

Note : il y a une ressemblance avec les propriétés de la proportion dorée, dont les puissances successives s'expriment en fonction de φ et 1/φ et d'une suite récurrente double.

Développement en fraction continue

√2 est relié à un certain nombre de développements en fractions continues périodiques, par propriété des entiers quadratiques.

√2 est relié au développement en fraction continue suivant

pour 2a² − b² = 1, (a, b) entiers strictement positifs. On notera ce développement de manière plus concise :

a√2 − b = [0; 2b, 2b, 2b, …]

On en tire les valeurs suivantes de √2 :

√2 = [1; 2, 2, 2, …].

√2 = 1/5 × [7; 14, 14, 14, …]

√2 = 1/29 × [41; 82, 82, 82, …]

Plus généralement, se relie à la fraction continue généralisée suivante :

notée sous forme plus concise

a√2 − b = [0; k, 2b; k, 2b; k, 2b; …]

avec k = 2a² − b², et (a, b) entiers strictement positifs. On en déduit les quelques développements de 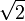suivants :

√2 = 1/2 × [3; -1, 6; -1, 6; -1, 6; …]

√2 = 1/12 × [17; -1, 34; -1, 34, -1, 34; …]

√2 = 1/70 × [90; -1, 180; -1, 180, -1, 180; …]

Éléments de démonstration : soit la suite (u_n) définie par la relation de récurrence u_{n + 1} = −k/(2b + u_n) et ε_n = |u_n − (a√2 − b)|. Alors on peut montrer que ε_{n + 1} < Kε_n, avec 1/|1 + 2b/(a√2 − b)| < K < 1 dans un voisinage de a√2 − b.

Développements en série et produit infini

Produits infinis

L'identité cos(π/4) = sin(π/4) = 1/√2 et la représentation en produit infini du sinus et du cosinus mènent aux développements suivants

Le dernier produit peut s'écrire de manière équivalente :

Séries

Le nombre peut aussi être évalué sous forme de série par le développement de Taylor d'une fonction trigonométrique en  :

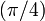On peut aussi utiliser la fonction 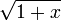en 1:

La convergence de la dernière série peut être accélérée par le biais d'une transformation d'Euler pour donner :

Méthodes numériques d'approximation

√2 vaut approximativement 1,414 213 562 373 095 048 801 688 724 209 698 078 569 671 875 376 948 073 176 679 737 990 732 478 462 107 038 850 387 534 327 641 572 7

Le calcul d'une valeur approchante de √2 a été un problème mathématique pendant des siècles. Ces recherches ont permis de perfectionner les algorithmes de calculs d'extraction de racines carrées. En informatique, ces recherches se sont poursuivies afin d'optimiser ces algorithmes en réduisant les temps de calcul et la consommation de mémoire^[8].

Les méthodes numériques d'approximation présentées ci-dessous sont destinées au calcul d'un nombre important de décimales. Elles se basent généralement sur une suite convergente de nombres rationnels ; ainsi l'itération s'affranchit du coût de calcul sur des nombres à virgule flottante — dont il faudrait en plus connaître la précision a priori. Les meilleures approximations par une suite rationnelle p_n/q_n donnent une erreur en 1/q_n², une propriété de l'approximation diophantienne des entiers quadratiques.

Méthodes à convergence linéaire

Méthode de Théon de Smyrne

On doit à Théon de Smyrne ces deux suites (p_n) et (q_n) définies par récurrence :

p_{n + 1} = p_n + 2q_n,     p₀ = 1 ;

q_{n + 1} = p_n + q_n,     q₀ = 1.

Ces suites sont à valeur entière strictement positive, donc strictement croissantes par récurrence, et vérifient

p_n² − 2q_n² = (−1)ⁿ(p₀² − 2q₀²)

de sorte que p_n/q_n tend vers √2.

On ne sait pas si l'intention de Théon de Smyrne était de calculer une valeur approchée de √2.

Solutions de l'équation diophantienne a²− 2b² = k

Les solutions entières de l'équation a² − 2b² = k sont générées par récurrence

a_{m + 1} = 3a_m + 4b_m

b_{m + 1} = 2a_m + 3b_m

à partir des valeurs initiales (a₀, b₀) = (1, 1) pour k = −1 et (3, 2) pour k = 1.

Cette méthode est déduite de celle de Théon : chaque itération de la présente correspond à deux itérations de celle-là. Ainsi, a_n/b_n tend linéairement vers √2.

Les premières solutions sont :

• k = −1 :  (1, 1),  (7, 5),  (41, 29),  (239, 169),  (1393,985),
• k =   1 :  (3, 2),  (17, 12),  (99, 70),  (577, 408),  (3363, 2378).

Les deux approximations mises en gras furent utilisées en pratique par les arpenteurs anciens :

• 28 : 20  avec l'erreur relative de – 1,0051 %, brièvement au début du III^e millénaire av. J.-C. par les Égyptiens Anciens (cf. le remen de construction) et
• 99 : 70  avec l'erreur relative de + 0,0051 %, tout au long de l'histoire et dans beaucoup de pays dans la triangulation rationnelle du carré selon les arpenteurs.

Méthode de Théon généralisée

On se donne (a, b), obtenues par la méthode de Théon, qui sont donc solutions de l'une des deux équations diophantiennes précédente 2b² = a² - k = K, avec k = ±1 et K> 1. On peut alors écrire

√2 = a/b √[K/(K + k)]

Les suites p_n et q_n définies par

p_{n + 1} = (2K + k)p_n + 2Kq_n,     p₀ = 1 ;

q_{n + 1} = (2K + 2k)p_n + (2K + k)q_n,     q₀ = 1.

vérifient

(K + k)p_{n + 1}² - K q_{n + 1}² = (K + k)p_n² - K q_n² = … = k,

et donc, de la même façon que ci-dessus, la suite p_n/q_n converge vers √[K/(K + k)]. De plus, si k = 1, cette suite est croissante donc approche cette valeur par défaut, et si k = -1, elle est décroissante donc approche cette valeur par excès.

On peut utiliser cette relation pour estimer l'erreur :

ε_{n + 1} ≈ ε_n (4K + 3k)⁻²

et c'est une majoration si k= 1. La convergence est donc linéaire : elle fait gagner un nombre à peu près constant de décimales à chaque itération.

Cette méthode correspond à une généralisation de la méthode du paragraphe précédent au radical √[K/(K + k)]. Pour K plus grand, la suite q_n croit plus rapidement, donc la convergence est accélérée.

Premières approximations de √2 = 17/12 √(288/289) par approximation linéaire de √(288/289). Les paramètres sont a = 17, b = 12, K = 288, k = 1. On a
ε_{n + 1} < 7,5 × 10^-7ε_n   (avant approximation décimale des quotients).

itération	valeur fractionnaire	décimales exactes
0	1	1
1	19601/13860	1,41421356
2	22619537/15994428	1,41421356237309
3	26102926097/18457556052	1,41421356237309504880
4	30122754096401/21300003689580	1,41421356237309504880168872

Développement en fraction continue

Une autre méthode consiste à approcher a√2 − b par sa fraction continue généralisée pour (a, b) solutions de l'équation diophantienne 2a² = b² + k, avec k = ± 1 :

a√2 − b = [0; k, 2b; k, 2b; k, 2k, …].

m√2 − n est approximé à l'aide de la suite (p_n/q_n) déterminée par la relation de récurrence

p_{n + 1} = q_n

q_{n + 1} = 2bq_n + kp_n

L'erreur vérifie asymptotiquement

ε_{n + 1} < |a√2 − b|/(2b − 1) ε_n

Premières approximations de √2 par approximation linéaire de 169√2 − 239. Les paramètres sont a = 169, b = 239, k = 1, ε_{n + 1} ~ 4 × 10⁻⁶ ε_n.

itération	valeur fractionnaire	décimales exactes
0	1	1
1	114243/80782	1,414213562
2	54608393/38613965	1,41421356237309
3	26102926097/18457556052	1,41421356237309504880
4	12477253282759/8822750406821	1,4142135623730950488016887

Développement de Taylor

On se donne (a, b) solutions de l'équation diophantienne 2a² = b² + k = K, avec k = ±1. On peut alors écrire le développement de Taylor de √[K/(K − k)]

et utiliser √2 = b/a √[K/(K − k)]

Dans le cas √2 = 7/5 √(50/49), ce développement se simplifie de façon remarquable comme l'a fait remarquer Leonhard Euler en 1755 :

Approximation √2 = 239/169 √(57122/57121) par le développement de Taylor du radical fractionnaire. Les paramètres sont a = 239, b = 169, K = 57122, k = 1.

itération	valeur fractionnaire	décimales exactes
0	1	1
1	239/169	1,4142
2	6238763163557/4411471739168	1.41421356237309
3	712741258857407103/503984177369508992	1.414213562373095048
4	325705649507622468308893/230308673437608741128192	1.414213562373095048801688

Dichotomie

Il est possible d'approcher √2 par bissection. Cette méthode est de convergence linéaire lente : on gagne trois décimales à chaque dizaine d'itérations.

Méthode à convergence quadratique

La méthode de Newton appliquée à la fonction racine carrée permet de calculer une valeur approchée de √2 de manière itérative avec une convergence quadratique, c'est-à-dire doublant le nombre de décimales à chaque itération. La récurrence a la forme

u_{n + 1} = u_n/2 + 1/u_n

Cet algorithme s'appelle méthode de Héron ou méthode babylonienne car il semble que ce soit celle utilisée par les babyloniens pour trouver des valeurs approchées de racines carrées.

Si l'on s'intéresse aux fractions successives à partir d'une valeur initiale p₀ et q₀, la récurrence sur le numérateur et le dénominateur sont

p_{n + 1} = p_n² + 2q_n²

q_{n + 1} = 2p_nq_n

Premières approximations de √2 données par la méthode de Newton.

itération	valeur fractionnaire	décimales exactes
0	1	1
1	3/2	1
2	17/12	1,41
3	577/408	1,41421
4	665857/470832	1,41421356237
5	886731088897/627013566048	1,41421356237309504880168

Méthodes cubiques

Méthode de Halley

Un exemple de méthode cubique s'obtient par l'itération de Halley. Elle cherche le zéro de f(x) = x² − 2 en utilisant les deux premières dérivées. La solution itérative est

x_{n + 1} = x_n × (x_n² + 6)/(3x_n² + 2)

soit en posant x_n = p_n/q_n :

p_{n + 1} = p_n(p_n² + 6q_n²)

q_{n + 1} = q_n(3p_n² + 2q_n²)

Cette méthode est de convergence cubique : le nombre de décimales exactes triple à chaque itération.

Premières approximations de √2 données par la méthode cubique.

itération	valeur fractionnaire	décimales exactes
0	1	1
1	7/5	1,4
2	1393/985	1,414213
3	10812186007/7645370045	1,414213562373095048
4	—	1,4142135623730950488 016887242096980785696 718753769480731766797

Méthode de Householder

L'itération de Householder appliquée à f(x) = 1/x² − 1/√2 donne une suite convergeant vers 1/√2 :

x_{n + 1} = x_n + x_n/8 × (2x_n² − 1)(6x_n² − 7)

Méthodes d'ordre supérieur

On utilise une méthode de Newton modifiée^[9] pour trouver le zéro de f(x) = 1/x² − 1/2. Cela donne la suite récurrente :

x_{n + 1} = x_n + x_n/16 × (8h_n + 6h_n² + 5h_n³)

avec

h_n = 1 − x_n²/2

Cette méthode est de convergence quartique, i.e. d'ordre 4 : le nombre de décimales exactes quadruple à chaque itération.

Premières approximations de √2 données par la méthode quartique.

itération	valeur fractionnaire	décimales exactes
0	3/2	1
1	23169/214	1,414
2	57367317478181003155381859082363/2105	1,41421356237309
3	—	1,41421356237309 5048801688724209 6980785696718753 76948073176679737

Il existe des méthodes d'ordre supérieur^[10], notamment parmi les méthodes de Householder.

Notes et références

Bibliographie

• Benoît Rittaud, Le Fabuleux Destin de √2, Le Pommier, 2006, (ISBN 2746502755)
• Nicolas Bourbaki, Éléments d'histoire des mathématiques, Hermann, 1974, (ISBN 978-2705657789)
• Bertrand Hauchecorne et Daniel Suratteau, Des mathématiciens de A à Z, Ellipses, (ISBN 978-2729846831)
• Denis Daumas, « Sur la démonstration de l'irrationalité chez les grecs », in La démonstration mathématique dans l'histoire, IREM de Lyon
• (en) David Henderson Square Roots in the Sulbasutra, Geometry at Work: Papers in Applied Geometry (editor, C. A. Gorini), MAA Notes Number 53, pp. 39-45, 2000, en ligne sur le site de l'auteur
• (en) Eleanor Robson & David Fowler, « Square root approximations in Old Babylonian mathematics : YBC 7289 in context », Historia Mathematica, 25, pp. 366-378, 1998 [lire en ligne] [pdf]

Voir aussi

Articles connexes

• Racine carrée
• Livre X des Éléments d'Euclide
• Nombre irrationnel
• Nombre algébrique

Liens externes

• (fr) Racine de 2, Benoît Rittaud (ressources en ligne autour du livre Le Fabuleux Destin de √2, consulté le 24 août 2006)
• (en) Square root of 2 is irrational, Alexander Bogomolny (9 démonstrations de l'irrationalité de √2, consulté le 23 août 2006)
• (en) Pythagoras' Constant √2, Xavier Goudon et Pierre Sebah (diverses approximations rationnelles de 2, visité le 23 août 2006)
• (en) Pythagoras's Constant on Math World (consulté le 23 août 2006)
• Ludmila Duchêne et Agnès Leblanc, Exercice de styles (démonstrations de l'irrationalité de racine de 2), 2009 [lire en ligne] [pdf]

Notion de nombre
Ensembles usuels	Entier naturel • Entier relatif • Nombre décimal • Nombre rationnel • Nombre réel • Nombre complexe
Extensions	Quaternion • Octonion • Sédénion • Nombre complexe fendu • Tessarine • Nombre bicomplexe • Nombre multicomplexe • Biquaternion • Coquaternion • Octonion fendu • Nombre hypercomplexe • Nombre p-adique • Nombre hyperréel • Nombre superréel • Nombre dual • Droite réelle achevée • Nombre cardinal • Nombre ordinal • Nombre surréel et pseudo-réel
Propriétés particulières	Parité • Nombre premier • Nombre composé • Carré parfait • Nombre parfait • Nombre positif • Nombre négatif • Fraction dyadique • Nombre irrationnel • Nombre algébrique • Nombre transcendant • Nombre imaginaire pur • Nombre de Liouville • Nombre normal • Nombre univers • Nombre constructible • Nombre réel calculable • Nombre transfini • Infiniment petit • Infiniment grand
Exemples d’importance historique	π Pi • √2 Racine carrée de deux • φ Nombre d’or • 0 Zéro • i Unité imaginaire • e Constante de Neper • ℵ0 Aleph-zéro • Table de constantes mathématiques
Notions connexes	Chiffre • Numération • Fraction • Opération • Calcul • Algèbre • Arithmétique • Suite d’entiers • ∞ Infini • Chiffre significatif

• Portail des mathématiques
• Portail de la géométrie

La version du 19 avril 2007 de cet article a été reconnue comme « bon article » (comparer avec la version actuelle). Pour toute information complémentaire, consulter sa page de discussion et le vote l’ayant promu. La version du 19 avril 2007 de cet article a été reconnue comme « bon article », c'est-à-dire qu'elle répond à des critères de qualité concernant le style, la clarté, la pertinence, la citation des sources et l'illustration.