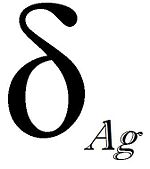- Proportion d'argent
-
La proportion d'argent est une constante mathématique obtenue à partir de la racine carrée de deux et est aussi un nombre irrationnel. Ce nom fait référence à la proportion dorée.
Sommaire
Définition
La proportion d'argent, notée δAg, vaut
. Dès lors, 
Elle peut aussi être écrite comme une fraction continue [2, 2, 2, 2,…]::
Propriétés
En approximation diophantienne, la suite des parties fractionnaires des :
- xn, pour
est équidistribuée modulo un, pour presque tous les nombres réels x > 1. La proportion d'argent est une exception.
Les puissances les plus basses de la proportion d'argent sont:
Les puissances se succèdent en suivant le modèle:
où
- Kn = 2K(n − 1) + K(n − 2)
Par exemple, en utilisant cette relation:
En utilisant K0 = 1 et K1 = 2 comme conditions initiales, une formule analogue à celle de Binet se déduit de la résolution de la récurrence
- Kn = 2K(n − 1) + K(n − 2)
ce qui donne
Les moyennes d'argent
Les fractions continuées plus générales
![[n,n,n,\dots]=\frac{1}{2}\left(n+\sqrt{n^2+4}\right)](8/c9824ba8041a1b5bd31a67eaf5cd501a.png)
sont appelées les moyennes d'argent[1]. La proportion d'or correspond à la moyenne d'argent pour n = 1, tandis que la proportion d'argent est la moyenne d'argent pour n = 2. Une table contenant les valeurs des cinq premières moyennes d'argent peut être trouvée en référence[2].La propriété ci-dessus pour les puissances de la proportion d'argent peut-être considérée comme une conséquence d'une propriété des puissances des moyennes d'argent.
Pour une moyenne d'argent Ag de m notée Agm (
![Ag_m=[n,n,n,\dots]](e/fae45457c80e7a46eae8f123b8be484a.png)
), la propriété peut être généralisée comme suit :où
- Kn = mK(n − 1) + K(n − 2)
En utilisant les conditions initiales K0 = 1 et K1 = m, cette relation de récurrence devient:
La moyenne d'argent Ag de m possède aussi la propriété suivante
ce qui implique que l'inverse d'une moyenne d'argent a la même partie décimale que la moyenne d'argent correspondante.
Si nous décomposons la moyenne d'argent Ag de m telle que:
- Agm = a + b
où a est la partie entière de Agm et b la partie décimale de Agm, alors nous avons:
Parce que pour tout m supérieur à 0, la partie entière de Agm est égale à m et a = m. Pour m > 1, nous avons alors
Par conséquent la moyenne d'argent de m est une solution de l'équation :
- x2 − mx − 1 = 0
Il peut être aussi utile de noter que la moyenne d'argent Ag de − m est l'inverse de la moyenne d'argent Ag de m
Les rectangles d'argent
Un rectangle de proportion (rapport de la longueur par la largeur) égale à la proportion d'argent est parfois appelé rectangle d'argent par analogie avec les rectangles d'or.
De façon confuse, « rectangle d'argent » peut aussi désigner un rectangle de proportion
, aussi connu sous le nom de rectangle A4 en référence au format de papier A4 respectant la norme ISO 216.Tous les rectangles d'argent ont la propriété qu'en retirant consécutivement deux carrés d'eux-mêmes ils donnent un plus petit rectangle d'argent[3]. Plus précisément, en retirant le plus grand carré possible d'un rectangle d'argent nous obtenons un rectangle d'une autre sorte, puis en recommençant une fois de plus nous obtenons un rectangle d'argent donc de la même forme que l'original mais plus petit d'un facteur
.Références
Notes
- traduction de silver mean par un rédacteur.
- Silver Ratio -- from Wolfram MathWorld
- http://www.scipress.org/journals/forma/pdf/1904/19040293.pdf
Voir aussi
Wikimedia Foundation. 2010.
