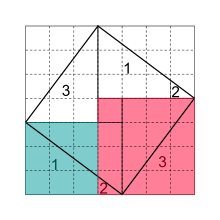
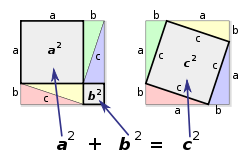
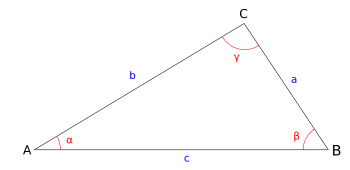
- Théorème de Pythagore
-
Le théorème de Pythagore est un théorème de géométrie euclidienne qui donne une formule reliant les longueurs des côtés dans un triangle rectangle : le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés.
Ce théorème permet notamment de calculer l’une de ces longueurs à partir des deux autres. Il est nommé d’après Pythagore de Samos, mathématicien, philosophe et astronome de la Grèce antique, même si le résultat a vraisemblablement été découvert indépendamment dans plusieurs autres cultures.
Les premières démonstrations historiques reposent en général sur des méthodes de calcul d’aire par découpage et déplacement de figures géométriques. Inversement, la conception moderne de la géométrie euclidienne est fondée sur une notion de distance qui est définie pour respecter ce théorème.
Divers autres énoncés généralisent le théorème à des triangles quelconques, à des figures de plus grande dimension telles que les tétraèdres, ou en géométrie non euclidienne comme à la surface d’une sphère.
Sommaire
Vocabulaire et énoncés
Un triangle rectangle est un triangle admettant un angle droit (c’est-à-dire de mesure 90°).
Les deux côtés adjacents sont appelés cathètes et le côté opposé est l’hypoténuse.
Théorème
La forme la plus connue du théorème de Pythagore est la suivante :
Théorème de Pythagore — Dans un triangle rectangle, le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des côtés de l’angle droit.
En particulier, la longueur de l’hypoténuse est donc toujours supérieure à celle de chaque autre côté.
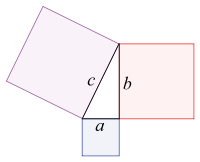
Le terme « longueur » est parfois omis, chaque côté étant assimilé à sa longueur. Toutefois l’élévation au carré (algébrique), qui n’a de sens que pour une grandeur numérique comme la longueur, correspond à la construction d’un carré (géométrique) sur chaque côté du triangle. Certaines démonstrations du théorème s’appuient d’ailleurs sur une égalité d’aires entre le carré construit sur l’hypoténuse et la réunion des carrés construits sur les deux autres côtés.
En nommant les sommets du triangle, le théorème peut se reformuler dans l’implication suivante :
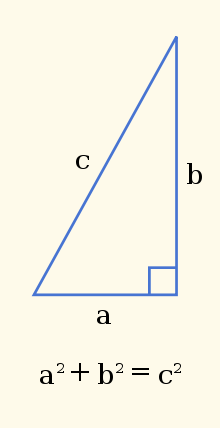
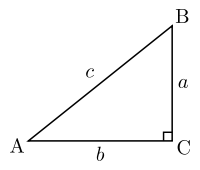
Théorème de Pythagore — Si un triangle ABC est rectangle en C, alors AB2 = AC2 + BC2.
Avec les notations usuelles AB = c, AC = b et BC = a (cf figure ci-dessous), la formule s’écrit encore : a2 + b2 = c2.
Par contraposée :
Théorème — Si AB2 n’est pas égal à AC2 + BC2 alors le triangle n’est pas rectangle en C.
Réciproque
L’implication réciproque est également vraie :
Réciproque du théorème de Pythagore — Si AB2 = AC2 + BC2 alors le triangle ABC est rectangle en C.
Pour une formulation sans notations des sommets, il faut éviter d’utiliser le terme « hypoténuse », qui n’est pas d’usage pour un triangle quelconque.
Réciproque du théorème de Pythagore — Si dans un triangle, le carré de la longueur du plus grand côté est égal à la somme des carrés des longueurs des deux autres côtés, alors ce triangle est rectangle et l’angle droit est l’angle opposé au plus grand côté, et le plus grand côté de ce triangle est son hypoténuse.
Par contraposée de la réciproque :
Théorème — Si un triangle ABC n’est pas rectangle en C, alors AB2 n’est pas égal à AC2 + BC2.
Applications
Arpentage
 Corde à treize nœuds disposée en triangle rectangle.
Corde à treize nœuds disposée en triangle rectangle.

 Vérification de la relation pour un triangle de longueurs de côté 3, 4 et 5.
Vérification de la relation pour un triangle de longueurs de côté 3, 4 et 5.D’après la réciproque du théorème de Pythagore, si un triangle a des côtés de longueurs 3, 4 et 5 (par rapport à une unité quelconque) alors il est rectangle.
Ce cas particulier de triplet pythagoricien justifie l’usage de la corde à treize nœuds, qui permettait de mesurer des distances mais aussi d’obtenir un angle droit sans équerre rigide en répartissant les douze intervalles qui séparent les nœuds sur les trois côtés d’un triangle de dimensions 3 - 4 - 5.
Nature d'un triangle
Le théorème (ou plutôt sa contraposée) et sa réciproque montrent que la relation donnée entre les longueurs des côtés est une propriété caractéristique des triangles rectangles, ce qui permet de l’utiliser comme test dans la détermination de la nature d’un triangle :
- si AB2 = AC2 + BC2 alors le triangle est rectangle en C ;
- si AB2 n’est pas égal à AC2 + BC2 alors le triangle n’est pas rectangle en C.
En procédant au test pour chacun des trois sommets du triangle, on obtient un algorithme qui détermine si le triangle est rectangle ou non à partir des longueurs de ses côtés.
Distance euclidienne
Dans le plan muni d’un repère orthonormé, la distance entre deux points s’exprime en fonction de leurs coordonnées cartésiennes à l’aide du théorème de Pythagore par :
Cette formule est analogue à celle qui donne la norme d’un vecteur de coordonnées (x;y) dans une base orthonormée :
Ces formules se généralisent en dimension plus grande.
Relation trigonométrique
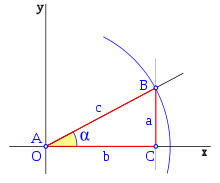
En considérant le cosinus et le sinus d’un angle α comme l'abscisse et l'ordonnée d’un point du cercle trigonométrique repéré par cet angle, le théorème de Pythagore permet d’écrire la relation suivante :
 Démonstration
DémonstrationHistoire
Origines
Les plus anciennes traces de la relation entre les longueurs des côtés d’un triangle rectangle peuvent être envisagées dans l’inscription de triplets pythagoriciens. Il s’agit de triplets d’entiers (a, b, c) satisfaisant la relation a2+b2=c2. Ils ont été relevés sur des tablettes babyloniennes, notamment la tablette Plimpton 322 datant du XVIIIe siècle av. J.‑C.), soit plus de 1 000 ans avant Pythagore. Certains prétendent même en trouver sur des mégalithes datant du XXVe siècle av. J.‑C. en Grande-Bretagne[1].
Parmi ces triplets, le plus petit d’entre eux est le triplet 3-4-5. Il correspond aux dimensions d’un triangle rectangle dont Plutarque conjecture une interprétation symbolique dès l’Égypte antique[2]. Ce triangle peut être formé à l’aide d’une corde à treize nœuds (voir plus haut) qui restera un outil des géomètres jusqu’à la fin du Moyen Âge[3].
Mais d’une part, l’utilisation de cette corde à nœuds n’indique pas forcément la connaissance du fait que l’angle formé est mathématiquement un angle droit ; d’autre part l’inventaire de triplets pythagoriciens a pu être entrepris dans un cadre arithmétique en dehors du contexte géométrique. Enfin, pour que le constat soit érigé en théorème, il faut que la relation soit démontrée, et pas seulement sur quelques cas particuliers.
Formulations
Le théorème, accompagné d’une démonstration, apparait au début du IIIe siècle av. J.‑C. dans les Éléments d’Euclide (proposition XLVII) sous la forme suivante[4] :
« Aux triangles rectangles, le carré du côté qui soutient l’angle droit, est égal aux carrés des deux autres côtés. »
Sa réciproque est la proposition XLVIII[4] :
« Si le carré de l’un des côtés d’un triangle est égal aux carrés des deux autres côtés, l’angle soutenu par ces côtés est droit. »
Les commentaires de Proclos (autour de l’an 400) semblent indiquer qu’Euclide n’aurait fait que retranscrire une démonstration plus ancienne que Proclos attribue à Pythagore. Cependant, les preuves historiques de la vie de Pythagore sont si rares qu’on ne peut lui attribuer avec certitude la paternité de cette démonstration.
Parallèlement au développement des mathématiques grecques, le théorème apparait en Chine dans le Zhoubi suanjing (« Le Gnomon des Zhou »), un des plus anciens ouvrages mathématiques chinois. Ce dernier, écrit probablement durant la dynastie Han (-206 à 220), regroupe des techniques de calcul datant de la dynastie Zhou (Xe siècle av. J.‑C. à -256). Le théorème ou procédure s’énonce de la manière suivante :
« En réunissant l’aire (mi) de la base (gou) et l’aire de la hauteur (gu) on engendre l’aire de l’hypoténuse. »
Mais la question se pose de savoir si ce théorème ou procédure est alors muni ou non d’une démonstration. Sur ce point les avis sont partagés(Chemla Shuchun, p. 681). Le théorème, sous le nom de Gougu (à partir des mots « base » et « altitude »), est repris dans le Jiuzhang suanshu (Les neuf chapitres sur l'art mathématique, -100 à 50), avec une démonstration, utilisant un découpage et une reconstitution, qui ne ressemble en rien à celle d’Euclide et qui prouve l’originalité de la démarche chinoise.
En Inde, vers -300, on trouve la trace d’une démonstration numérique de la propriété (preuve effectuée sur des nombres particuliers mais qui peut se généraliser aisément).
De nombreuses autres démonstrations ont été recensées depuis, utilisant des outils mathématiques variés. Léonard de Vinci et même le président américain James Garfield en ont proposé.
Conséquences
Le théorème de Pythagore pourrait avoir été à l’origine de la notions de grandeurs incommensurables, prémisse des nombres irrationnels. En effet, il montre[note 1] qu’un carré dont le côté sert d’unité a une diagonale dont le carré de la longueur vaut 2. Or aucune fraction d’entiers n’a de carré égal à 2. La construction géométrique d’un rapport « privé de raison » allait à l’encontre de la vision du monde de l’école pythagoricienne[5].
La recherche exhaustive des triplets pythagoriciens, motivée par la construction de triangles rectangles dont les longueurs de côté sont commensurables, s’est constituée en problème arithmétique à part entière. Elle ouvre la porte à la recherche de triplets satisfaisant une équation plus générale : an + bn = cn, où l’exposant n est un entier supérieur à 2. L’absence de solution lorsque l’exposant est supérieur ou égal à 3 est la conjecture de Fermat, qui n’a été définitivement démontrée que plus de trois siècles plus tard par Andrew Wiles.
Enfin, il a été démontré que le théorème de Pythagore est équivalent à l’axiome des parallèles[6].
Validation physique
Le théorème de Pythagore étant dérivé des axiomes de la géométrie euclidienne, sa validité dans le monde réel a pu être remise en question avec le caractère non euclidien de l’espace physique. Le mathématicien Carl Friedrich Gauss, ayant envisagé cette hypothèse près d’un siècle avant la naissance de la théorie de la relativité générale, aurait selon une légende[7] mesuré les angles d’un triangle formé par trois villes de la région de Hanovre afin de vérifier si la somme de leurs angles constituait effectivement un angle plat.
Démonstrations
Plusieurs centaines de démonstrations différentes[8] ont été répertoriées pour le théorème de Pythagore. La plupart sont construites sur des égalités d’aire obtenues par découpage et recollement, voire en utilisant des rapports d’aire de triangles semblables. La définition du produit scalaire en géométrie repérée fournit aussi une démonstration purement algébrique.
Selon Euclide
La démonstration présentée par Euclide dans les Éléments s’appuie d’une part sur le cas d’égalité[note 2] de deux triangles ayant un angle de même mesure entre deux côtés de mêmes longueurs, d’autre part sur la proposition XLI du livre Ier :
« Si un parallélogramme et un triangle ont une même base, et sont entre mêmes parallèles ; le parallélogramme sera [d’aire] double du triangle. »
Articles détaillés : Triangles isométriques et Aire d'un triangle.DémonstrationSur les côtés d’un triangle ABC rectangle en A, sont construits extérieurement des carrés BCED, ABFG et ACIH. La hauteur de ABC issue de A coupe le côté opposé [BC] en J et le segment [DE] en K.
Il s’agit de démontrer que l’aire du carré BCED est égale la somme des aires des carrés ABFG et ACIH.
Les triangles BCF et ABD ont même angle en B (c’est-à-dire l’angle du triangle ABC augmenté d’un angle droit) et par construction, BF = AB et BC = BD. Donc les triangles BCF et ABD ont même aire. Or d’après la proposition XLI, l’aire du triangle BCF vaut la moitié de celle du carré ABFG et l’aire du triangle ABD vaut la moitié de celle du rectangle BDKJ. Donc le carré ABFG et le rectangle BDKJ ont même aire.
De même, les triangles BCI et ACE ont même angle en C avec les égalités AC = CI et BC = CE donc ils ont même aire, donc d’après la proposition XLI, le carré ACIH a même aire que le rectangle CEKJ.
Finalement, le carré BCED se décompose en deux rectangles BDKJ et CEKJ, dont les aires sont celles de ABFG et ACIH respectivement.Présentation animée de la démonstration d’Euclide
La méthode utilisée permet de démontrer de façon analogue le théorème de Clairaut pour un triangle quelconque sur les côtés duquel sont construits des parallélogrammes.
Par le puzzle de Gougu
Animation du puzzle de Gougu
Le théorème de Gougu[9],[10] de gou (base) et gu (hauteur)(Chemla Shuchun, chap. 9) est reconstitué d’après les commentaires du mathématicien chinois Liu Hui (IIIe siècle apr. J.-C.) sur le JiuZhang SuanShu 九章算術 « neuf chapitres d’Arithmétique » (206 av.–220 apr. J.-C.), et le Zhoubi Suanjian 周髀算經, « l’ombre des cycles, livre de calculs » (un livre d’astronomie). Le neuvième chapitre du livre Les neuf chapitres, classique mathématique de la chine ancienne, s’ouvre sur un énoncé du théorème de Pythagore avec le commentaire laconique : « la base multipliée par elle-même fait un carré vermillon, la hauteur multipliée par elle même un carré bleu-vert et l’on fait en sorte que ce qui entre et ce qui sort se compense l’un l’autre (...) alors (...) on engendre par réunion l’aire du carré de l’hypoténuse ». Cette preuve utilise le principe du puzzle : deux surfaces égales après découpage fini et recomposition ont même aire. Euclide, dans sa propriété de cisaillement, utilise le même principe.
L’absence d’illustration associée à ce commentaire réduisent les historiens à émettre des conjectures pour sa reconstitution. Le dessin ci-contre est proposé par Jean-Claude Martzloff[11] d’après une édition de 1892 des Neuf chapitres. Le triangle rectangle y est tracé en gras, le carré de la hauteur a été tracé à l’extérieur du triangle, le carré de la base et celui de l’hypoténuse sont tournés vers le triangle. Les parties des carrés des côtés de l’angle droit qui dépassent du carré de l’hypoténuse ont été découpées et replacées à l’intérieur de ce carré. Le triangle rouge est égal au triangle de départ. Le triangle jaune a pour grand côté de l’angle droit le petit côté du triangle de départ et a mêmes angles que le triangle initial. Le triangle bleu a pour grand côté de l’angle droit, la différence des côtés du triangle initial et a mêmes angles que le triangle initial.
Karine Chemla(Chemla Shuchun, p. 680) appuie plutôt son raisonnement sur une figure fondamentale associée au texte du Zhoubi suanjing et formée d’un triangle 3 - 4 - 5 dans laquelle on peut lire de nombreuses relations liant les trois côtés du triangle rectangle. Elle interprète le commentaire de Liu Hui comme une nouvelle lecture de la figure fondamentale avec déplacement des 3 pièces 1 - 2 - 3 de l’extérieur du carré dans le carré de l’hypoténuse.
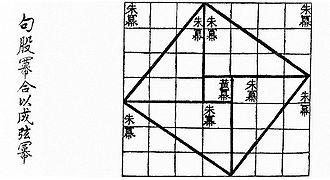 Figure de l’hypoténuse dans laquelle il est aisé de lire[note 3]
Figure de l’hypoténuse dans laquelle il est aisé de lire[note 3]
c² = 4 (ab)/2 +(b - a)²
ou bien aussi
(a + b)² - 4(ab)/2 = c²Quant à Li Jimin[12], il attribue au Zhoubi Suanjian la paternité de la première démonstration, il s’appuie lui aussi sur la figure fondamentale et fait pivoter les triangles (1-2) et 3 sur leur pointe pour les installer dans le carré de l’hypoténuse.
Par soustraction d'aire

Pour un triangle rectangle donné, il est possible de l’inscrire en quatre exemplaires dans les coins d’un carré dont le côté a pour longueur la somme des longueurs des cathètes. Les quatre hypoténuses forment alors un carré, par égalité de longueur et sachant que chacun de ses angles est supplémentaire des deux angles aigus du triangle.
Avec les notations usuelles, l’aire totale du grand carré vaut donc (a + b)2 et l’aire du carré intérieur vaut c2. La différence est constituée par quatre triangle d’aire (ab / 2) chacun.
La relation algébrique s’écrit alors (a + b)2 = 4(ab / 2) + c2, c’est-à-dire a2 + 2ab + b2 = 2ab + c2, ce qui revient à a2 + b2 = c2.
Avec une deuxième figure inscrite dans le même grand carré, les deux carrés formés sur les côtés du triangle rectangle s’obtiennent eux aussi par soustraction de quatre copies du triangle initial.
Par des triangles semblables
Il n’y a pas trace de la démonstration qu’aurait conçue Pythagore et les historiens envisagent deux types de démonstrations : ou bien une démonstration fondée sur un découpage comme celui de Gougu ou une démonstration utilisant les proportionnalités des triangles découpés par la hauteur issue de l’angle droit[13].
Si H est le pied de la hauteur issue de C, les triangles CAB, HAC et HCB sont semblables (par égalités des angles). Le rapport de similitude entre les triangles HAC et CAB est le rapport des hypoténuses AC/AB, de même le rapport de la similitude entre les triangles HCB et CAB est CB/AB. Le rapport des aires est alors égal au carré du rapport de la similitude, soit :
 et
et  .
.Comme d’autre part la somme des aires des triangles HAC et HCB donne l’aire du triangle CAB, on peut écrire :
 . Soit encore : AC2 + BC2 = AB2.CQFD
. Soit encore : AC2 + BC2 = AB2.CQFDOn peut également proposer une variante plus élémentaire de cette démonstration afin de s’affranchir de la notion d’aire : Le rapport de similitude entre les triangles HAC et CAB implique
 soit
soit  . De même, le rapport de similitude entre les triangles HCB et CAB implique
. De même, le rapport de similitude entre les triangles HCB et CAB implique  soit
soit  en additionnant, il vient
en additionnant, il vient  . CQFD
. CQFDCette démonstration est à rapprocher de celle du théorème de Ptolémée en prenant un rectangle comme quadrilatère.
Par le produit scalaire
Dans le plan muni d’un repère orthonormé, les vecteurs portés par les côtés d’un triangle ABC vérifient la relation de Chasles :
donc par bilinéarité du produit scalaire, il vient :
donc la relation du théorème est équivalente à l’annulation du dernier produit scalaire, ce qui correspond précisément au cas où les vecteurs sont orthogonaux, autrement dit lorsque les côtés [AC] et [BC] forment un angle droit.
Généralisations
Pour un triangle quelconque
Le théorème d'Al-Kashi donne une formule faisant intervenir les longueurs des côtés et le cosinus d’un angle. L’angle de mesure γ, le côté opposé de longueur c et les deux autres côtés de longueurs respectives a et b sont reliés par la relation :
 .
.
Si l’angle γ est droit, son cosinus est nul et la formule se réduit à la relation du théorème de Pythagore.
Cette formule est liée à la bilinéarité du produit scalaire. Elle permet de traiter des problèmes de calcul d’angles et de distances avec les autres relations métriques du triangle données par le théorème de la médiane, la formule de l’aire et la loi des sinus.
Avec d'autres figures formées sur les côtés
Euclide mentionne dans les Éléments[4] (proposition 31 du livre VI) :
-
Dans les triangles rectangles, la figure construite sur l’hypoténuse est équivalente à la somme des figures semblables et semblablement construites sur les côtés qui comprennent l’angle droit.
 Propriété des lunules
Propriété des lunules
En appliquant cette généralisation à des demi-disques formés sur chaque côté d’un triangle rectangle, il en découle le théorème des deux lunules, selon lequel l’aire du triangle rectangle est égale à la somme des aires des lunules dessinées sur chaque côté de l’angle droit.
Le théorème de Clairaut est une autre généralisation, valable sur un triangle quelconque, sur les côtés desquels sont construits des parallélogrammes.
En plus grande dimension
L’hypoténuse d’un triangle rectangle pouvant se concevoir comme la diagonale d’un rectangle, une généralisation du théorème en dimension supérieure peut s’énoncer comme suit :
- Dans un pavé droit, le carré de la grande diagonale est égal à la somme des carrés des dimensions du pavé.
Ce résultat est équivalent au calcul de la longueur d’un segment à partir des coordonnées cartésiennes de ses extrémités dans un repère orthonormé :
ou, en dimension supérieure, si A est de coordonnées (xi) et B de coordonnées (x'i) :
 .
.
Cette dernière formule est encore valable dans un espace de Hilbert de dimension infinie et aboutit notamment à la formule de Parseval.
Le théorème de Gua donne une autre généralisation du théorème de Pythagore dans un espace euclidien : si un tétraèdre a toutes ses arêtes orthogonales en un sommet alors le carré de l’aire de la face opposée au coin est la somme des carrés des aires des trois autres faces.
En géométrie non euclidienne
Le théorème de Pythagore est équivalent à l'axiome des parallèles, qui peut être rédigé ainsi :
Axiome des parallèles — Par un point, il passe une et une seule droite parallèle à une droite donnée.
Cela signifie que, dans les axiomes de la géométrie euclidienne, on peut remplacer l'« axiome » des parallèles par le « théorème » de Pythagore sans que les autres résultats de la géométrie soient modifiés. Les statuts d'axiome et de théorème de ces deux résultats sont alors inversés : le « théorème » de Pythagore devient un axiome (une vérité de base, indémontrable, sur laquelle s'appuie la théorie) et l'« axiome » des parallèles devient un théorème, qui peut être démontré à l'aide de Pythagore.
Dans d'autres géométries, l'axiome des parallèles est remplacé par un autre, et le théorème de Pythagore n'est donc plus vrai.
En géométrie sphérique, si un triangle est formé par trois arcs de grands cercles à la surface d’une sphère de rayon R et si deux de ces arcs se croisent à angle droit, la relation du théorème de Pythagore n’est plus valable, comme dans le cas du triangle équilatéral trirectangle. Elle doit être remplacée par la formule :
où c est la longueur de l’arc opposé à l’angle droit.
Une relation similaire existe en géométrie hyperbolique pour une courbure constante égale à −1 :
où ch désigne la fonction cosinus hyperbolique.
Dans les deux cas, un développement limité à l’ordre 2 redonne, pour des triangles de faible dimension, la relation du théorème de Pythagore en géométrie plane.
Plus généralement, la propriété résiste mal au transfert dans d’autres géométries à cause de leur courbure :
- si la courbure est positive : c2 < a2 + b2 ;
- si la courbure est négative : c2 > a2 + b2 ;
- si la courbure est nulle : c2 = a2 + b2.
Dans le cadre de la relativité générale, l’espace euclidien est remplacé par un espace courbe où les segments sont remplacés par des géodésiques. La théorie de la relativité générale soutient que la matière et l’énergie conduisent l’espace à être non-euclidien et le théorème ne s’applique donc pas strictement en présence d’énergie. Cependant, la déviation par rapport à l’espace euclidien est faible sauf auprès d’imposantes sources gravitationnelles comme les trous noirs. Déterminer si le théorème est enfreint sur d’importantes échelles cosmologiques, c’est-à-dire mesurer la courbure de l’Univers, est un problème ouvert pour la cosmologie.
Culture
Le théorème de Pythagore est mentionné dans La Planète des singes, de Pierre Boulle. Le narrateur, considéré comme un animal dépourvu d’intelligence, détrompe en effet son interlocuteur en traçant une figure géométrique qui illustre le théorème.
Le chansonnier Franc-Nohain a composé un quatrain qui cite le théorème[14] :
Le carré de l’hypoténuse
Est égal, si je ne m’abuse
À la somme des carrés
Construits sur les autres côtés.Notes et références
Notes
- L’incommensurabilité du côté et de la diagonale du carré peut cependant se démontrer sans recourir au théorème de Pythagore.
- L’expression est utilisée pour désigner des triangles isométriques.
- Le commentaire du Zhoubi suanjing consiste à remarquer que le carré de l’hypoténuse est formé de 4 triangles vermillon d’aire ab/2 et d’un carré jaune central d’aire (b-a)²
Références
- Le mathématicien Van der Waerden Le problème des objets dans la ... - Google Livres et l’ingénieur Alexander Thom Les mégalithes, ésotérisme et réalité - Google Livres auraient découvert des triplets pythagoriciens sur des sites mégalithiques en Grande-Bretagne et à Carnac, mais leurs analyses sont contestées par Kaveing et Keller [1].
- Voir le texte de Plutarque et les travaux de Jean Philippe Lauer relatés dans La géométrie égyptienne de Théophile Obenga.
- André Demailly attribue déjà cette compétence aux arpenteurs égyptiens dans Herbert Simon et les sciences de conception. C’est même ainsi que Thomas Henri Martin imagine la diffusion de ce savoir aux Grecs et aux Chinois dans Les signes numéraux chez les peuples de l’Antiquité et du Moyen Âge.
- Éléments d’Euclide
- Référence
- document en ligne sur le site de la BNF (Ressources Gallica) Livre I : cisaillement proposition XXXV p. 62 ; parallélogramme et triangle de même base : proposition XLI p. 69 ; figure dite du moulin à vent : proposition XLVII p. 76 ; réciproque : proposition XLVIII p. 78 ; Livre VI : couper une ligne selon moyenne et extrême raison proposition XXXI p. 241
- Entrée « Irrationnel » § III b dans (Baruk 1992).
- (en) Scott E. Brodie, « The Pythagorean Theorem is Equivalent to the Parallel Postulate », cut-the-knot
- Voir Renaissance de la géométrie non euclidienne entre 1860 et 1900, par Jean-Daniel Voelke, page 40 et suivantes ; Gauss a explicitement déclaré que seules des mesures sur des distances « immensément supérieures au rayon de la Terre » permettraient une telle vérification.
- Le site (en) Alexander Bogomolny, « Pythagorean theorem », cut-the-knot, propose 92 démonstrations différentes du théorème mais cite The Pythagorean Proposition (par Elisha Scott Loomis, au début du XXe siècle) qui en rassemble 367.
- (en) Proof of Guogu or Pythagoras' Theorem sur chinapage.com
- Quelques exemples de démonstration en mathématiques chinoises, Jean-Claude Martzloff, in La démonstration mathématique dans l’histoire, Irem de Lyon
- Jean-Claude Martzloff, Une histoire des mathématiques chinoises, A history of chinese mathematics - Google Livres
- Karine Chemla dans (Chemla Shuchun) fait référence à l’interprétation (1993) de cet historien p. 682.
- Eliane Cousquer, Le Théorème de Pythagore[PDF] sur le site mediamaths
- Entrée « Pythagore (théorème de) » dans (Baruk 1992)
Sources
- Karine Chemla et Guo Shuchun, Neuf Chapitres. Le Classique de la Chine ancienne et ses commentaires. Édition critique. [détail des éditions],
- Stella Baruk, Dictionnaire de mathématiques élémentaires, 1992 [détail de l’édition]
Annexes
Articles connexes
- Contexte
- Problèmes reliés
- Généralisations
- Théorème de Clairaut (géométrie), un cas plus général, avec des parallélogrammes autour d’un triangle quelconque
- Théorème d'Al-Kashi (Le théorème de Pythagore généralisé) avec un peu de trigonométrie
- Ouverture
Catégories :- Théorème de géométrie
- Géométrie du triangle
- Histoire des mathématiques
- Mathématiques élémentaires
Wikimedia Foundation. 2010.









![Figure dite du moulin à vent, avec un triangle ABC sur les côtés duquel sont formés trois carrés BCED, ABFG et ACIH. La hauteur de ABC issue de A coupe [BC] en J et [DE] en K.](/pictures/frwiki/50/260px-PythagoreEuclide0.svg.png)