Entier quadratique

Pour les articles homonymes, voir Entier (homonymie).

En mathématiques, un entier quadratique est un nombre réel ou complexe, racine d'un polynôme du second degré à coefficients dans les nombres entiers et dont le coefficient du terme du plus haut degré est égal à 1. Un irrationnel quadratique est une notion un peu équivalente. Elle correspond encore à un nombre réel (non rationnel) ou complexe, racine d'un polynôme du second degré à coefficients rationnels, cette fois quelconque.

Ces nombres particuliers disposent de propriétés algébriques. Si α est un entier quadratique, l'ensemble des nombres de la forme a + b.α, où a et b désignent deux nombres entiers, est stable pour l'addition, la soustraction et la multiplication. Un tel ensemble est qualifié d'anneau. Si β est un irrationnel quadratique, l'ensemble des nombres de la forme a + b.β, où a et b désignent deux nombres rationnels, est stable pour les quatre opérations, on parle cette fois de corps.

Un nombre quadratique, entier ou irrationnel, est ainsi avant tout un élément d'un ensemble, structuré par deux opérations. Cette approche est au cœur de la théorie algébrique des nombres. Au lieu d'étudier un nombre particulier, comme le nombre d'or, l'analyse de la structure d'anneau associé, ici celui des entiers du corps Q( $\sqrt 5$ ) est plus fructueuse. Cette démarche est ancienne, dès le VI^e siècle les mathématiciens indiens avaient déjà découvert une multiplication sur un ensemble de cette nature, qui permet de résoudre certains cas particuliers de l'équation de Pell-Fermat. Gauss, un mathématicien du XIX^e siècle, préfigure la démarche moderne et fixe le vocabulaire avec l'étude des entiers portant maintenant son nom. Il découvre que cet anneau est euclidien, permettant de développer une arithmétique analogue à celle des entiers relatifs, avec sa version du théorème fondamental de l'arithmétique et ses nombres premiers.

Ces structures sont parfois sujettes à une difficulté, qualifiée d'obstruction. Elle concerne les éléments inversibles pour la multiplication, ils sont parfois en nombre infini. Une deuxième obstruction existe si l'anneau n'est pas euclidien. L'unicité de la décomposition en facteurs premiers ne s'applique plus et les techniques usuelles de l'arithmétique s'avèrent inopérantes. Une analyse plus profonde de la structure de l'anneau permet d'y remédier à l'aide du concept d'idéal.

Les anneaux d'entiers quadratiques forment en général la première classe d'exemples dans laquelle on tente de faire fonctionner des théories inaccessibles dans le cas général (voir par exemple le théorème de Kronecker-Weber en théorie des corps de classes). L'étude des entiers quadratiques admet une version plus algébrique : l'étude des formes quadratiques à coefficients entiers (en). Il n'y a pas^{[réf. nécessaire]} d'analogue à cette interprétation dans les corps de nombres en général.

Préambule

Motivation

La première motivation historique est la résolution d'équations diophantiennes du deuxième degré. Ces équations sont à coefficients entiers et les solutions recherchées sont entières. Un exemple célèbre est x² - 61.y² = 1, traité^[1] par Brahmagupta, un mathématicien indien, reprise par Fermat dans un défi présenté à la communauté européenne en 1657^[2].

En vue de résoudre cette équation, il est judicieux d'étudier les nombres de la forme a + b $\sqrt 6$ 1, ici a et b désignent deux entiers relatifs. On remarque que si α et β sont de cette forme, alors leur somme et leur produit l'est aussi. De plus, si α et β correspondent à deux couples d'entiers solutions de l'équation, alors c'est aussi le cas pour α.β. Résoudre l'équation revient en fait à déterminer un sous-ensemble particulier de l'anneau des entiers quadratiques de la forme a + b $\sqrt 6$ 1. Cet ensemble correspond à un sous-groupe du groupe des unités, c'est-à-dire des éléments possédant un inverse dans l'anneau.

Un deuxième exemple est l'étude des propriétés arithmétiques associées au nombre d'or φ. Une fois encore, les nombres de la forme a + b.φ forment une structure stable pour l'addition et la multiplication, appelé anneau. Il est particulier dans le sens où il admet une division euclidienne. Cette division euclidienne offre une structure suffisamment proche de celle des entiers relatifs pour que le terme d' entier soit utilisé pour écrire un élément de l'ensemble. Les techniques de résolution sont absolument analogues à celle de l'arithmétique élémentaire.

Pour Z, il est utile d'enrichir la structure pour obtenir un ensemble munis d'une addition et d'une multiplication tel que tout élément non nul soit inversible. La technique utilisée, appelée corps des fractions permet de construire Q, le corps des nombres rationnels. Elle s'applique aussi aux anneaux d'entiers quadratiques. On obtient une structure dont les éléments sont appelés parfois rationnels quadratiques par analogie avec les nombres rationnels obtenus à partir des entiers relatifs. À travers le concept de tour d'extension quadratique, cette structure est l'un des fondements de la compréhension des figures constructibles à la règle et au compas.

Anneaux euclidiens

Article détaillé : Anneau euclidien.

Les entiers algébriques sur un corps quadratique forment des anneaux aux propriétés variables en fonction d'une valeur d correspondant à un entier sans facteur carré.

Si d est égal à -1, l'anneau est celui des entiers de Gauss. Il est formé des nombres complexes de la forme a + i.b avec a et b deux entiers relatifs et i l'unité imaginaire. Il correspond à une structure simple, il est euclidien et en conséquence principal et factoriel. Le groupe des unités est fini et cyclique. Cette configuration se produit pour quelques valeurs de d comme -2 et -3. Si d est égal à -3, l'anneau est celui des entiers d'Eisenstein. Sur chacun de ces anneaux, les outils de l'arithmétique élémentaire s'appliquent avec succès. Le lemme d'Euclide, l'identité de Bézout ou encore la décomposition en facteurs premiers se traduisent pratiquement sans modification. Ceux plus sophistiqués de l'arithmétique modulaire comme le passage au quotient, le petit théorème de Fermat ou la loi de réciprocité quadratique se généralisent aussi sans difficulté majeure.

Groupe des unités

Article détaillé : Groupe des unités.

Si d est positif, une première difficulté apparait, elle est illustrée par l'anneau des entiers de Dirichlet qui correspond à l'arithmétique du nombre d'or (1 + $\sqrt 5$ )/2. Cette arithmétique est étudiée en profondeur à l'aide des outils élémentaires dans l'article associé. Si l'anneau est parfois euclidien, le groupe des unités devient infini. Pour toutes ces valeurs, aucun des théorèmes ou propriétés cités précédemment n'est utilisable. Pour la résolution d'équations diophantiennes comme celle du grand théorème de Fermat pour n = 5, les contournements deviennent acrobatiques. Comprendre la structure du groupes des unités revient à résoudre l'équation de Pell-Fermat. Dirichlet appelle obstruction cette difficulté. Si d est négatif, cette difficulté n'apparaît jamais, le groupe des unités est fini et cyclique.

Anneaux non factoriels

Article détaillé : Anneau factoriel.

Si la valeur absolue de d augmente, une deuxième obstruction voit le jour. Le cas où d est égal à -5, l'anneau des entiers est Z[i. $\sqrt 5$ ] est le premier exemple. Il correspond au plus petit anneau contenant l'ensemble des entiers relatifs Z et i. $\sqrt 5$ . L'égalité suivante met en évidence cette obstruction :

$2.3=(1+i.\sqrt 5)(1-i.\sqrt 5)\;$

Aucun des quatre entiers de l'égalité précédente ne possède de diviseur autre de 1 et lui-même (au groupe des unités près). Ils correspondraient donc à des nombres premiers. L'égalité montre que 6 possède dans cet anneau deux décompositions en facteurs premiers. L'anneau n'est ni euclidien, ni principal ni factoriel. D'autres outils doivent être mis en jeu pour appréhender cette situation.

Caractérisation

Irrationnel quadratique

L'un des objets de l'article est l'étude des nombres répondant à la définition suivante :

Un irrationnel quadratique est un nombre complexe non rationnel solution d'une équation du second degré à coefficients rationnels.

Il existe une manière simple de caractériser les nombres quadratiques :

Un nombre α est irrationnel quadratique si, et seulement si, il existe deux rationnels a et b, tel que b soit non nul, et un entier sans facteur carré d tel que α est égal à a + b. $\sqrt d$ .

Il existe une convention prise ici, que les analystes ne font pas. Il n'est dit nulle part que d est un entier positif, ce qui sous-entend que l'expression $\sqrt d$ peut décrire la racine carrée d'un nombre négatif. En analyse, cette situation est dangereuse, on ne sait pas si cette racine désigne i. $\sqrt - d$ ou -i. $\sqrt - d$ et il n'est pas possible d'adopter une convention qui rende la fonction racine continue sur l'ensemble des nombres complexes. Le paragraphe suivant montre que cette difficulté n'existe pas dans le contexte de cet article. Pour une raison de commodité, l'usage du radical racine pour des entiers négatifs est fréquent en théorie algébrique des nombres^[3], cette convention est utilisée ici.

Si α est solution d'une équation du second degré à coefficients rationnels alors la technique de résolution de cette équation à l'aide d'un discriminant montre qu'il existe trois rationnels a, c et e tel que α = a + c. $\sqrt e$ . Si e est une fraction dont un représentant est f / g, quitte à multiplier en haut et en bas de la fraction par les facteurs non carrés du dénominateur, il est possible d'écrire e sous la forme d'un entier divisé par un carré parfait. Il est alors possible de sortir le dénominateur du radical. On peut donc choisir e entier. Si e contient des facteurs carrés, il est encore possible de les sortir du radical, on obtient alors une expression de la forme a + b. $\sqrt d$ , où a et b sont des nombres rationnels et d un entier sans carré parfait. Comme le nombre α n'est pas choisi rationnel, le coefficient b n'est pas nul.

Réciproquement si α est égal à a + b. $\sqrt d$ , il est solution de l'équation suivante :

$X^2 - 2a X + (a^2 - db^2) = 0 \;$

Corps quadratique

Article détaillé : Extension quadratique.

Le nombre d désigne dans le reste de l'article un entier sans facteur carré, la lettre Z désigne l'anneau des nombres entiers, Q le corps des rationnels, R celui des réels et C celui des complexes.

L'intérêt de la notion de nombre quadratique provient de structures algébriques sous-jacentes à ce nombre. On étudie plus les propriétés des structures associées que le nombre lui-même. Une des structures essentiels correspond au plus petit ensemble contenant l'irrationnel quadratique, contenant 1 et stable par addition, soustraction, multiplication et division. Évidemment, cette stabilité ne concerne pas la division par 0.

L'ensemble des nombres de la forme x + y. $\sqrt d$ est généralement noté Q[ $\sqrt d$ ], les résultats précédents s'expriment, en terme mathématiques, par le fait que Q[ $\sqrt d$ ] dispose d'une structure de corps commutatif.

Un corps quadratique K est un sous-corps du corps des complexes tel qu'il existe un entier sans facteur carré d et K est égal à Q[ $\sqrt d$ ]. Un élément de ce corps est appelé nombre quadratique.

Ainsi les définitions de nombre quadratique et irrationnel quadratique sont très similaires. Tout irrationnel quadratique est un nombre quadratique, réciproquement, un nombre quadratique non rationnel est un irrationnel quadratique. On peut imaginer définir un corps quadratique différemment, comme un corps ne contenant que des nombres quadratiques. La proposition suivante montre qu'une telle démarche est licite.

Soit un corps commutatif K contenant Q mais non restreint à Q et qui ne contienne que des nombres quadratiques. Il existe un entier d, sans facteur carré, tel que K soit isomorphe à Q[ $\sqrt$ d].

Les algébristes construisent souvent le corps K d'une autre manière. Ils considèrent tout d'abord l'anneau des polynômes à coefficients dans les rationnels. Comme l'ensemble Q des rationnels est un corps, cet anneau est euclidien. Le polynôme X² - d est irréductible si d est un entier sans facteur carré. Irréductible signifie qu'il ne peut pas s'exprimer comme un produit de deux polynômes de degré 1. L'Idéal engendré par X² - d est un idéal maximal car l'anneau des polynômes est euclidien, donc principal, et le quotient de l'anneau des polynômes par cet idéal maximal est un corps. Tout élément de ce corps s'écrit x + y. $\sqrt d$ si $\sqrt d$ désigne la classe du polynôme X. Le signe de d ne modifie en rien la validité de la construction. Comme X² - d est dans l'ideal quotient, la classe de X possède un carré égal à d, qu'il soit positif ou négatif, ce qui justifie la notation. Elle est d'autant plus cohérente que ce corps est une copie, le terme exact est isomorphe, du plus petit sous-corps de C contenant $\sqrt d$ ou i. $\sqrt - d$ si d est négatif.

Démonstration

Le plus petit sous-corps contenant le nombre quadratique a + b. $\sqrt d$ est K[d] :

Comme cet ensemble est stable par addition et soustraction et contient 1, il contient tous les entiers. Comme il est stable par division, il contient tous les rationnels. Par hypothèse il contient le nombre quadratique a + b. $\sqrt d$ , en additionnant -a, on remarque qu'il contient b. $\sqrt d$ et en divisant par b, il contient aussi $\sqrt d$ . Il contient donc 1 et $\sqrt d$ , et nécessairement tous les nombres de la forme x + y. $\sqrt d$ , où x et y décrivent l'ensemble des rationnels.

Réciproquement, l'ensemble des nombres de la forme x + y. $\sqrt d$ contient 1 et a + b. $\sqrt d$ . Il est stable pour les quatre opérations. La stabilité de l'addition et de la soustraction est évidente, celle de la multiplication provient de la propriété suivante :

$\forall x_1,y_1,x_2,y_2 \in\Q\quad (x_1 + y_1\sqrt d)(x_2 + y_2\sqrt d)= x_1x_2 + dy_1y_2 + (x_1y_2 + x_2y_1)\sqrt d$

Il faut encore vérifier que tout élément non nul admet bien un inverse dans cet ensemble. On remarque tout d'abord que x² - d.y² ne peut être nul. S'il l'était alors d serait un quotient de carrés parfaits or d est un entier sans facteur carré. Il suffit alors de remarquer que si x et y est un couple de rationnels non tous les deux nuls :

$(x + y\sqrt d)\left(\frac x{x^2 - dy^2} - \frac y{x^2 - dy^2}\sqrt d \right)= 1$

Soit un corps commutatif K contenant Q mais non restreint à Q qui ne contiennent que des nombres quadratiques. Il existe un entier d, sans facteur carré, tel que K soit isomorphe à Q[ $\sqrt d$ ] :

La théorie de Galois permet de résoudre cette question très simplement en faisant appel au théorème de l'élément primitif. Il suffit de considérer n'importe qu'elle extension finie de Q dans K, elle admet un élément primitif, elle est donc de degré 2. Le corps K n'admet que des sous-corps de degré 2 sur Q, il est donc de degré 2.

Il est néanmoins possible de démontrer sans outil puissant ce petit résultat. Nous savons a priori quatre choses sur le corps K : qu'il est commutatif, de caractéristique nulle et que tout élément est racine d'un polynôme de degré inférieur ou égal à 2 à coefficients dans son corps caractéristique et qu'il contient un élément qui n'est pas dans le corps caractéristique.

La caractéristique d'un corps est égal au plus petit entier n, tel que 1, additionné n fois à lui-même soit égal à 0. Si un tel n n'existe pas, le corps est qualifié de caractéristique nulle. Le corps caractéristique est le plus petit sous-corps de K. Il contient nécessairement 1 et donc le sous corps engendré par 1. Si le corps est de caractéristique nulle, il contient une copie de Z et nécessairement une copie de Q. On identifie en général cette copie avec Q ce que nous faisons ici.

Dans le cas présent, il existe un élément α qui n'est pas dans Q, cet élément est racine d'un polynôme de degré 2, à coefficients dans Q et irréductible. Il est donc de la forme a + $\sqrt d$ .b où a et b sont des rationnels et $\sqrt d$ un nombre tel que son carré est égal à d, un élément de Q. La même approche que celle utilisée précédemment montre que d peut être choisi entier sans facteur carré. Soit α₁ un élément quelconque de K, l'objectif est de montrer qu'il existe deux rationnels a₁ et b₁ tel que α₁ = a₁ + b₁. $\sqrt d$ .

Si α₁ est rationnel l'objectif est immédiatement atteint. Supposons qu'il ne le soit pas. Le même raisonnement que précédemment montre que α₁ = a₁ + b₁. $\sqrt f$ où f est encore un entier sans facteur carré. Il suffit donc de montrer que f est égal à d. Pour cela remarquons que $\sqrt d$ et $\sqrt f$ sont deux éléments de K leur somme est encore élément de K, donc solution d'une équation du second degré à coefficients dans Q.

Soit P(X) = X² + hX + k un polynôme à coefficients dans Q et ayant $\sqrt d$ + $\sqrt f$ comme racine. On dispose de l'égalité suivante :

$d + f + 2\sqrt {df} + h(\sqrt d + \sqrt f) + k = 0 \quad\text{et}\quad d + f + k + h\sqrt d = \sqrt f(h + 2\sqrt d)$

On remarque que h + 2 $\sqrt d$ ne peut être nul car $\sqrt d$ n'est pas rationnel alors que h l'est. On en déduit que $\sqrt f$ est le quotient de deux éléments de Q[ $\sqrt d$ ], ce qui montre qu'il est élément de Q[ $\sqrt d$ ] et :

$\exists h_1, k_1 \in\Q \quad \sqrt f = h_1 + k_1\sqrt d \quad\text{et}\quad f = h_1^2 + dk_1^2 + 2h_1k_1\sqrt d$

Ceci montre qu'un rationnel multiplié par $\sqrt d$ est un rationnel. Le seul rationnel ayant cette propriété est 0, et soit h₁ soit k₁ est nul. Si k₁ est nul, $\sqrt f$ est rationnel, ce qui est contraire aux hypothèses, donc h₁ est nul et $\sqrt f$ = k₁ $\sqrt d$ , et f est égal à k₁².d. Or f est un entier sans facteur carré, donc k₁ est égal à 1 et f à d.

Il est temps de conclure. K contient Q[ $\sqrt d$ ] car c'est un corps contenant $\sqrt d$ . Réciproquement tout élément de K est contenu dans Q[ $\sqrt d$ ] d'après l'analyse précédente. Les deux structures sont bien égales.

Entier quadratique

Un des charmes d'un corps quadratique, général à tout corps algébrique, est qu'il présente une structure un peu analogue à celle des nombres rationnels. Tout comme les nombres rationnels disposent d'entiers, un corps quadratique dispose aussi d'entiers, la définition peut néanmoins paraître un peu étrange en premier abord, la suite montre qu'elle est parfaitement justifiée :

Un entier quadratique est un élément d'un corps quadratique dont le polynôme minimal est à coefficients dans Z.

Le polynôme minimal d'un nombre α est le polynôme à coefficients rationnels de plus petit degré, de monôme dominant ayant un coefficient égal à 1 et ayant α pour racine. L'article sur ce concept montre qu'il est unique et tout polynôme à coefficients rationnels ayant α pour racine est un multiple du polynôme minimal. Un irrationnel quadratique possède un polynôme minimal nécessairement de degré 2, un entier algébrique peut aussi être rationnel et posséder un polynôme minimal de degré 1, cette différence subtile, permet de considérer un élément de Z comme un entier quadratique. Il serait étrange de considérer 1 comme non entier et 1/2 comme un irrationnel quadratique, d'où la différence dans la définition.

L'article entier algébrique correspondant à la généralisation du concept pour un corps algébrique quelconque montre que les seuls entiers algébriques de Q sont les éléments de Z. L'analogie va plus loin :

La somme, la différence et le produit de deux entiers algébriques est un entier algébrique.

Cette situation est encore comparable à celle de Z. On peut encore dire que l'ensemble des entiers algébriques d'un corps quadratique forme un anneau. Cette situation est la même pour tous les corps algébriques, d'où une définition générale :

L' anneau des entiers d'un corps algébrique K est appelé fermeture intégrale de Z dans K et est souvent noté O_K^[4].

Il est intéressant de caractériser l'ensemble des entiers algébriques d'un corps quadratique :

Si d est congru à 1 modulo 4, alors l'anneau des entiers algébrique de Q[ $\sqrt d$ ] est égal à Z[(1 + $\sqrt d$ ) / 2], sinon l'anneau est égal à Z[ $\sqrt d$ ].

L'expression, Z[ $ω$ ] désigne l'ensemble des nombres de la forme a₀ + a₁.ω + a₂.ω² + ... + a_n.ωⁿ, où a₀, a₁, ..., a_n sont des éléments de Z. Ici, ω² s'écrit toujours comme une combinaison linéaire à coefficients dans Z de 1 et de ω, elle est donnée par le polynôme minimal, si ω désigne une des valeurs de l'énoncé de la proposition, à savoir (1 + $\sqrt d$ ) / 2 ou bien $\sqrt d$ . Dans toute la suite de l'article ω désigne cette valeur. Un élément de l'anneau Z[ω] est donc de la forme a + ω.b, où a et b sont des éléments de Z.

Démonstrations

Supposons que d ne soit pas congru à 1 modulo 4 :

Soit a et b deux entiers relatifs et v = a + b. $\sqrt d$ , alors v est racine du polynôme P(X) suivant et est donc algébrique :

$P(X)= X^2 - 2a.X + a^2 - d.b^2\;$

Réciproquement, supposons w algébrique, il existe deux rationnels α et β tel que w = α + β. $\sqrt d$ et si le polynôme minimal de w est noté Q(X) alors :

$Q(X)= X^2 - 2\alpha.X + \alpha^2 - d.\beta^2\quad \text{et}\quad 2\alpha\in\Z\; ,\quad \alpha^2 - d.\beta^2\in\Z$

les nombres 2.α et 4(α² - d.β²) sont des entiers relatifs et 4.d.β² l'est aussi. Comme d ne contient aucun facteur carré, 2.β est un entier relatif.

Si d est congru à 2 modulo 4, alors 2.d.β² est élément de Z et 2.α² aussi, comme 2.α est un entier relatif, α l'est aussi. On en déduit que d.β² est un entier relatif, comme d n'est pas un multiple de 4, et que 2.β est un entier relatif, β l'est aussi.

Si d est congru à 3 modulo 4, (2.α)² - d.(2.β)²) est un multiple de 4, si (2.β) est impair, alors (2.β)² est congru à 1 modulo 4, d.(2.β)² est congru à 3 modulo 4 et (2.α)² - d.(2.β)²) est congru à 2 modulo 4, ce qui est impossible, c'est un multiple de quatre. On en déduit que 2.β est pair et β est entier. Ceci montre que d.(2.β)² est un multiple de 4, et donc (2.α)² aussi, on en déduit que α est entier.

Supposons que d soit congru à 1 modulo 4 :

Soit a et b deux entiers relatifs et v = a + b(1 + $\sqrt d$ )/2, alors v est racine du polynôme P(X) suivant et est donc entier algébrique car d - 1 est un multiple de quatre :

$P(X)=X^2 - (2a+b).X + a^2 + a.b - b^2\frac{d-1}4$ .

Réciproquement, supposons w algébrique, il existe deux rationnels α et β tel que w = α + β.(1 + $\sqrt d$ )/2 et si le polynôme minimal de w est noté Q[X] alors :

$Q[X] = X^2 - (2\alpha + \beta).X + \alpha^2 + \alpha.\beta - \beta^2\frac{d-1}4\quad \text{et}\quad 2\alpha + \beta\in\Z\; ,\quad (\alpha + \frac\beta 2)^2 - \beta^2\frac d4\in\Z$ .

On en déduit que (2α + β)² - d.β² est un multiple de 4, comme 2α + β est un entier relatif, d.β² l'est aussi. Comme d ne contient aucun facteur carré, β est un entier relatif. Comme (2α + β)² - d.β² est un multiple de quatre et que β est un entier relatif, 4(α² + α.β) est un multiple de 4 (car d - 1 est un multiple de quatre) et (2α)² + 2.(2.α).β est un multiple de 4. Comme 2α + β et β sont des entiers relatifs, 2α l'est aussi. Si 2α est impair, alors (2α)² + 2.(2.α).β est impair, or cette valeur est un multiple de 4, donc α est un entier relatif, ce qui termine la démonstration.

La fermeture intégrale de Z dans un corps quadratique est un anneau :

L'ensemble considéré est manifestement un groupe abélien, il suffit donc de montrer la stabilité pour la multiplication, les autres propriétés se déduisent du fait que la fermeture intégrale est une partie d'un corps. Soit d un entier relatif sans facteur carré, les deux égalités suivantes montrent que dans tous les cas, la fermeture est stable par multiplication :

$\forall a,b,a',b'\in\Z\quad (a + b.\sqrt d)(a' + b'.\sqrt d)= aa' + d.bb' +(ab'+ba')\sqrt d \;$ $\forall a,b,a',b'\in\Z\quad (a + b\frac{1+\sqrt d}2)(a' + b'\frac{1+\sqrt d}2)= aa' + \frac {d -1}4.bb' +(ab'+ba')\frac{1+\sqrt d}2\;$

Fermeture intégrale et clôture intégrale

La configuration est celle du corps, ici un corps quadratique, contenant un anneau, celui des entiers quadratiques. Elle ressemble un peu à celle de Q et Z à cet égard. La relation entre Z et Q est aussi caractérisée par le fait que Q est le corps des fractions de Z, c'est-à-dire le plus petit corps contenant Z. En fait, Q est construit comme l'ensemble des couples (a, b); où a est un entier et b un entier non nul, quotienté par une relation d'équivalence. On peut appliquer la même méthode à l'anneau des entiers d'un corps quadratique pour rechercher le plus petit corps contenant cet anneau.

Le corps des fractions de l'anneau des entiers d'un corps quadratique Q[ $\sqrt d$ ] est isomorphe à Q[ $\sqrt d$ ].

Pour cette raison le terme de rationnel quadratique désigne un élément de ce corps. Un rationnel quadratique est un nombre quadratique, il correspond soit à un irrationnel quadratique, soit à un élément de Q. Comme précédemment, on peut se poser la question de la forme d'un anneau unitaire (c'est-à-dire qui contient l'élément 1) composé uniquement d'entiers quadratiques. La situation est un peu différente que celle de Q et Z, ici il existe d'autres anneaux, toujours inclus dans une fermeture intégrale :

Soit A un anneau unitaire contenant strictement Z et formé uniquement d'entiers quadratiques. Il existe un entier d, non carré parfait, tel que A est égal à Z[ω] ou ω est égal soit à $\sqrt d$ soit, si d est congru à 1 modulo 4, à (1 + $\sqrt d$ ) / 2.

La nuance provient de la nature de d. Dans une fermeture intégrale d est un entier sans facteur carré, comme 2 ou -6. Dans la proposition précédente d est un entier non carré parfait comme 18 ou -12. Or 18 et -12 ne sont pas des entiers sans facteur carré. Ainsi le corps Q[ $\sqrt 3$ ] contient l'anneau Z[ $\sqrt 3$ ] mais aussi Z[ $\sqrt 12$ ]. Cette différence donne lieu à la définition suivante :

Un anneau d'entiers quadratiques est dit intégralement clos si et seulement s'il est égal à sa clôture intégrale.

Le corps des fractions de Z[ $\sqrt 12$ ] contient $\sqrt 3$ et est en fait égal à Q[ $\sqrt 3$ ]. L'anneau des entiers de Q[ $\sqrt 3$ ] est égal à Z[ $\sqrt 3$ ] qui contient strictement Z[ $\sqrt 12$ ], qui n'est ainsi pas intégralement clos. Les anneaux intégralement clos sont les plus riches en propriétés. Par contre, Z[ $\sqrt -3$ ] n'est pas un anneau euclidien, ni même factoriel. Pour s'en rendre compte, il suffit de considérer la double décomposition suivante du nombre 4 en facteurs irréductibles :

$4 = 2\times 2 = (1 + \sqrt -3)(1- \sqrt -3)\;$

En revanche, l'anneau Z[(1 + $\sqrt -3$ )/2] composé des entiers d'Eisenstein est euclidien, comme le montre l'article sur la question.

Enfin, il existe une propriété fort utile sur les anneaux unitaires d'entiers quadratiques :

l'intersection d'un anneau unitaire d'entiers quadratiques et de Q est égale à Z.

Démonstrations

Le corps des fractions de l'anneau des entiers d'un corps quadratique Q[ $\sqrt d$ ] est isomorphe à Q[ $\sqrt d$ ].

Le plus petit corps contenant les entiers quadratiques de Q[ $\sqrt d$ ] contient 1 et $\sqrt d$ , il contient nécessairement Q[ $\sqrt d$ ]. Réciproquement Q[ $\sqrt d$ ] contient tous les éléments de l'anneau des entiers, ce qui montre que Q[ $\sqrt d$ ] est bien le plus petit corps contenant la fermeture intégrale. C'est donc, à un isomorphisme près, son corps des fractions.

Soit A un anneau unitaire contenant strictement Z et formé uniquement d'entiers quadratiques. Il existe un entier f, non carré parfait, tel que A est égal à Z[ω] ou ω est égal soit à $\sqrt f$ soit, si f est congru à 1 modulo 4, à (1 + $\sqrt f$ )/2.

On utilise pour cela le corps des fractions de A. Les démonstrations précédentes montrent que Q.A, c'est-à-dire l'ensemble des produits d'un rationnel par un élément de A est un corps, contenu dans son corps des fractions. Comme le corps des fractions est le plus petit contenant l'anneau, il est égal à Q.A. Ce qui montre l'existence d'un entier quadratique ω, de la forme de celle construite précédemment, tel que le corps des fractions de A soit égal à Q[ω]. Comme A est composé d'entiers quadratiques, A est un sous anneau de Z[ω] car Z[ω] contient tous les entiers quadratiques du corps. Il suffit de caractériser les sous-anneaux unitaires de Z[ω] pour démontrer cette proposition.

Supposons dans un premier temps qu'il existe un entier d sans facteur carré et non congru à 1 modulo 4 tel que ω soit égal à $\sqrt d$ et considérons l'ensemble E de tous les entiers strictement positifs n tel que n. $\sqrt d$ soit dans A. Montrons que cet ensemble est non vide, A n'est pas réduit à Z, il contient un élément de Z[ω] qui n'est pas un entier relatif. Soit a + b. $\sqrt d$ un tel entier, avec a et b inclus dans Z et b non nul. Comme tous les entiers de A sont éléments de Z[ω], un élément de A possède nécessairement une forme de cette nature. Comme Z est inclus dans A, -a est élément de A et -a + a + b. $\sqrt d$ = b. $\sqrt d$ est aussi élément de A. Et |b| est élément de E. E est un ensemble non vide d'entiers strictement positifs, il possède donc un élément minimal m.

On définit f comme égal à m².d. On remarque que $\sqrt f$ est un élément de A puisque soit m $\sqrt d$ soit -m $\sqrt d$ l'est (si -m $\sqrt d$ , alors m $\sqrt d$ l'est aussi par stabilité de la soustraction). Par conséquence Z[ $\sqrt f$ ] est inclus dans A. Montrons maintenant l'inclusion inverse. Soit a + b. $\sqrt d$ un élément quelconque de Z, une fois encore b. $\sqrt d$ est élément de A. considérons la division euclidienne de |b| par m, |b| = p.m + r. Comme |b|. $\sqrt d$ et p.m. $\sqrt d$ sont des éléments de A, par stabilité r. $\sqrt d$ l'est aussi. Or r est strictement plus petit que m, le fait que r. $\sqrt d$ soit élément de A montre que r est nul et b est un multiple de m. En conclusion a + b. $\sqrt d$ est bien un élément de Z[ $\sqrt f$ ]. On a montré que Z[ $\sqrt f$ ] contient A et est contenu dans A, ils sont donc égaux.

Supposons maintenant que ω = (1 + $\sqrt d$ )/d où d est congru à 1 modulo 4. Le raisonnement précédent s'applique encore et il existe un entier strictement positif m tel que A soit égal à Z[m/2(1 + $\sqrt d$ )]. Si m est paire, A est engengré par la somme d'un entier et de m $\sqrt d$ que l'on note toujours f, ce qui montre que A est égal à Z[ $\sqrt f$ ]. Supposons que m soit impair, alors A est engendré par (m - 1)/2 + (1 + $\sqrt f$ )/2 et donc par (1 + $\sqrt f$ )/2. Il ne reste plus qu'à monter que f est congru à 1 modulo 4. Dans ce dernier cas, m est impair, le carré de tout nombre impair est congru à 1 modulo 4, d l'est aussi, donc f égal à m².d est congru à 1 modulo 4, ce qui termine la démonstration.

l'intersection d'un anneau unitaire d'entiers quadratiques et de Q est égale à Z :

Dire que l'anneau est unitaire, signifie qu'il contient élément 1, par stabilité de l'addition et de la soustraction, il contient Z, réciproquement soit a un élément de l'intersection de l'anneau et de Q, comme il est élément de l'anneau, il est racine d'un polynôme de coefficient de monôme dominant égal à 1 et à coefficients dans Z. Ce polynôme admet pour racine a et son congugé est encore égal à a qui est donc une racine double, ont en déduit que son polynôme minimal est égal à X² - 2a.X + a². Ce qui montre que 2.a et a² sont des éléments de Z. Dire que 2.a est élément de Z revient à dire qu'il existe un entier b tel que a est égal à b/2. Dire que b²/4 est entier signifie que b est un multiple de 2, ce qui montre que a est entier.

Outils et théorèmes

Conjugué et norme

Article détaillé : Norme (arithmétique).

Deux applications sont ont un rôle privilégié dans les corps quadratiques.

L'application de Q[ $\sqrt d$ ] dans lui-même qui à au nombre a + b. $\sqrt d$ associe a - b. $\sqrt d$ est dite application conjuguée.

L'article Extension quadratique montre qu'il n'existe que deux automorphismes de corps. Un automorphisme est un morphisme bijectif et un morphisme désigne une application respectant la structure, ici les deux opérations d'addition et de multiplication. Un morphisme φ vérifie :

$\forall \alpha,\beta\in\Q[\sqrt d]\quad \varphi(\alpha + \beta) = \varphi(\alpha) + \varphi(\beta)\quad\text{et}\quad \varphi(\alpha \cdot \beta) = \varphi(\alpha) \cdot \varphi(\beta)$

Les deux automorphismes sont l'identité et l'application conjuguée. On remarque que si d est égal à -1, on retrouve le terme conjugué des nombres complexes.

La deuxième application importante est la suivante :

L'application de Q[ $\sqrt d$ ] dans Q qui à un nombre quadratique associe le produit de ce nombre par son conjugué est appelé norme.

Dans le reste de l'article, l'application norme est noté N. Dans le cas où d est égal à -1, on trouve le carré de la norme géométrique usuel. On peut se poser la question de savoir pourquoi les arithméticiens omettent d'ajouter la racine, à la différence des géomètres. La raison est la nature de l'ensemble d'arrivée de la fonction, il est égal à Q, ce qui n'est plus vrai avec la définition des géomètres. Cette propriété est essentielle pour de nombreux usages.

Si d est un entier positif, la norme n'a pas de raison d'être positive. La norme du nombre quadratique a + b. $\sqrt d$ est a² - d.b². Si d est égal à 2, a à 1 et b à 1, on trouve en effet -1.

L'application norme de Q[ $\sqrt$ d] respecte la multiplication :

$\forall \alpha,\beta\in\Q[\sqrt d]\quad \mathcal N(\alpha\cdot\beta) = \mathcal N(\alpha) \cdot\mathcal N(\beta)$

Cette propriété est une conséquence directe de la définition de la norme, si α et β désignent deux nombres quadratiques de Q[ $\sqrt d$ ], α' et β' leurs conjugués, alors :

$\mathcal N(\alpha\cdot\beta) = \alpha\beta\cdot \alpha'\beta' = \alpha\alpha'\cdot\beta\beta' = \mathcal N(\alpha) \cdot\mathcal N(\beta)$

La conjugaison est un automorphisme de l'anneau des entiers de Q[ $\sqrt$ d] et, sur cet ensemble, la norme est à valeurs dans Z.

On remarque que si α est un entier quadratique, son conjugué possède le même polynôme minimal, il est donc aussi entier quadratique. L'application conjuguée est injective sur A car elle l'est sur K. Comme l'application est involutive, c'est-à-dire que le conjugué du conjugué est l'élément initial, elle est nécessairement surjective. Puisque l'application conjugué est un morphisme dans K, il l'est nécessairement dans un sous-ensemble et a fortiori dans la fermeture intégrale. Soit α' le conjugué de α. On a déjà démontré que le produit de deux entiers quadratiques est encore un entier quadratique, on en déduit que α.α' est un entier quadratique élément de Q, il est donc élément de Z, d'après la proposition précédente.

Si ω est égal à $\sqrt d$ , la norme prend la forme (1), si d est congru à 1 modulo 4 et que ω est égal à (1 + $\sqrt d$ )/2 elle prend la forme (2) :

$\forall a,b\in\Z\quad \begin{align} (1)\quad d &\equiv 2\;\text{ou}\;3 &\mod 4 \quad &\mathcal N(a + b.\omega) = a^2 - d.b^2 \\ (2)\quad d &\equiv 1 &\mod 4 \quad &\mathcal N(a + b.\omega) = a^2 + ab - \frac {d-1}4b^2 \end{align}$

Groupe des unités

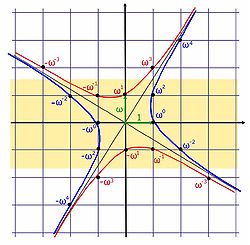Les éléments du groupe des unités se répartissent sur 4 branches d'hyperbole qui s'obtiennent à l'aide de rotations d'un quart de tour.

Article détaillé : Groupe des unités d'un anneau d'entiers quadratiques.

La première difficulté à résoudre pour comprendre la structure d'un anneau d'entiers quadratiques est son groupe des unités, c'est-à-dire le groupe formé par les éléments inversibles et munis de la multiplication. Une première remarque simplifie l'analyse, un entier quadratique est inversible si et seulement si sa norme est égale à ±1. Ce qui ramène la question à l'étude d'une des deux équations diophantienne x² - d.y² = ±1 ou si d est congru à 1 modulo 4 et si f désigne l'entier tel que d = 4f - 1 : x² + x.y - f.y² = ±1.

La première équation est étudiée^[5] depuis Diophante et porte le nom d'équation de Pell-Fermat. Elle est résolue de manière algorithmique par Bhāskara II^[6], un mathématicien indien du XII^e siècle, et par Joseph-Louis Lagrange en 1767 de manière théorique^[7], à l'aide des fractions continues.

Si d est strictement négatif, le groupe est réduit à ±1, sauf dans les cas où d est égal à -1, le groupe contient alors 4 éléments (cf l'article Entier de Gauss), ou si d est égal à -3 et il en contient 6. Si d est strictement positif, le groupe des unités contient une infinité de solutions. Plus précisément, il est isomorphe à Z/2Z x Z. Il existe une unique unité ρ dont les deux coordonnées sont positives et tel que toutes les autres s'expriment sous la forme e.ρ ^k où e est égal à ±1 et k un élément de Z. Il existe deux algorithmes célèbres et relativement efficaces pour trouver cette unité dite fondamentale.

Graphiquement si l'on représente l'anneau à l'aide du repère orthonormal (1, ω) les points de l'anneau se situent sur le quadrillage régulier contenant le point 0 et formé de carrés de côté 1. Les éléments du groupe des unités se trouvent sur 4 branches d'hyperboles qui s'obtiennent par rotations successives d'un quart de tour.

L'analyse du groupe des unités ne nécessite pas l'usage des propriétés de fermeture intégrale de l'anneau. En conséquence, les résultats sont encore vrais pour un anneau d'entiers quadratiques quelconque.

Décomposition en idéaux premiers

Article détaillé : Idéal de l'anneau des entiers d'un corps quadratique.

La deuxième obstruction est la conséquence des idéaux premiers mais non principaux. On a vu qu'ils induisent des décompositions multiples d'un entier quadratique en facteurs premiers. Deux théorèmes permettent encore de travailler malgré cette obstruction, ils ne s'appliquent que sur des fermetures intégrales, c'est-à-dire que l'anneau doit contenir tous les entiers quadratiques.

La manière d'analyser cette situation pour Ernst Kummer est de considérer qu'il manque des nombres irréductibles. Les idéaux premiers sont alors vus comme les nombres premiers manquants. L'objectif consiste à ne plus décomposer un nombre mais un idéal :

Tout idéal de l'anneau des entiers d'un corps quadratique Q[ω] se décompose de manière unique, à l'ordre près, en un produit d'idéaux premiers.

Pour étudier un tel anneau, il devient nécessaire d'expliciter les idéaux premiers. La majorité consiste en idéaux principaux et quelques autres ne le sont pas. Un deuxième théorème précise :

Il n'existe qu'un nombre fini d'idéaux premiers non principaux dans l'anneau des entiers d'un corps quadratique.

Le théorème de Stark-Heegner précise pour quels entiers d l'anneau est principal si d est négatif :

L'anneau des entiers du corps quadratique Q[ $\sqrt d$ ] pour les valeurs de d réduites et négatives est principal si, et seulement si, d est une des valeurs suivantes : −1, −2, −3, −7, −11, −19, −43, −67 ou −163^[8].

Dans le cas des entiers d positifs, les anneaux principaux sont beaucoup plus nombreux. En 2008, il est conjecturé qu'il en existe une infinité.

Applications

Classification des nombres premiers

Article détaillé : Décomposition des idéaux premiers.

La structure des entiers sur les corps quadratiques amène à étudier non pas les diviseurs d'un nombre premier p, mais les facteurs premiers de l'idéal pZ[u]. Cette analyse est utile pour la résolutions d'équations diophantiennes.

Nombre premier inerte

La première situation est celle où pZ[u] est un idéal premier :

On dit que p est inerte dans Z[u] si l'idéal principal engendré par p est premier.

Le nombre premier p est inerte si et seulement si -d n'est pas un résidu quadratique modulo p.

Le corps premier Z[u]/pZ[u] est isomorphe à F_p².

Démonstrations

Le nombre premier p est inerte si et seulement si -d n'est pas un résidu quadratique modulo p :

Le nombre premier p est inerte, si et seulement s'il n'existe pas de morphisme de Z[u] dans un le corps fini F_p à p élément. En effet, si un tel morphisme existe, son noyau est un idéal premier de norme p et si un idéal premier de norme p existe alors le morphisme de Z[u] dans le quotient remplit la condition.

Un tel morphisme existe si et seulement s'il est possible d'associer à $\sqrt d$ une valeur dans F_p, la seule valeur possible est une racine de l'équation X² = d, c'est-à-dire que d est résidu quadratique modulo p. Si tel est le cas, il existe une unique manière de prolonger l'application m qui à 1 associe 1 et à $\sqrt d$ une de ces deux racines quadratiques dans F_p. Comme l'idéal pZ[u] est premier un tel morphisme n'existe pas un tel morphisme n'existe pas et -d n'est pas un résidu quadratique modulo p.

Le corps premier Z[u]/pZ[u] est isomorphe à F_p² :

La norme de pZ[u] est égal à p². Si p est inerte, Z[u]/pZ[u] est un corps de cardinal la valeur absolue de norme de p, c'est-à-dire p². Il n'existe qu'un unique corps contenant p² éléments : F_p², ce qui permet de conclure.

Nombre premier décomposé

La deuxième situation est celle où pZ[u] n'est pas premier et contient dans sa décomposition deux idéaux premiers :

On dit que p est décomposé si son idéal principal contient deux idéaux premiers distincts.

Soit σ l'endomorphisme de Z[u] qui à 1 associe 1 et à $\sqrt d$ associe - $\sqrt d$ . Cette application est un morphisme d'anneau. L'application σ est dite conjugué. Dans le cas où d est négatif, elle se confond avec la fonction conjugué des nombres complexes.

Les deux idéaux sont conjugués l'un de l'autre et ce sont les seuls idéaux de norme p.

L'anneau quotient Z[u] / pZ[u] est isomorphe au produit F_pxF_p.

Démonstrations

Les deux idéaux sont conjugués l'un de l'autre et ce sont les seuls idéaux de norme p.

Remarquons tout d'abord que la norme de p est égal à p². Comme le produit des normes d'idéaux est égal à la norme du produit des idéaux et que le seul idéal de norme 1 est Z[u], la décomposition en idéal premier de pZ[u] ne peut contenir plus de deux idéaux distincts. Supposons qu'elle contienne exactement deux idéaux distincts M₁ et M₂.

Alors les normes de M₁ et M₂ sont égales à p et Z[u]/M_i, si i est égal à 1 ou à 2, est isomorphe au corps premier de cardinal p. Le paragraphe précédent montre qu'il existe un élément r du corps premier F^p tel que r² est égal à -d. Il existe exactement deux morphismes de corps de Z[u] dans F_p, ils associent à 1 la valeur 1 dans F_p et à $\sqrt d$ respectivement les valeurs r et -r. Les idéaux M₁ et M₂ sont les deux noyaux respectifs de ces deux morphismes. Ces deux morphismes sont conjugués, leurs noyaux le sont donc aussi.

L'anneau quotient Z[u] / pZ[u] est isomorphe au produit F_pxF_p :

Montrons que l'intersection de M₁ et M₂ est égal au produit M₁.M₂. Remarquons que le produit est nécessairement inclus dans l'intersection. Réciproquement soit m un élément de l'intersection. Comme ces deux idéaux sont maximaux et distincts, M₁ + M₂ est égal à Z[u], et 1 est la somme d'un élément de M₁ et d'un élément de M₂ : m₁ + m₂ = 1 et donc m.m₁ + m.m₂ = m, ce qui démontre l'égalité.

Le théorème chinois généralisé et le fait que Z[u] / M_i soit le corps à p éléments montrent que :

$\frac {\Z[u]}{p\Z[u]}=\frac{\Z[u]}{M_1\cdot M_2}=\frac{\Z[u]}{M_1 \cap M_2}=\frac {\Z[u]}{M_1}\times\frac{\Z[u]}{M_2}=\mathbb F_p\times\mathbb F_p$

Nombre premier ramifié

Il se peut que pZ[u] ne soit contenu que dans un unique idéal premier :

On dit que p est ramifié s'il existe un unique idéal premier M contenant p et que pZ[u] n'est pas premier.

Si ce cas se produit, alors

Si le nombre premier p est ramifié, l'idéal pZ[u] est égal au carré de l'unique idéal premier contenant p.

Le nombre premier p est ramifié, si et seulement s'il divise le discriminant de l'anneau Z[u].

L'anneau quotient Z[u] / pZ[u] est de cardinal p² et contient au moins un élément nilpotent, non nul.

Démonstrations

Si le nombre premier p est ramifié, l'idéal pZ[u] est égal au carré de l'unique idéal M premier contenant p :

Il a déjà été démontré que la décomposition de pZ[u] est le produit d'un ou deux idéaux premiers. Si p n'est pas premier, alors pZ[u] est un produit de deux idéaux premiers. Comme il n'en existe qu'un, noté M, contenant l'idéal pZ[u], il est nécessairement égal à M².

L'anneau quotient Z[u] / pZ[u] contient au moins un élément nilpotent :

M contient un élément qui n'est pas multiple de p car, par hypothèse M n'est pas égal à l'idéal engendré par p. Soit α la classe de cet élément dans Z[u] / pZ[u]. Comme le carré de M est égal à pZ[u], α² est nul. L'élément α n'est pas nul dans Z[u] / pZ[u] car il contient un représentant qui n'est pas dans M, en revanche son carré l'est. Ce qui montre que l'anneau quotient contient au moins un élément nilpotent.

Le nombre premier p est ramifié, si et seulement s'il divise le discriminant de l'anneau Z[u].

Supposons que p soit ramifié, le quotient de Z[u] par pZ[u] est un F_p espace vectoriel. Il contient un élément non nul α nilpotent d'ordre deux. L'élément α n'est pas colinéaire à la classe de 1 car aucun multiple de 1 n'est nilpotent, (1, α) forme donc une base de l'espace vectoriel quotient. Soit x et y deux vecteurs de coordonnées (x₁, x₂) et (y₁, y₂) dans la base (1, α). La matrice Μ_xy de l'homothétie de rapport xy est la suivante :

$\Mu_{xy} = \begin{pmatrix} x_1y_1 & 0 \\ x_1y_2 +x_2y_1 & x_1y_1 \end{pmatrix}$

On en déduit la forme trace et la matrice T associée :

$\text{Tr}\langle x,y\rangle = 2x_1y_1\quad \text{et}\quad T = \begin{pmatrix} 2 & 0 \\ 0 & 0 \end{pmatrix}$

Le déterminant de T est ainsi nul. Ce déterminant est le quotient dans Z/pZ du discriminant de l'anneau Z[u]. On en déduit que le discriminant est un multiple de p, ce qu'il fallait démontrer.

Réciproquement, si p n'est pas un diviseur du discriminant, le déterminant de T dans le quotient Z[u] / pZ[u] est, à un facteur multiplicatif près, la classe du discriminant de Z[u] dans Z/pZ qui n'est pas nul. En conséquence, il n'existe pas d'élément nilpotent, ce qui montre que p ne peut être ramifié.

Équation diophantienne

La raison initiale du développement des corps quadratiques est l'étude d'équations diophantiennes d'ordre deux. Illustrons par deux exemples comment la théorie précédente permet de venir à bout de questions de cette nature.

x² + 2.y² = p

Le cas d égal à -1 ou à -3 est traité dans l'article théorème des deux carrés de Fermat. Ici, d est égal à -2 :

$p = x^2 + 2y^2 \Leftrightarrow p\equiv 1\mbox{ ou }p\equiv 3\pmod{8}$

En effet, calcul analogue à celui présenté pour les entiers de Gauss montre que l'anneau est euclidien donc principal. S'il existe un idéal contenant p éléments, comme il est principal et que sa norme est égale à p, le tour est joué. Cette méthode s'applique à tous les anneaux d'entiers euclidiens.

Détails de la démonstration

Dans un premier temps déterminons les valeurs de p tel que -2 est un résidu quadratique. L'article Loi de réciprocité quadratique montre que -1 est un carré si et seulement si p est congru à 1 modulo 4. La valeur 2 est un carré si et seulement si p est congru à 1 ou à 7 modulo 8. On obtient le tableau suivant :

modulo	1	3	5	7
-1	+	-	+	-
2	+	-	-	+
-2	+	+	-	-

Le signe + signifie que la valeur est un carré pour un nombre premier congru à la valeur de la première ligne modulo 8. On en conclut que -2 est un carré modulo p si et seulement si p est congru à 1 ou à 3.

Si cette condition n'est pas remplie, il est impossible de construire un morphisme de Z[i $\sqrt 2$ ] dans Z/pZ, ce qui montre que p est inerte et qu'il n'y a pas de solution.

Si p est congru à 1 ou à 3 modulo 8, il existe dans Z/pZ une valeur r de carré égal à -2. L'application qui à l'entier algébrique a + b.i $\sqrt 2$ associe a + b.r dans Z/pZ est un morphisme d'anneau. Son noyau est un idéal de Z[i $\sqrt 2$ ]. Comme l'anneau est euclidien, l'idéal est principal, soit α + β.i $\sqrt 2$ un générateur. La norme de ce générateur est égal au cardinal de l'anneau quotient, en l'occurrence p. La norme de l'idéal est aussi la valeur absolue de la norme d'un générateur. Elle est égale à α² + 2.β² et à p. Ce qui résout l'équation.

x² + 5.y² = p

Si d est égal à 5, la situation est plus délicate car l'anneau Z[i $\sqrt 5$ ] n'est pas euclidien, elle se résume de la manière suivante :

$p = x^2 + 5y^2 \Leftrightarrow p\equiv 1\mbox{ or }p\equiv 9\pmod{20},$ $2p = x^2 + 5y^2 \Leftrightarrow p\equiv 3\mbox{ or }p\equiv 7\pmod{20}.$

Si initialement la méthode est la même que pour le cas euclidien, il devient nécessaire d'établir la nature des idéaux de norme p. S'il est principal, une solution existe, sinon la valeur p n'est pas atteinte par la fonction. Le groupe des classes permet de s'en rendre compte. Cette méthode est générale, cependant pour des valeurs importantes de d les calculs s'avèrent fastidieux.

Détail de la démonstration

Dans un premier temps recherchons les nombres premiers inertes. L'application de la loi de réciprocité quadratique montre que 5 est un résidu quadratique modulo p si et seulement si p est un résidu quadratique modulo 5. Or Z/5Z contient deux classes de résidus, celle de 1 et celle de 4. On en déduit le tableau suivant, construit comme précédemment :

modulo	1	3	7	9	11	13	17	19
-1	+	-	-	+	-	+	+	-
5	+	-	-	+	+	-	-	+
-5	+	+	+	+	-	-	-	-

Un raisonnement analogue au précédent montre que les classes de 11, 13, 17 et 19 sont inertes.

Il reste quatre classes ramifiées ou décomposées. Il s'agit de déterminer si les idéaux associés sont principaux ou non. Pour cela examinons le groupe des classes de l'anneau. Un résultat établi précédemment montre que toute classe contient un idéal de norme inférieure à 4. $\sqrt 5$ / π. Comme la norme est un entier relatif, la seule valeur possible pour un représentant d'une classe différente de celle des idéaux principaux est 2. On vérifie qu'un unique idéal : M₂ contenant 2 et 1 + i. $\sqrt 5$ est de norme 2. Il n'est pas principal car aucun élément de l'anneau n'a pour norme en valeur absolue 2.

Le groupe des classes de l'anneau d'entiers algébriques Z[i $\sqrt 5$ ] est d'ordre 2.

Le discriminant de Z[i $\sqrt 5$ ] est égal à -20, l'idéal M₂ est ramifié et l'anneau quotient Z[i $\sqrt 5$ ] / M₂ contient des éléments nilpotents comme 1 + i. $\sqrt 5$ , dont le carré est multiple de 2.

L'existence d'un idéal premier non principal de norme 2 amène à étudier la parité des solutions de l'équation. Soit a et b deux entiers relatifs premiers entre eux tel que a² + 5.b² soit un multiple de p. Si la somme est paire, les entiers a et b sont impairs et donc congru à 1 ou à 3 modulo 4. Leur carré est congru à 1 modulo 8, en conséquence a² + 5.b² est congru à 6 modulo 8 et p est congru à 3 modulo 4. Dans ce cas là, p est congru à 3 ou 7 modulo 20. Si la somme est impaire, l'un des deux nombres est pair et l'autre impair, le carré de celui impair est congru à 1 modulo 4 et l'autre est un multiple de quatre. La somme est donc congru à 1 modulo 4 et p est congru à 1 ou 9 modulo 20.

Si p est congru à 3 ou à 7 modulo 20, l'équation ne peut admettre de solution égale à p car toute solution est paire. En conséquence, aucun idéal M_p de norme p ne peut être principal, il serait en effet généré par une solution de l'équation. En revanche, l'idéal M₂.M_p l'est car le groupe des classes est d'ordre deux et M₂ n'est pas principal. L'idéal M₂.M_p est de norme 2.p, il contient un générateur et sa norme est égal à 2.p, ce qui revient à dire que si p est congru à 3 ou 7 modulo 20, l'équation x² + 5.y² = 2.p admet une solution.

Si p est congru à 1 ou à 9 modulo 20, l'équation x² + 5.y² = 2p ne peut admettre de solution. Le raisonnement précédent montre que M₂.M_p ne peut être principal et donc M_p l'est, ce qui permet de conclure.

Classification des formes quadratiques

Voir Principe local-global.

Notes et références

Notes

↑ (en) John Stillwell (en), Mathematics and its History, Springer, 3^e éd., 2010 (ISBN 978-1-44196052-8), p. 75-77
↑ Fermat termine son défi par : « J'attends la solution de ces questions ; si elle n'est fournie ni par l'Angleterre, ni par la Gaule Belgique ou Celtique, elle le sera par la Narbonnaise » (Laurent Hua et Jean Rousseau, Fermat a-t-il démontré son grand théorème ? l'hypothèse "Pascal", L'Harmattan, 2002 (ISBN 978-2-74752836-8), p. 113).
↑ Par exemple Bas Edixhoven (de) et Laurent Moret-Bailly, Théorie algébrique des nombres, cours de maîtrise de mathématiques, université de Rennes I, 2004 [lire en ligne] .
↑ Ne pas confondre avec la fermeture algébrique, ou clôture algébrique.
↑ (en) Leonard Eugene Dickson, History of the Theory of Numbers [détail des éditions], vol. 2
↑ Bhāskara II, Bijaganita (1150), cf (en) John J. O’Connor et Edmund F. Robertson, « Pell's equation », dans MacTutor History of Mathematics archive, université de St Andrews [lire en ligne] ..
↑ J.-L. Lagrange, Solution d'un problème d'arithmétique
↑ La démonstration est technique, on la trouve par exemple sur le site The Gauss class number problem for imaginary quadratic fields par G. Goldfeld

Références

(en) David A. Cox, Primes of the Form x²+ny², Wiley, 1997 (1^re éd. 1989) (ISBN 978-0-47119079-0)
(en) G. H. Hardy et E. M. Wright (en), An Introduction to the Theory of Numbers [détail des éditions]
(en) Kenneth Ireland et Michael Rosen (de), A Classical Introduction to Modern Number Theory, Springer, 1990 (réimpr. 1998), 2^e éd. (ISBN 978-0-38797329-6)
Pierre Samuel, Théorie algébrique des nombres [détail des éditions]
Jean-Pierre Serre, Cours d'arithmétique [détail des éditions]

Lien externe

(en) Eric W. Weisstein, « Quadratic Field », MathWorld

Portail des mathématiques

Catégorie :

Entier quadratique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Entier quadratique de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

Entier De Dirichlet — Pour les articles homonymes, voir Entier (homonymie). Dirichlet En mathématiques, et plus précisément en arithmétique modulai … Wikipédia en Français
Entier de dirichlet — Pour les articles homonymes, voir Entier (homonymie). Dirichlet En mathématiques, et plus précisément en arithmétique modulai … Wikipédia en Français
Entier Algébrique — Pour les articles homonymes, voir Entier (homonymie). En mathématiques, les entiers algébriques forment une famille de nombres qui généralise l ensemble des nombres entiers dits relatifs. Ils jouent un rôle analogue à ces derniers en théorie… … Wikipédia en Français
Entier algebrique — Entier algébrique Pour les articles homonymes, voir Entier (homonymie). En mathématiques, les entiers algébriques forment une famille de nombres qui généralise l ensemble des nombres entiers dits relatifs. Ils jouent un rôle analogue à ces… … Wikipédia en Français
Entier De Gauss — Pour les articles homonymes, voir Entier (homonymie). Carl Friedrich Gauss. En mathématiques, et plus précisément en … Wikipédia en Français
Entier de gauss — Pour les articles homonymes, voir Entier (homonymie). Carl Friedrich Gauss. En mathématiques, et plus précisément en … Wikipédia en Français
Entier de Dirichlet — Pour les articles homonymes, voir Entier (homonymie). Dirichlet En mathématiques, et plus précisément en arithmétique modulaire, nous appellerons … Wikipédia en Français
Entier algébrique — Pour les articles homonymes, voir Entier (homonymie). En mathématiques, les entiers algébriques forment une famille de nombres qui généralise l ensemble des nombres entiers dits relatifs. Ils jouent un rôle analogue à ces derniers en théorie… … Wikipédia en Français
Entier de Gauss — Pour les articles homonymes, voir Entier (homonymie). Carl Friedrich Gauss. En mathématiques, et plus précisément en théorie algébrique des nombres, un entier de … Wikipédia en Français
Entier d'Eisenstein — Les entiers d Eisenstein sont les points d intersection d un treillis triangulaire dans le plan complexe En mathématiques, les entiers d Eisenstein, nommés en l honneur du mathématicien Gotthold Eisenstein, sont des nombres complexes de la forme … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Entier quadratique

Sommaire

Préambule

Motivation

Anneaux euclidiens

Groupe des unités

Anneaux non factoriels

Caractérisation

Irrationnel quadratique

Corps quadratique

Entier quadratique

Fermeture intégrale et clôture intégrale

Outils et théorèmes

Conjugué et norme

Groupe des unités

Décomposition en idéaux premiers

Applications

Classification des nombres premiers

Nombre premier inerte

Nombre premier décomposé

Nombre premier ramifié

Équation diophantienne

x² + 2.y² = p

x² + 5.y² = p

Classification des formes quadratiques

Notes et références

Notes

Références

Lien externe

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Entier quadratique

Sommaire

Préambule

Motivation

Anneaux euclidiens

Groupe des unités

Anneaux non factoriels

Caractérisation

Irrationnel quadratique

Corps quadratique

Entier quadratique

Fermeture intégrale et clôture intégrale

Outils et théorèmes

Conjugué et norme

Groupe des unités

Décomposition en idéaux premiers

Applications

Classification des nombres premiers

Nombre premier inerte

Nombre premier décomposé

Nombre premier ramifié

Équation diophantienne

x2 + 2.y2 = p

x2 + 5.y2 = p

Classification des formes quadratiques

Notes et références

Notes

Références

Lien externe

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link

x² + 2.y² = p

x² + 5.y² = p