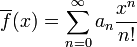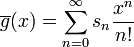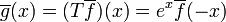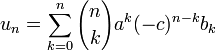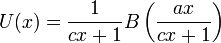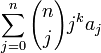- Transformation d'Euler
-
Transformation binomiale
En mathématiques, dans le domaine de l'analyse combinatoire, la transformation binomiale est une suite d'opérations transformant une suite en une autre, en calculant les différences entre les termes consécutifs.
Cette transformation est en rapport avec la transformation d'Euler , qui est le résultat d'une transformation binomiale à une suite associée à une fonction génératrice usuelle. Un cas particulier de la transformation d'Euler est parfois utilisé pour accélérer la convergence de séries alternées (voir l'accélération des séries). Un autre cas particulier apparaît dans une application aux séries hypergéométriques.
Sommaire
Définition
La transformation binomiale, T, d'une suite, (an), est la suite (sn) définie par
Formellement, nous pouvons écrire (Ta)n = sn pour représenter la transformation, où T est un opérateur en dimension infinie dont la matrice a pour coefficients Tnk vérifiant:
Cette transformation est une involution, c'est-à-dire
ou, en utilisant des notations indicielles:
où δ est le symbole de Kronecker. La suite de départ peut ainsi être retrouvée par
La transformation binomiale d'une suite est justement la nème différence de la suite, et ainsi
- s0 = a0
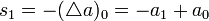
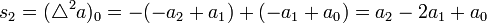
- . . .
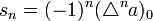
où Δ est l'opérateur de différence.
Certains auteurs définissent la transformation binomiale avec un signe additionnel, qui empêche la transformation d'être involutive:
dont la transformation réciproque est
Décalages
La transformation binomiale correspond à l'opérateur de translation à droite pour la suite des nombres de Bell. c'est-à-dire:
où les Bn représentent les nombres de Bell.
Fonctions génératrices ordinaires
La transformation relie les fonctions génératrices associées à des séries.
Pour des fonctions génératrices ordinaires
et
on a
Transformation d'Euler
La transformation correspondante reliant les fonctions génératrices ordinaires est appelée transformation d'Euler. Elle apparaît couramment sous une ou deux formes, l'une étant utilisée pour l'accélération de la convergence des séries alternées.
Cette forme intervient avec la relation:
obtenue en remplacent x = 1 / 2 dans la relation précédente. Les termes dans le membre de droite deviennent généralement petit, beaucoup plus vite, permettant ainsi un calcul numérique rapide de la somme.
La transformation d'Euler est aussi fréquemment appliquée aux séries hypergéométriques
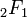 . Dans ce cas, la transformation d'Euler prend la forme de:
. Dans ce cas, la transformation d'Euler prend la forme de:La transformation binomiale, et ses variantes comme la transformation d'Euler, est connue pour son utilisation avec les fractions continues représentant un nombre. Soit 0 < x < 1 un réel ayant la représentation sous forme de fraction continue suivante:
Alors
et
Fonction génératrice exponentielle
Considérons des fonctions génératrices exponentielles,
et
Alors
La transformation de Borel convertit les fonctions génératrices ordinaires en fonctions génératrices exponentielles.
Représentation intégrale
Lorsque la suite peut être interpolée par une fonction analytique complexe, alors la transformation binomiale de la suite peut être représentée par la moyenne d'une intégrale de Nörlund-Rice sur la fonction d'interpolation.
Généralisations
Prodinger donna une transformation de type modulaire:
donne
où U et B sont des fonctions génératrices ordinaires associées aux séries:
{un} et {bn}, respectivement.
La k-transformation binomiale montante est parfois définie paret la k-transformation binomiale descendante , par
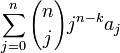 .
.
Les deux transformations sont des homomorphismes du noyau de la transformation de Hankel d'une série.
Voir aussi
- Série de Newton
- Matrice de Hankel
- Transformation de Möbius
- Transformation de Stirling
Références
- Donald E. Knuth, The Art of Computer Programming Vol. 3, (1973) Addison-Wesley, Reading, MA. (en)
- Helmut Prodinger, Some information about the Binomial transform, (1992) (en)
- Michael Z. Spivey and Laura L. Steil, The k-Binomial Transforms and the Hankel Transform, (2006) (en)
- Portail des mathématiques
Catégorie : Analyse combinatoire
Wikimedia Foundation. 2010.

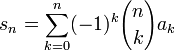
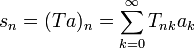
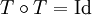
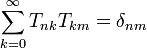
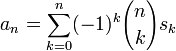
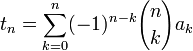
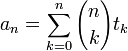
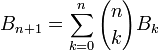
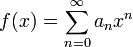
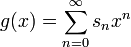
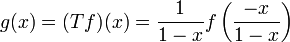
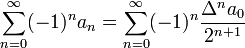
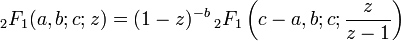
![x=[0;a_1, a_2, a_3,\cdots]](/pictures/frwiki/53/5bade4280d3a9f547e620492527584ca.png)
![\frac{x}{1-x}=[0;a_1-1, a_2, a_3,\cdots]](/pictures/frwiki/55/77d54d68045c9eedeb2cab19b382af3f.png)
![\frac{x}{1+x}=[0;a_1+1, a_2, a_3,\cdots]](/pictures/frwiki/98/b2e6db237aac5632aedc87e24d7a7d01.png)