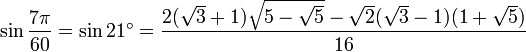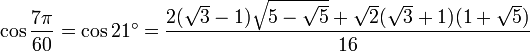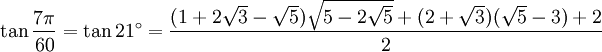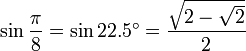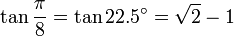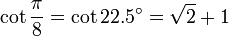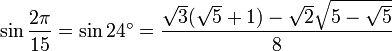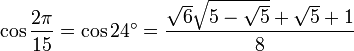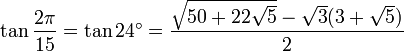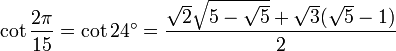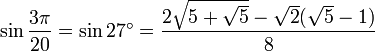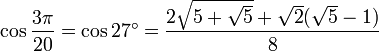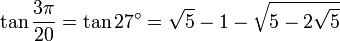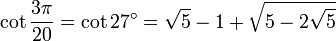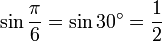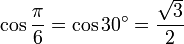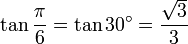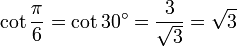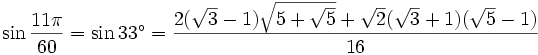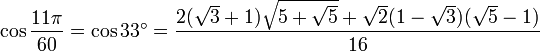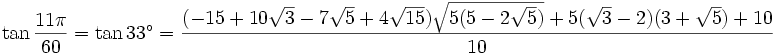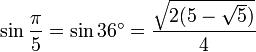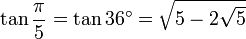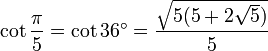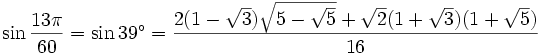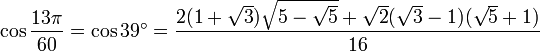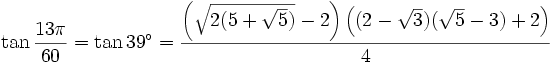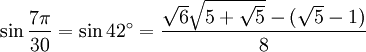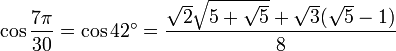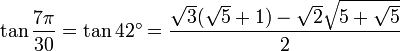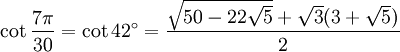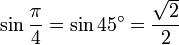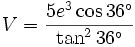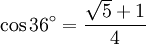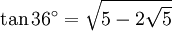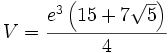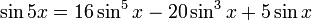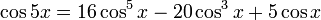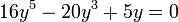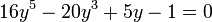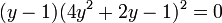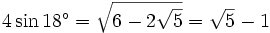- Constante trigonometrique exacte
-
Constante trigonométrique exacte
En mathématiques, les expressions de constantes exactes pour les expressions trigonométriques sont parfois très utiles, principalement pour la simplification des solutions en radicaux qui permettent des simplifications supplémentaires.
Toutes les valeurs de sinus, cosinus et tangente d'angles d'incrément de 3° sont dérivables en utilisant les identités : demi-angle, Double-angle, Addition/soustraction ainsi que les valeurs pour 0°, 30°, 36° et 45°. Note : 1°
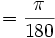 radians.
radians.Cet article est incomplet dans au moins deux sens. D'abord, il est toujours possible d'appliquer la formule du demi-angle et trouver une expression exacte pour le cosinus d'un demi du plus petit angle de la liste. Ensuite, cet article exploite seulement les deux premiers des cinq nombres premiers de Fermat connu : 3 et 5. On pouvait en principe noter des formules impliquant les angles
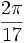 ,
, 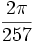 , ou
, ou 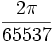 , mais elles auraient été trop difficiles à manier pour la plupart des applications. En pratique, toutes les valeurs de sinus, cosinus et tangente absentes dans cet article sont approximées en utilisant les techniques décrites dans l'article Construire des tables trigonométriques.
, mais elles auraient été trop difficiles à manier pour la plupart des applications. En pratique, toutes les valeurs de sinus, cosinus et tangente absentes dans cet article sont approximées en utilisant les techniques décrites dans l'article Construire des tables trigonométriques.Table des constantes
Les valeurs en dehors des angles 0° ... 45° sont trivialement extraites des axes du cercle unité par réflexion symétrie à partir de ces valeurs. (Voir Identité trigonométrique)
0° Fondamental
3° - Polygone à 60 côtés
6° - Polygone à 30 côtés
9° - Polygone à 20 côtés
12° - Polygone à 15 côtés
15° - Polygone à 12 côtés
18° - Polygone à 10 côtés
20° - Ennéagone
21° - Somme 9° + 12°
22,5° - Octogone
24° - Somme 12° + 12°
27° - Somme 12° + 15°
30° - Hexagone
33° - Somme 15° + 18°
36° - Pentagone
39° - Somme 18°+ 21°
42° - Somme 21° + 21°
45° - Carré
Notes
Usages des constantes
Pour un exemple de l'usage de ces constantes, considérons un dodécaèdre avec le volume suivant, où e est la longueur de l'arête :
En utilisant
ceci peut être simplifié en :
Triangles de dérivation
 Polygone régulier (à N cotés) et son triangle droit fondamental. Angle : a = 180/N °
Polygone régulier (à N cotés) et son triangle droit fondamental. Angle : a = 180/N °
La dérivation des constantes de sinus, cosinus et tangente sous formes radiales est basée sur la constructabilité des triangles droits.
Ici se trouvent des triangles droits faits à partir de sections symétriques de polygones réguliers qui sont utilisés pour calculer les rapports trigonométriques fondamentaux. Chaque triangle droit représente trois points dans un polygone régulier : un sommet, un centre d'arête contenant ce sommet et le centre du polygone. Un N-gone peut être divisé en 2N triangles droits avec des angles de
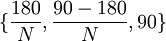 degrés, pour N = 3, 4, 5, ...
degrés, pour N = 3, 4, 5, ...La constructibilité des polygones à 3, 4, 5 et 15 côtés est la base et les bissectrices des angles permettent les multiples de deux qui sont ainsi dérivés.
- Constructible
- Polygones réguliers à
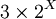 côtés, X = 0, 1, 2, 3, ...
côtés, X = 0, 1, 2, 3, ...
- Triangle 30°-60°-90° - triangle (3 côtés)
- Triangle 60°-30°-90° - hexagone (6 côtés)
- Triangle 75°-15°-90° - dodécagone (12 côtés)
- Triangle 82,5°-7,5°-90° - icosikaitétragone (24 côtés)
- Triangle 86,25°-3,75°-90° - tétracontakaioctagone (48 côtés)
- ...
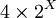 côtés
côtés
- Triangle 45°-45°-90° - carré (4 côtés)
- Triangle 67,5°-22,5°-90° - octogone (8 côtés)
- Triangle 88,75°-11,25°-90° - hexakaidécagone (16 côtés)
- ...
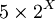 côtés
côtés
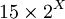 côtés
côtés
- Triangle 78°-12°-90° - pentakaidécagone (15 côtés)
- Triangle 84°-6°-90° - tricontagone (30 côtés)
- Triangle 87°-3°-90° - hexacontagone (60 côtés)
- Triangle 88,5°-1,5°-90° - hectoicosagone (120 côtés)
- Triangle 89,25°-0,75°-90° - dihectotétracontagone (240 côtés)
- ... (les polygones réguliers constructibles plus hauts ne donnent pas des angles de degrés entiers : 17, 51, 85, 255, 257...)
- Polygones réguliers à
- Non constructibles (avec des angles en degrés entiers ou moitié) - Aucune expression radicale finie impliquant les nombres réels pour ces rapports de bords de triangle n'est possible à cause des Casus Irreducibilis.
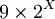 côtés
côtés
- Triangle 70°-20°-90° - ennéagone (9 côtés)
- Triangle 80°-10°-90° - octakaidécagone (18 côtés)
- Triangle 85°-5°-90° - triacontakaihexagone (36 côtés)
- Triangle 87,5°-2,5°-90° - heptacontakaidigone (72 côtés)
- ...
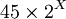 côtés
côtés
- Triangle 86°-4°-90° - tétracontakaipentagone (45 côtés)
- Triangle 88°-2°-90° - ennéacontagone (90 côtés)
- Triangle 89°-1°-90° - hectaoctacontagone (180 côtés)
- Triangle 89,5°-0,5°-90° - trihectohexacontagone (360 côtés)
- ...
Comment les valeurs trigonométriques pour sin et cos ont-elles été calculées ?
Les triviales
- Dans le format des degrés : 0, 90, 45, 30 et 60 peuvent être calculés à partir de leurs triangles, en utilisant le théorème de Pythagore.
n π sur 10
- Les formules des multiples d'angle pour les fonctions de 5x, où x = {18, 36, 54, 72, 90} et 5x = {90, 180, 270, 360, 540}, peuvent être résolues pour les fonctions de x, puisque nous connaissons les valeurs des fonctions de 5x. Les formules de multiples d'angles sont :
- Lorsque sin 5x = 0 ou cos 5x = 0, alors nous posons y = sin x ou y = cos x et résolvons pour y :
-
- Une solution est zéro, et l'équation du 4e degré résultante peut être résolue comme une équation quadratique dont y est élevé au carré.
- Lorsque sin 5x = 1 ou cos 5x = 1, nous posons de nouveau y = sin x ou y = cos x et nous résolvons pour y :
-
- qui se factorise en
n π sur 20
- 9° c'est 45 - 36 et 27° c'est 45 - 18 ; donc nous utilisons les formules de soustraction pour sin et cos.
n π sur 30
- 6° c'est 36 - 30, 12° c'est 30 - 18, 24° c'est 54 - 30 et 42° c'est 60 - 18 ; donc nous utilisons les formules de soustraction pour sin et cos.
n π sur 60
- 3° c'est 18 - 15, 21° c'est 36 - 15, 33° c'est 18 + 15 et 39° c'est 54 - 15, donc nous utilisons les formules de soustraction (ou d'addition) pour sin et cos.
Comment les valeurs trigonométriques pour tan et cot ont-elles été calculées ?
- La tangente est le sinus divisé par le cosinus, et la cotangente est le cosinus divisé par le sinus.
- Former chaque fraction et simplifier.
Plans pour la simplification
Rationaliser le dénominateur
- Si le dénominateur est une racine carrée, multiplier le numérateur et le dénominateur par ce radical.
- Si le dénominateur est la somme ou la différence de deux termes, multiplier le numérateur et le dénominateur par le conjugué du dénominateur. Le conjugué est identique, excepté le signe entre les termes qui est changé.
Séparer une fraction en deux
- Quelquefois, séparer la fraction en somme de deux fractions, puis les simplifier séparément peut aider.
Élever au carré et racine carrée
- S'il existe un terme compliqué, avec seulement une sorte de radical dans un terme, ce plan peut aider. Élever au carré le terme, combiner les termes qui se ressemblent et prendre la racine carrée. Ceci peut enlever un gros radical avec un radical plus petit à l'intérieur, mais il est souvent meilleur que l'original.
Simplification des expressions radicales imbriquées
Article détaillé : radical imbriqué.En général, les radicaux imbriqués ne peuvent pas être réduits.
Mais si pour
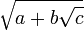 ,
,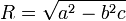 est rationnel,
est rationnel,
et pour les deux
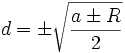 et
et 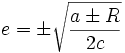 sont rationnels,
sont rationnels,avec le choix approprié pour les quatre signes
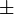 ,
,Alors
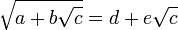
Exemple :
Voir aussi
- Fonction trigonométrique
- Identité trigonométrique
- Polygone constructible
Liens externes
- Portail des mathématiques
Catégories : Trigonométrie | Algèbre
Wikimedia Foundation. 2010.

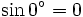
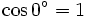
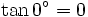
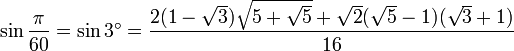
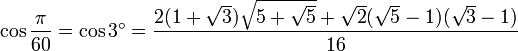
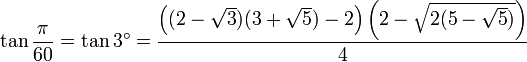
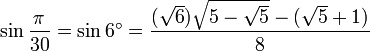
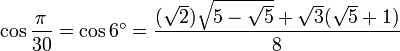
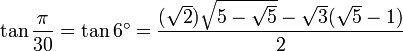
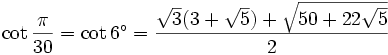
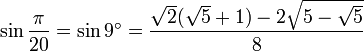
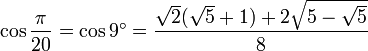
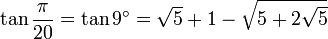
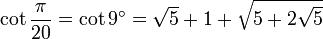
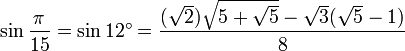
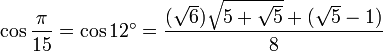
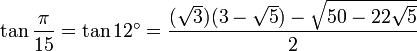
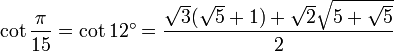
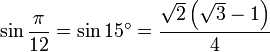
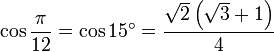
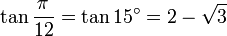
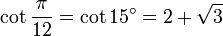
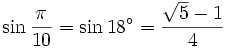
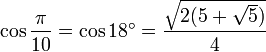
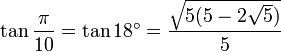
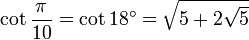
![\sin\frac{\pi}{9}=\sin 20^\circ=\sqrt[3]{-\frac{\sqrt{3}}{16}+\sqrt{-\frac{1}{256}}}+\sqrt[3]{-\frac{\sqrt{3}}{16}-\sqrt{-\frac{1}{256}}}=](/pictures/frwiki/100/dd7a789509b10ee48572e78001945c59.png)
![2^{-\frac{4}{3}}(\sqrt[3]{i-\sqrt{3}}-\sqrt[3]{i+\sqrt{3}})](/pictures/frwiki/54/6ff772b9ee1f07ad040d53e6a2eabb2d.png)
![2^{-\frac{4}{3}}(\sqrt[3]{1+i\sqrt{3}}+\sqrt[3]{1-i\sqrt{3}})](/pictures/frwiki/56/81c0f68771bc1866314e3aea2e60fe57.png)