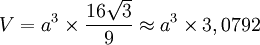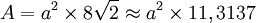- Dodécaèdre Rhombique
-
Dodécaèdre rhombique
Dodécaèdre rhombique 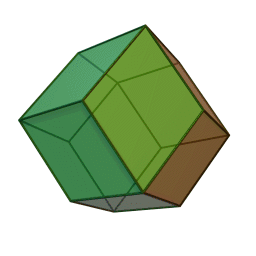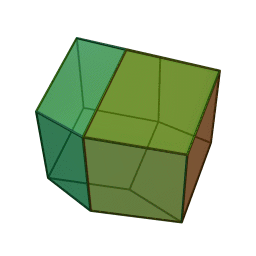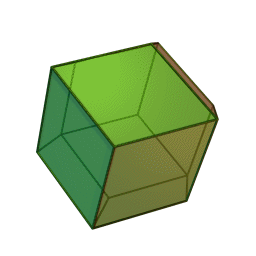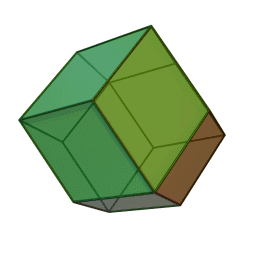
Type Solide de Catalan Faces Losanges Éléments :
· Faces
· Arêtes
· Sommets
· Caractéristique
12
24
14
2Faces par sommet 3 et 4 Sommets par face 4 Isométries Octaédrique Dual Cuboctaèdre Propriétés {{{propriétés}}} Le dodécaèdre rhombique est un polyèdre convexe à 12 faces rhombiques. C'est un solide dual d'un solide d'Archimède ou un solide de Catalan. Son dual est le cuboctaèdre.
Sommaire
Propriétés
C'est le polyèdre dual du cuboctaèdre et un zonoèdre. La grande diagonale de chaque face est exactement √2 fois la longueur de la petite diagonale, ainsi, les angles aigus de chaque face mesurent 2 tan-1(1/√2), ou approximativement 70,53°.
Étant le dual d'un solide d'Archimède, le dodécaèdre rhombique est de faces uniformes, ce qui signifie que le groupe de symétrie du solide agit transitivement sur l'ensemble des faces. En termes élémentaires, ceci signifie que pour deux faces quelconques A et B, il existe une rotation ou une réflexion du solide qui le laisse occuper la même région de l'espace en déplaçant la face A vers la face B.
Le dodécaèdre rhombique est un des neuf polyèdres convexes à faces uniformes, les autres étant les cinq solides de Platon, le cuboctaèdre, l'icosidodécaèdre et le triacontaèdre rhombique.
Le dodécaèdre rhombique peut être utilisé pour paver un espace à trois dimensions. Il peut être empilé pour remplir un espace comme les hexagones remplissent le plan; les cellules dans un réseau ont une forme similaire au dodécaèdre rhombique coupé par la moitié.
Ce pavage peut être vu comme le diagramme de Voronoï d'un réseau cubique à face centrées. Les abeilles utilisent la géométrie des dodécaèdres rhombiques pour former leurs nids d'abeille à partir du pavage des cellules, chacune d'elle est un prisme hexagonal couvert avec la moitié d'un dodécaèdre rhombique.
Le dodécaèdre rhombique forme la coque de la première projection par sommets d'un tesseract vers les 3 dimensions. Il existe exactement deux manières de décomposer un dodécaèdre rhombique en quatre parallélépipèdes congruents, ce qui donne 8 parallélépipèdes possibles. Les 8 cellules du tesseract sous cette projection sont précisément ces 8 parallélépipèdes.
Coordonnées cartésiennes
Les huit somment où trois faces se rencontrent sur leur angles obtus ont pour coordonnées cartésiennes
- (±1, ±1, ±1)
Les six sommets où les quatre faces se rencontrent sur leurs angles aigus sont donnés par les permutations de
- (0, 0, ±2)
Mesures et volume
Si son arête est a, son volume vaut :
Sa surface est de :
Bibliographie
- Robert Williams, The Geometrical Foundation of Natural Structure: A Source Book of Design, 1979, ISBN 0-486-23729-X
Voir aussi
Articles connexes
Liens externes
- (en) Dodécaèdre rhombique sur le site MathWorld
- (en) Les polyèdres en réalité virtuelle L'encyclopédie des Polyèdres
- (en) Calendrier dodécaédrique rhombique (construire un calendrier dodécaédrique rhombique sans colle)
Solides géométriques Les polyèdres Les solides de Platon Tétraèdre - Cube - Octaèdre - Icosaèdre - Dodécaèdre Les solides d'Archimède Tétraèdre tronqué - Cube tronqué - Octaèdre tronqué - Dodécaèdre tronqué - Icosaèdre tronqué - Cuboctaèdre - Cube adouci - Icosidodécaèdre - Dodécaèdre adouci - Petit rhombicuboctaèdre - Grand rhombicuboctaèdre - Petit rhombicosidodécaèdre - Grand rhombicosidodécaèdre Les solides de Kepler-Poinsot Petit dodécaèdre étoilé - Grand dodécaèdre étoilé - Grand dodécaèdre - Grand icosaèdre Les solides de Catalan Triakioctaèdre - Tétrakihexaèdre - Triakitétraèdre - Pentakidodécaèdre - Triaki-icosaèdre - Dodécaèdre rhombique - Icositétraèdre pentagonal - Triacontaèdre rhombique - Hexacontaèdre pentagonal - Icositétraèdre trapézoïdal - Hexakioctaèdre - Hexacontaèdre trapézoïdal - Hexaki icosaèdre Les solides de Johnson Les solides de révolution Boule - Cylindre de révolution - Cône de révolution - Tore - Paraboloïde de révolution - Portail de la géométrie
Catégorie : Polyèdre
Wikimedia Foundation. 2010.