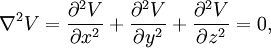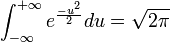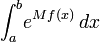- Pierre-simon laplace
-
Pierre-Simon Laplace
Pierre-Simon Laplace Naissance 23 mars 1749
Beaumont-en-AugeDécès 5 mars 1827 (à 77 ans)
ParisNationalité  France
FranceActivité(s) principale(s) Mathématicien, astronome, physicien Formation Université de Caen Distinctions Académie des sciences, Académie française Pierre-Simon Laplace, né le 23 mars 1749 à Beaumont-en-Auge et mort le 5 mars 1827 à Paris, est un mathématicien, astronome et physicien français.
Laplace est l’un des principaux scientifiques de la période napoléonienne ; en effet, il a apporté des contributions fondamentales dans différents champs des mathématiques, de l’astronomie et de la théorie des probabilités ; il a été l'un des scientifiques les plus influents de son temps, notamment par son affirmation du déterminisme ; il a contribué de façon décisive à l'émergence de l’astronomie mathématique reprenant et étendant le travail de ses prédécesseurs dans son traité intitulé Mécanique Céleste (1799-1825). Ce chef-d’œuvre, en cinq volumes, a transformé l’approche géométrique de la mécanique développée par Newton en une approche fondée sur l’analyse mathématique. En 1799 il est nommé ministre de l’intérieur sous le Consulat. Napoléon Ier, en 1806 lui confère le titre de comte de l’Empire. Il est nommé marquis en 1817, après la restauration des Bourbons[1].
Sommaire
Biographie
Enfance
Normand et fils d'un petit propriétaire terrien ou d’un ouvrier agricole, Simon Laplace doit son éducation à l’intérêt de quelques riches voisins pour ses capacités et pour sa belle prestance. On ne sait pas grand chose de ses premières années car il coupa les ponts, aussi bien avec ses parents qu’avec ses bienfaiteurs. Il semblerait que tout jeune, il devient l’assistant de l’école de Beaumont puis, après avoir terminé ses études à l’université de Caen, où il a comme professeur Christophe Gadbled, il rencontre d’Alembert, qui reconnaît son talent, l’encourage dans ses recherches et lui procure une lettre de recommandation grâce à laquelle il est nommé professeur de mathématiques à l’École militaire, poste peu exigeant qui lui laisse le temps de poursuivre ses études personnelles.
L’ascension
Confiant dans ses capacités, Laplace se voue à une recherche originale et durant dix-sept ans de 1771 à 1787, il produit une grande partie de sa contribution à l’astronomie. Son travail débute par un mémoire lu devant l’Académie française en 1773, dans lequel il montre que les mouvements planétaires sont restés voisins de ceux prévus par la théorie de Newton pour des longs intervalles de temps et il vérifie la relation jusqu’aux cubes de l’excentricité et de l’inclinaison des orbites. Plusieurs articles suivent sur certains points du calcul intégral, des différences finies, des équations différentielles et d’astronomie. Cependant certaines découvertes importantes proposées dans ces articles, comme les correspondances des harmoniques sphériques dans l’espace bidimensionnel ont déjà été publiées par Adrien-Marie Legendre dans un article envoyé à l’Académie en 1783.
En 1785, il devient pensionnaire de la chaire de mécanique de l’Académie royale des sciences, puis, en 1795, membre de la chaire de mathématiques du nouvel Institut des sciences et des arts, dont il est président en 1812. En 1816, il est élu à l’Académie française. En 1821, il devient lors de sa fondation le premier président de la Société de géographie. En outre, il devient membre de toutes les principales académies scientifiques d’Europe.
Par son intense activité académique, il exerce une grande influence sur les scientifiques de son temps, en particulier sur Lambert Adolphe Jacques Quételet et Siméon-Denis Poisson. Il est comparé à un Newton français pour son aptitude naturelle et extraordinaire pour les mathématiques. Il ne semble pas que Laplace ait été modeste et n'ait pas mesuré l'effet de son comportement. Anders Johan Lexell en visite à l’Académie des Sciences à Paris en 1780-1781 rapporte que Laplace laisse vraiment transparaître le fait qu’il se considère le meilleur mathématicien de son temps en France. [réf. nécessaire]
Laplace est l’un des premiers savants à s’intéresser de près à la question de la stabilité à long terme du système solaire. La complexité des interactions gravitationnelles entre le Soleil et les planètes connues à l’époque ne semblait pas admettre une solution analytique simple. Newton avait d’ailleurs déjà pressenti ce problème après avoir remarqué des irrégularités dans le mouvement de certaines planètes ; il en déduisait d’ailleurs qu’une intervention divine était nécessaire de manière à éviter la dislocation du système solaire.
Après ses travaux sur la mécanique céleste, Laplace se propose d’écrire un ouvrage qui aurait dû « offrir une solution complète au grand problème de la mécanique représenté par le système solaire et porter la théorie à coïncider aussi étroitement avec l’observation que les équations empiriques n’auraient plus trouver place dans les tables astronomiques. » Le résultat est contenu dans ses ouvrages Exposition du système du monde et Mécanique céleste.
Sa Mécanique céleste est publiée en cinq volumes. Les deux premiers, publiés en 1799, contiennent les méthodes pour calculer les mouvements des planètes, pour déterminer leurs formes et pour résoudre les problèmes liés aux marées. Le troisième et le quatrième, publiés respectivement en 1802 et en 1805, contiennent les applications de ces méthodes et diverses tables astronomiques. Le cinquième volume publié en 1825 est principalement historique mais il fournit en appendice les résultats des dernières recherches de Laplace. Celles-ci sont très nombreuses mais il s’approprie beaucoup de résultats d’autres scientifiques avec peu ou pas de reconnaissance et les conclusions sont souvent mentionnées comme si elles étaient les siennes. D’après Jean-Baptiste Biot, qui aide l’auteur dans la relecture avant impression, Laplace est fréquemment incapable de retrouver les détails des démonstrations et est ainsi souvent conduit à réétudier ses résultats pendant plusieurs jours.
Mécanique céleste n’est pas seulement la traduction des Principia Mathematica dans le calcul différentiel, mais complète certaines parties que Newton n’avait pas été en mesure de détailler.
Dans cet ouvrage, Laplace expose l’hypothèse de la nébuleuse selon lequel le système solaire se serait formé suite à la condensation d’une nébuleuse. L’idée de la nébuleuse avait déjà été énoncée par Kant en 1755, mais il est probable que Laplace n’en fut pas informé.
Laplace, qui avait effectué ses premiers travaux sur les probabilités entre 1771 et 1774, en redécouvrant notamment après Thomas Bayes les probabilités inverses, dites loi de Bayes-Laplace, ancêtre des statistiques inférentielles, publie en 1812 sa Théorie analytique des probabilités. Dans cet ouvrage, Laplace donne des éléments déterminants à la théorie des probabilités dont il est considéré comme un des pères. En 1814 il publie son Essai philosophique sur les probabilités. Il est le premier à publier la valeur de l’intégrale de Gauss. Il étudie la transformée de Laplace, étude plus tard complétée par Oliver Heaviside. Il adhère à la théorie d’Antoine Lavoisier, avec qui il détermine les températures spécifiques de plusieurs substances à l’aide d’un calorimètre de sa propre fabrication. En 1819, Laplace publie un simple résumé de son travail sur les probabilités.
Laplace est connu également pour son « démon de Laplace », lequel a la capacité de connaître, à un instant donné, tous les paramètres de toutes les particules de l’univers. Il formule ainsi le déterminisme généralisé, le mécanisme. L’état présent de l’univers est l’effet de son état antérieur, et la cause de ce qui va suivre. « Une intelligence qui, à un instant donné, connaîtrait toutes les forces dont la nature est animée, la position respective des êtres qui la composent, si d’ailleurs elle était assez vaste pour soumettre ces données à l’analyse, elle embrasserait dans la même formule les mouvements des plus grands corps de l’univers, et ceux du plus léger atome. Rien ne serait incertain pour elle, et l’avenir comme le passé seraient présents à ses yeux. » Dans cette perspective, l’auteur adopte une position déterministe, soit une position philosophique et scientifique capable d’inférer de ce qui est, ce qui sera. Ce concept de démon sera notamment remis en cause par le principe d'incertitude de Heisenberg.
Carrière politique
La capacité et la rapidité avec laquelle Laplace réussit à changer d’opinion politique est surprenante. Quand le pouvoir de Napoléon augmente, Laplace abandonne ses principes républicains (qui sont fidèlement le reflet des opinions du parti au pouvoir) et il implore le premier consul de lui donner le poste de ministre de l’Intérieur. Napoléon, qui désire le soutien des hommes de science, accepte la proposition mais, en moins de six semaines, la carrière politique de Laplace voit sa fin. Le bulletin de Napoléon à sa démission est le suivant : « Géomètre de première catégorie, Laplace n’a pas tardé à se montrer un administrateur plus que médiocre ; de son premier travail nous avons immédiatement compris que nous nous étions trompés. Laplace ne traitait aucune question d’un bon point de vue : il cherchait des subtilités de partout, il avait seulement des idées problématiques et enfin il portait l’esprit de l’infiniment petit jusque dans l’administration. »
Ainsi Laplace perd sa charge mais il maintient sa fidélité. Il entre au Sénat conservateur et, dans le troisième volume de la Mécanique céleste, il réalise une note dans laquelle il déclare qu’entre toutes les vérités contenues dans celui-ci, la plus chère à l’auteur est la déclaration faite à sa dévotion envers le médiateur de l’Europe. Dans le tirage vendu après la Restauration celle-ci est effacée. En 1814, il est évident que l’Empire allait faillir et Laplace se dépêche d’offrir ses services aux Bourbons. Durant la restauration, il est récompensé avec un titre de marquis. Le mépris que ses collègues ont à son égard en raison de sa conduite en cette occasion peut être lu dans les pages de Paul-Louis Courier. La connaissance de Laplace est utile pour les nombreuses commissions scientifiques auxquelles il appartient et probablement justifie la manière dont on ferma les yeux sur sa fausseté politique.
Que Laplace soit présomptueux et égoïste n’est nié par aucun de ses plus passionnés admirateurs ; sa conduite à l’égard de ses bienfaiteurs lors de sa jeunesse et envers ses amis politiques est ingrate et, de plus, il s’approprie les résultats de ceux qui sont relativement inconnus. Parmi ceux qu’il traite de cette manière, trois deviennent très connus : Adrien-Marie Legendre et Jean Baptiste Joseph Fourier en France et Thomas Young en Angleterre. Ceux-ci n’oublieront jamais l’injustice dont ils furent les victimes. D’autre part, sur certaines questions, il fait preuve d’un caractère indépendant et ne cache jamais sa manière de voir les questions de religion, de philosophie ou de science même si cela n’est pas apprécié des autorités au pouvoir. Vers la fin de sa vie, et spécialement pour les travaux de ses élèves, Laplace est généreux et une fois, il omet un de ses articles de sorte qu’un élève reçoive le mérite exclusif de la recherche. Initié franc-maçon, il est membre du collège des grands officiers du Grand Orient de France en 1804[2].
Contributions scientifiques
Mécanique céleste
Laplace apporte une importante contribution à la mécanique céleste en utilisant les conceptions lagrangiennes pour mieux expliquer le mouvement des corps. Il passe une grande partie de sa vie à travailler sur l’astronomie mathématique et son travail culmine avec la vérification de la stabilité dynamique du système solaire avec l’hypothèse que celui-ci consiste en un ensemble de corps rigides qui se meuvent dans le vide. Il établit seul l’hypothèse de la nébuleuse et il est un des premiers scientifiques à concevoir l’existence des trous noirs et la notion de collapsus gravitationnel.
Selon l’hypothèse de la nébuleuse, le système solaire se serait développé depuis une masse globulaire de gaz incandescent qui tourne autour d’un axe passant par son centre de masse. En refroidissant cette masse se serait réduite et quelques anneaux concentriques se seraient détachés de son bord externe. Ces anneaux en se refroidissant se seraient condensés en planètes. Le soleil représenterait le noyau central de la nébuleuse qui, resté encore incandescent, continue à irradier. De ce point de vue, nous devrions nous attendre que les planètes plus distantes soient plus vieilles que celles plus voisines du soleil. L’idée substantielle de la théorie, même avec quelques importantes modifications est acceptée encore aujourd’hui.
Laplace en outre conjecture le concept de trou noir. Il montre qu’il pourrait y avoir des étoiles massives dotées d’une gravité si grande que la lumière elle-même n'aurait pas une vitesse suffisante pour sortir de leur intérieur. Laplace suppose que certaines étoiles de la nébuleuse découvertes à l’aide des télescopes ne font pas partie de la Voie lactée et qu’elles sont elle-même des galaxies. Donc, Laplace anticipe la grande découverte de Edwin Hubble, un siècle avant que cela se produise.
Au cours des années 1784 à 1787, il produit plusieurs mémoires contenant des résultats exceptionnels. Parmi ceux-ci, celui de 1784 qui est particulièrement relevé, réimprimé dans le troisième volume de la Mécanique Céleste, à l’intérieur duquel il détermine complètement l’attraction d’un sphéroïde sur une particule externe à lui. Ceci est mémorable pour l’introduction en analyse des harmoniques sphériques ou coefficients de Laplace.
Si les coordonnées de deux points sont (r,μ,ω) et (r',μ',ω'), et si r' ≥ r, alors la réciproque de leur distance peut être développée en fonction du rapport de r/r', et les coefficients respectifs sont les coefficients de Laplace. Leur utilité dérive du fait que chaque fonction avec des coordonnées d’un point sur la sphère peut être développé en série de cette manière.
Cet article est aussi très important pour le développement de l’idée de potentiel, appropriée et utilisée par Joseph-Louis Lagrange dans ses mémoires de 1773, 1777 et 1780. Laplace montre que le potentiel satisfait toujours à l’équation différentielle:
et sur ce résultat, est basé son travail suivant sur l’attraction. La quantité
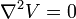 est définie comme la densité de
est définie comme la densité de 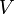 et sa valeur en chaque point indique l’excès de
et sa valeur en chaque point indique l’excès de 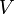 au regard à sa valeur moyenne autour du point. L’équation de Laplace ou la forme plus générale
au regard à sa valeur moyenne autour du point. L’équation de Laplace ou la forme plus générale 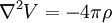 , apparaît dans toutes les branches de la physique mathématique.
, apparaît dans toutes les branches de la physique mathématique.Entre 1784 et 1786, il publie un mémoire concernant Jupiter et Saturne où il vérifie, par l’intermédiaire des séries perturbatives, que dans des temps très longs, l’action réciproque des deux planètes ne peut jamais influer significativement sur les excentricités et sur les inclinaisons de leurs orbites. Il fait noter que les particularités du système de Jupiter sont dues au fait que les mouvements moyens de Jupiter et Saturne sont très voisins de la commensurabilité. Il découvre aussi la cyclicité du mouvement des deux planètes estimée à peu près à 900 ans, les deux planètes paraissent exécuter des accélérations et des décélérations réciproques. De telles variations étaient déjà notées par Joseph-Louis Lagrange, mais seul Laplace les rattacha à un mouvement cyclique, confirmant l’idée que le système solaire présente des mouvements non occasionnels même à grande échelle temporelle. Les développements de ses études sur le mouvement planétaire sont exposés dans ses deux mémoires de 1788 et de 1789.
L’année 1787 est rendue mémorable par les analyses de Laplace sur les relations entre l’accélération lunaire et les changements séculaires dans l’excentricité de l’orbite de la Terre : Cette recherche complète la démonstration de la stabilité du système solaire entier. Il cherche par exemple à expliquer comment le mouvement orbital de la Lune subit une très légère accélération qui fait varier la longueur du mois lunaire d’une seconde en trois mille ans en attribuant la cause à une lente variation de l’excentricité terrestre. En vérité, il a été démontré successivement que de telles accélérations sont dues à l’attraction réciproque qui tend à synchroniser le mouvement de révolutions et de rotations des corps.
Physique
La théorie de l’attraction capillaire est due à Laplace, lequel accepte l’idée proposée par Francis Hauksbee dans Philosophical Transactions en 1709, selon laquelle le phénomène est dû à une force d’attraction qui est imperceptible à une distance raisonnable. La part qui s’occupe de l’action d’un solide sur un liquide et de l’action réciproque de deux liquides n’a pas été développée complètement, mais fut complétée en définitive par Carl Friedrich Gauss. En 1862 Lord Kelvin (Sir William Thomson) a démontré que, si nous supposons le caractère moléculaire de la matière, les lois de l’attraction peuvent être dotées des lois de Newton de la gravitation.
Laplace en 1816 est le premier à mettre en évidence explicitement le motif pour lequel la théorie de Newton du mouvement oscillatoire fournit une valeur imprécise de la vitesse du son. La vitesse effective est supérieure au regard de celle calculée par Newton à cause de la chaleur développé par la compression imprévue de l’air qui augmente l’élasticité et donc la vitesse du son transmis. Les recherches de Laplace en physique pratique se sont limitées à celles réalisées avec Antoine Lavoisier dans les années 1782 à 1784 sur la chaleur massique de différents corps.
Théorie des probabilités
Alors qu’il mène plusieurs recherches en physique, un autre thème auquel il dédie ses forces est la théorie des probabilités. Dans son Essai philosophique sur les probabilités, Laplace formalise la démarche mathématique de la logique par induction basée sur les probabilités, que nous reconnaissons aujourd’hui comme celle de Thomas Bayes. En 1774, il déduit le théorème de Bayes sans être probablement au courant du travail (publié en 1763) de Thomas Bayes (mort en 1761). Une formule très connue qui dérive de sa méthode est la règle de succession. Supposons qu’un évènement ait seulement deux tirages possibles valant « succès » et « insuccès ». Avec l’hypothèse que l’on sache peu ou rien a priori en rapport aux probabilités relatives aux tirages, Laplace détermine une formule de probabilité pour que le tirage suivant soit un succès :
où s est le nombre de succès observés précédemment et n est le nombre total des essais observés. Une telle formule est encore aujourd’hui utilisée comme une estimation de la probabilité d’un évènement si on connait l’espace des évènements, dont on dispose d’un petit nombre d’échantillons.
La règle de succession est sujette à beaucoup de critiques, dues en partie à l’exemple que Laplace choisit pour l’illustrer. En fait, il calcule la probabilité que le soleil se lèvera demain, considérant le fait qu’il s'était constamment levé depuis la plus ancienne époque de l’histoire, avec l’expression :
où d est le nombre de fois que le Soleil s'était levé dans le passé. Laplace estimait d à cinq mille ans ou à 1826313 jours. Ce résultat a été retenu comme absurde et certains auteurs ont conclu que toutes les applications des règles de successions sont absurdes par extension. Laplace était pleinement conscient de l’absurdité du résultat, immédiatement après l’exemple, il écrit Mais ce nombre [c’est-à-dire, la probabilité que le Soleil se lève demain] est beaucoup plus grand pour qui, considérant les principes qui règlent les jours et les saisons dans la totalité des évènements, réalise que nul dans l’instant actuel peut arrêter son cours.
Toujours en 1774 il explicita l’intégrale d'Euler :
mais il ne peut être considéré comme le père de la loi normale, parce qu’il ne l’associa pas aux lois sur les erreurs.
En 1779, Laplace indique la méthode pour estimer le rapport des cas favorables ramenés au nombre total de cas possibles. Ceci consiste à considérer les valeurs successives d’une quelconque fonction comme les coefficients du développement d’une autre fonction avec référencement à une variable différente. Cette seconde fonction est donc appelée la fonction génératrice de la précédente. Laplace démontre comment, par le moyen de l’interpolation, ces coefficients peuvent être déterminés à partir de la fonction génératrice. Ensuite, il traite le problème inverse, en trouvant à partir des coefficients la fonction génératrice au moyen de la résolution d’une équation aux différences finies. La méthode est peu pratique et, compte tenu des développements successifs des analyses, rarement utilisée aujourd’hui.
Son traité Théorie analytique des probabilités inclut un exposé de la méthode des moindres carrés, important témoignage de la paternité de Laplace sur les méthodes analytiques. La méthode des moindres carrés, par l’intermédiaire de nombreuses observations, est expliquée empiriquement par Carl Friedrich Gauss et Adrien-Marie Legendre, mais le quatrième chapitre de ce travail contient une démonstration formelle de celui-ci, sur laquelle depuis s’est basée toute la théorie des erreurs.
Mathématiques
Parmi les découvertes mineures de Laplace en mathématiques pures, on peut mentionner sa discussion (avant Alexandre-Théophile Vandermonde) de la théorie générale des déterminants en 1772 : sa démonstration que n’importe quelle équation paire doit avoir au moins un facteur quadratique réel, sa réduction de la solution des équations différentielles linéaires à intégrales définies ; et sa solution à l’équation différentielle linéaire partielle du second ordre. Il est l'inventeur de la méthode de variation des constantes, permettant de résoudre les équations différentielles linéaires avec second membre, lorsque l'on connaît la solution de l'équation sans second membre. Il est aussi le premier à considérer les difficiles problèmes dans les équations aux différences mixtes, et à démontrer que la solution d’une équation aux différences finies de premier grade et du second ordre pourrait être toujours obtenue sous la forme d’une fraction continue. En plus de ces découvertes originales, il détermine, dans sa théorie des probabilités, les valeurs des plus communes intégrales définies; et dans le même livre, il donne la démonstration générale du théorème énoncé par Joseph-Louis Lagrange pour le développement en série d’une fonction quelconque impliquée au moyen de coefficients différentiels.
La transformée de Laplace, par contre, bien qu’elle soit appelée ainsi en son honneur parce qu’il l’utilisa dans son travail sur la théorie des probabilités, fut découverte à l’origine par Leonhard Euler. La transformée de Laplace apparaît dans toutes les branches de la physique mathématique - champ d’étude auquel Laplace contribua de manière importante.
En mathématiques appliquées on lui doit également la Méthode de Laplace qui permet d'estimer des intégrales de la forme:
quand M est grand.
Convictions philosophiques
À la différence de beaucoup d’autres mathématiciens, Laplace ne donne pas aux mathématiques un statut particulier, il y voit plutôt un instrument utile pour la recherche scientifique et pour les problèmes pratiques. Par exemple, Laplace a considéré l’analyse comme un outil pour affronter les problèmes physiques, tout en se montrant extrêmement habile pour inventer les concepts dont il a besoin pour atteindre cet objectif. Tant que ses résultats ne sont pas avérés, il ne se préoccupe pas d’expliquer les phases démonstratives ; il ne soigne pas l’élégance ; pour lui, n'importe quel moyen est bon s'il permet de résoudre le problème qui le préoccupe.
Il croit fermement au déterminisme causal comme il l'écrit dans l'introduction de son ouvrage sur les probabilités:
« Nous pouvons considérer l’état actuel de l’univers comme l’effet de son passé et la cause de son futur. Une intelligence qui à un instant déterminé devrait connaitre toutes les forces qui mettent en mouvement la nature, et toutes les positions de tous les objets dont la nature est composée, si cette intelligence fut en outre suffisamment ample pour soumettre ces données à analyse, celle-ci renfermerait dans une unique formule les mouvements des corps plus grands de l’univers et des atomes les plus petits ; pour une telle intelligence nul serait incertain et le propre futur comme le passé serait évident à ses yeux »— Essai philosophique sur les probabilités, Pierre-Simon Laplace
Il est souvent fait référence à cette intelligence comme au « démon de Laplace » (de manière analogue au démon de Maxwell). La description de l’hypothétique intelligence décrite au sujet de Laplace comme un petit diable ne vient pas pourtant de Laplace, mais de biographies excessives : Laplace espérait que l’humanité aurait amélioré sa compréhension scientifique du monde et croyait que, si elle fut complétée, elle aurait encore eu besoin d’une extraordinaire capacité de calcul pour la déterminer complètement en tout instant particulier. Cette question de la possibilité d'atteindre par le calcul des prévisions fiables dans les domaines complexes ne sera mise en doute qu'avec les travaux de Henri Poincaré, et ne touchera le grand public qu'avec la théorie du chaos. Entretemps, l'opposition à ce sujet entre Von Neumann et Wiener est restée célèbre.
Il a été récemment[Quand ?] proposé une limite sur l’efficacité du calcul de l’univers, c’est-à-dire sur l’habileté du petit diable de Laplace à traiter une quantité infinie d’informations. La limite fait référence à l'entropie maximale de l’univers, à la vitesse de la lumière et à la quantité minimum de temps nécessaire pour transporter l’information sur une longueur égale à la longueur de Planck ; celle-ci étant égale à 2130 bit. En conséquence, n’importe quelle chose demandant plus que cette quantité de données ne peut être calculée dans la quantité de temps qui est passée jusqu’à présent dans l’univers.
Même si Laplace pense à une intelligence supérieure, il ne pense seulement qu’à une expérience de pensée, une supposition. Il ne croit pas véritablement en l’existence d’une telle intelligence, il est le symbôle de athéisme scientifique [3] ou plus ou moins agnostique comme le montre l’anecdote suivante :
Laplace vint un jour faire hommage à Napoléon d’un exemplaire de son ouvrage, et le récit suivant de l’entrevue peint d’une façon caractéristique les caractères des deux hommes. On avait dit à Napoléon que l’ouvrage ne faisait nulle part mention du nom de Dieu et, comme Napoléon aimait à poser des questions embarrassantes, il fit, en acceptant l’ouvrage, cette remarque : « M. Laplace, on me dit que vous avez écrit ce volumineux ouvrage sur le système de l’Univers sans faire une seule fois mention de son Créateur ». Laplace, bien que souple courtisan, avait sur tous les points qui touchaient à sa philosophie, l’obstination du martyr ; il se redressa aussitôt et répondit brusquement : « Sire, je n’ai pas eu besoin de cette hypothèse. » Napoléon, grandement amusé, fit part de cette réponse à Lagrange, qui s’écria : « Ah ! c’est une belle hypothèse ; elle explique beaucoup de choses.[4] » Napoléon répéta cette réponse à Laplace, qui répondit habilement que si cette hypothèse explique tout, elle ne permet de prédire rien et n'entrait donc pas dans son domaine d'étude (cité par Richard Dawkins).
Hommages
- L'astéroïde (4628) Laplace a été nommé en son honneur[5].
- Son nom est inscrit sur la Tour Eiffel.
- Grand Officier de la Légion d'Honneur.
- Marquis et Pair de France
Notes et références
- ↑ Biographie de l’Académie française
- ↑ Dictionnaire de la Franc-Maçonnerie, PUF, 1987
- ↑ Science de la nature et théologie
- ↑ Walter William Rouse Ball, Histoire des mathématiques, Paris, Librairie Scientifique A . Hermann, 1906 p.104-105.
- ↑ (en) L. D. Schmadel, Dictionary of Minor Planet Names, 5th rev. ed., Springer-Verlag, Berlin, 2003 (ISBN 3-540-00238-3)
Voir aussi
Ouvrages
- Textes de vulgarisation
- Exposition du système du monde, Bachelier, Paris, 1836. Texte en ligne Réédité dans la collection Corpus des œuvres de philosophie en langue française, Fayard, Paris, 1984. (ISBN 2213014779)
- Textes techniques
- Œuvres complètes de Laplace, publiées sous les auspices de l’Académie des sciences par MM. les secrétaires perpétuels, Gauthier-Villars, Paris, 14 volumes, 1878-1912. Comprend : I-V. Traité de mécanique céleste ; VI. Exposition du système du monde ; VII. 1-2. Théorie analytique des probabilités ; VIII-XII. Mémoires extraits des recueils de l’Académie des sciences de Paris et de la classe des sciences mathématiques et physiques de l’Institut de France ; XIII-XIV. Mémoires divers. Tables. Texte en ligne.
- Théorie analytique des probabilités, Tome VII des œuvres complètes, Paris, 3e édition, 1820. Texte en ligne Réédition : Jacques Gabay, 1995. (ISBN 2-87647-161-2).
Bibliographie
- (en) E.T. Bell Men of Mathematics: The Lives and Achievements of the Great Mathematicians from Zeno to Poincaré New York, Simon and Schuster, 1986, Ch. 11
- (it) Carl Boyer, Storia della matematica, Milano: Mondadori, 2004. (ISBN 88-04-33431-2)
- (en) Charles Coulston Gillispie, avec la collaboration de Robert Fox et Ivor Grattan-Guinnsess, Pierre-Simon Laplace, 1749-1827: A Life in Exact Science, Princeton University Press, 1997. (ISBN 0-691-05027-9)
- (fr) Roger Hahn, Le Système du monde - Pierre Simon Laplace, un itinéraire dans la science, Collection « Bibliothèque des histoires », Gallimard, Paris, 2004. (ISBN 2-07-072936-2)
- (it) Mirella Fortino (a cura di) Il caso. Da Pierre-Simon Laplace a Emile Borel (1814-1914)
- (fr) Alphonse Rebière, Mathématiques et mathématiciens, 3e Paris, Nony & Cie, 1898
- (it) Paolo Rossi (diretta da) Storia della scienza vol. 2
- De Laplace
- (it)Saggio filosofico sulle probabilità Theoria - Editori Associati, 1987 (ISBN 88-241-0040-6)
- (it)Storia dell’astronomia Cuen, 1997 (ISBN 88-7146-368-4)
Œuvres en ligne
- Ses œuvres en ligne sur Gallica
Articles connexes
- Certitude
- Mécanique céleste
- Opérateur laplacien
- Potentiel gravitationnel
- Probabilité
- Problème à N corps
Liens et documents externes
- Biographie de l’Académie française
- (en) Biographie in MacTutor
- [pdf] Pierre Simon de Laplace, savant normand, cahier des archives départementales du Calvados n°15 en téléchargement gratuit.
Sources
- (it) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en italien intitulé « Pierre Simon Laplace ».
 du 18.08.2007
du 18.08.2007
Précédé par Pierre-Simon Laplace Suivi par Nicolas-Marie Quinette Ministre français de l'Intérieur (1799) Lucien Bonaparte Précédé par
Michel Regnaud de Saint-Jean d'AngélyFauteuil 8 de l’Académie française
1816-1827Suivi par
Pierre-Paul Royer-Collardcasse toi sale puteeeee
- Portail de la géodésie et de la géophysique
- Portail de l’astronomie
- Portail des mathématiques
- Portail de la physique
- Portail du Premier Empire
Catégories : Physicien | Physicien français | Mathématicien | Mathématicien français | Astronome | Astronome français | Probabiliste | Personnalité normande | Membre de l'Académie des sciences (France) | Membre de l'Académie française | Académie de Caen | Grand officier de la Légion d'honneur | Membre de la Société philomathique de Paris | Membre du Sénat conservateur | Comte de l'Empire | Ancien étudiant de l'université de Caen | Savants de la Tour Eiffel | Naissance en 1749 | Naissance en Normandie | Décès en 1827
Wikimedia Foundation. 2010.