Equation de Laplace

Equation de Laplace: Équation de Laplace

Articles d'analyse vectorielle

Objets d'étude

Champ vectoriel Champ scalaire

Équation aux dérivées partielles

de Laplace de Poisson

Opérateurs

Nabla Gradient

Rotationnel Divergence

Laplacien scalaire Bilaplacien

Laplacien vectoriel D'alembertien

Théorèmes

de Green de Stokes

de Helmholtz de flux-divergence

du gradient du rotationnel

En analyse vectorielle, l'équation de Laplace est une équation aux dérivées partielles du second ordre, dont le nom est un hommage au physicien mathématicien Pierre-Simon Laplace.

Introduite pour les besoins de la mécanique newtonienne, l'équation de Laplace apparait dans de nombreuses autres branches de la physique théorique : astronomie, électrostatique, mécanique des fluides, propagation de la chaleur, diffusion, mouvement brownien, mécanique quantique.

Toute fonction solution de l'équation de Laplace est dite harmonique.

Sommaire

1 Équation de Laplace à trois dimensions

2 Équation de Laplace à deux dimensions

2.1 Rappels sur les fonctions holomorphes

2.2 Résultats sur l'équation de Laplace et les fonctions holomorphes

2.2.1 Premier théorème

2.2.2 Démonstration

2.2.3 Second théorème

2.2.4 Démonstration

3 Équation de Poisson

4 Articles liés

5 Notes

Équation de Laplace à trois dimensions

En coordonnées cartésiennes dans un espace euclidien de dimension 3, le problème consiste à trouver toutes les fonctions à trois variables réelles $ψ(x, y, z)$ qui vérifient l'équation aux dérivées partielles^[1] du second ordre :
$\frac{\partial^2 \psi}{\partial x^2} \ + \ \frac{\partial^2 \psi}{\partial y^2} \ + \ \frac{\partial^2 \psi}{\partial z^2} \ = \ 0$
Pour simplifier l'écriture, on introduit un opérateur différentiel noté $Δ$ et appelé opérateur de Laplace, ou simplement laplacien, tel que l'équation aux dérivées partielles précédente s'écrive de façon compacte :
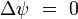
$\Delta \psi \ = \ 0$
Équation de Laplace à deux dimensions

En coordonnées cartésiennes dans un espace euclidien de dimension 2, le problème consiste à trouver toutes les fonctions à deux variables réelles $V (x, y)$ qui vérifient :
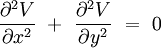
$\frac{\partial^2 V}{\partial x^2} \ + \ \frac{\partial^2 V}{\partial y^2} \ = \ 0$
On montre que toute fonction holomorphe donne des solutions de l'équation de Laplace à deux dimensions par leur partie réelle et par leur partie imaginaire ; de plus, ces solutions sont orthogonales en tout point.

Rappels sur les fonctions holomorphes

Toute fonction polynomiale à coefficients complexes est holomorphe sur $\mathbb C$ ; aussi le sont les fonctions trigonométriques et la fonction exponentielle. (Les fonctions trigonométriques sont en fait relativement proches de la fonction exponentielle puisqu'elles peuvent être définies à partir de celle-ci en utilisant les formules d'Euler).

La fonction logarithme est holomorphe sur l'ensemble des nombres complexes privé de la demi-droite des réels négatifs (on parle de "coupure").

La fonction racine carrée peut être définie par 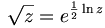$\sqrt{z} = e^{{1 \over 2} \ln{z}}$ et est ainsi holomorphe partout où la fonction logarithme l'est.

Les fonctions trigonométriques réciproques ont de la même manière des coupures et sont holomorphes partout sauf aux coupures.

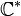La fonction inverse $z\mapsto 1/z$ est holomorphe sur $\mathbb C^*$ .

Résultats sur l'équation de Laplace et les fonctions holomorphes

Premier théorème

Théorème — Toute fonction analytique est solution de l'équation de Laplace.

Démonstration

On introduit la variable complexe : $z = x + i y$ où $i 2 = - 1$ , et on définit la fonction holomorphe $F (z)$ . Par dérivation , on obtient que :
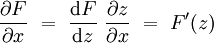
$\frac{\partial F}{\partial x} \ = \ \frac{\mathrm d F}{\mathrm dz} \ \frac{\partial z}{\partial x} \ = \ F'(z)$
alors que :
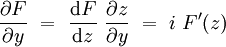$\frac{\partial F}{\partial y} \ = \ \frac{\mathrm dF}{\mathrm dz} \ \frac{\partial z}{\partial y} \ = \ i \ F'(z)$ .
En dérivant une seconde fois, on obtient d'une façon similaire :
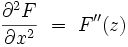
$\frac{\partial^2 F}{\partial x^2} \ = \ F''(z)$
alors que :
$\frac{\partial^2 F}{\partial y^2} \ = \ - \ F''(z)$
La somme est nulle, donc la fonction holomorphe F est bien une solution de l'équation de Laplace :
$\frac{\partial^2 F}{\partial x^2} \ + \ \frac{\partial^2 F}{\partial y^2} \ = \ 0$
Remarque : la fonction holomorphe admet toujours une décomposition en partie réelle et partie imaginaire :
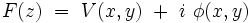
$F(z) \ = \ V(x,y) \ + \ i \ \phi(x,y)$
En annulant la partie réelle et la partie imaginaire séparément, on obtient deux équations de Laplace indépendantes :
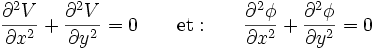
$\frac{\partial^2 V}{\partial x^2}+ \frac{\partial^2 V}{\partial y^2}=0 \qquad \mathrm{et :} \qquad \frac{\partial^2 \phi}{\partial x^2}+ \frac{\partial^2 \phi}{\partial y^2}=0$
Second théorème

Théorème — Les équipotentielles sont perpendiculaires aux lignes de champ.

Démonstration

On peut écrire :
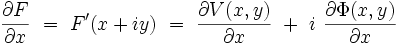
$\frac{\partial F}{\partial x}\ = \ F'(x+iy) \ = \ \frac{\partial V(x,y)}{\partial x} \ + \ i \ \frac{\partial \Phi(x,y)}{\partial x}$
et :
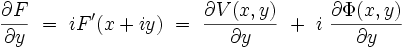
$\frac{\partial F}{\partial y} \ = \ i F'(x+iy) \ = \ \frac{\partial V(x,y)}{\partial y} \ + \ i \ \frac{\partial \Phi(x,y)}{\partial y}$
On en déduit :
$\frac{\partial V(x,y)}{\partial x} \ = \ \frac{\partial \Phi(x,y)}{\partial y} \qquad \mathrm{et :} \qquad \frac{\partial \Phi(x,y)}{\partial x} \ = \ - \ \frac{\partial V(x,y)}{\partial y}$
soit finalement :
$\frac{\partial V(x,y)}{\partial x} \cdot \frac{\partial \Phi(x,y)}{\partial x} \ + \ \frac{\partial V(x,y)}{\partial y} \cdot \frac{\partial \Phi(x,y)}{\partial y} \ = \ 0$
On reconnait là le produit scalaire des deux vecteurs :
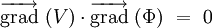
$\overrightarrow\operatorname{grad} \ (V) \cdot\overrightarrow\operatorname{grad} \ (\Phi) \ = \ 0$
On en déduit que les courbes à « $V(x,y)$ = constante » et « $φ(x,y)$ = constante » sont perpendiculaires (transformation conforme). Ce qui fait que si « $V(x,y)$ = constante » représente les courbes de même potentiel, alors « $φ(x,y)$ = constante » représente les lignes de champ électrique en électrostatique

Équation de Poisson

Si le membre de droite est une fonction donnée $f (x, y, z)$ , on obtient l'équation de Poisson :
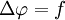
$\Delta \varphi = f$
Articles liés

Opérateur laplacien

Théorie du potentiel

Équation de Poisson

Analyse complexe

Notes

↑ Comme pour toute équation aux dérivées partielles, il faut en général spécifier des conditions aux limites pour que le problème soit mathématiquement « bien posé ». Il se peut cependant que le problème soit mal posé, bien que des conditions aient été fixées (par exemple, des conditions aux limites de Neumann sur l'entièreté du bord du domaine). Aucune condition initiale n'est nécessaire, en revanche.

Portail des mathématiques

Portail de la physique

Ce document provient de « %C3%89quation de Laplace ».

Catégories : Analyse fonctionnelle | Analyse à plusieurs variables | Équation aux dérivées partielles | Mécanique | Physique théorique

Contenu soumis à la licence CC-BY-SA. Source : Article Equation de Laplace de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Équation de laplace — Articles d analyse vectorielle Objet … Wikipédia en Français
Équation de Laplace — En analyse vectorielle, l équation de Laplace est une équation aux dérivées partielles du second ordre, dont le nom est un hommage au physicien mathématicien Pierre Simon de Laplace. Introduite pour les besoins de la mécanique newtonienne, l… … Wikipédia en Français
Equation de Poisson — Équation de Poisson Pour les articles homonymes, voir Poisson (homonymie). Articles d analyse vectorielle … Wikipédia en Français
Équation de poisson — Pour les articles homonymes, voir Poisson (homonymie). Articles d analyse vectorielle … Wikipédia en Français
Equation aux derivees partielles — Équation aux dérivées partielles En mathématiques, plus précisément en calcul différentiel, une équation aux dérivées partielles ou équation différentielle partielle (EDP) est une équation dont les solutions sont les fonctions inconnues vérifiant … Wikipédia en Français
Équation différentielle partielle — Équation aux dérivées partielles En mathématiques, plus précisément en calcul différentiel, une équation aux dérivées partielles ou équation différentielle partielle (EDP) est une équation dont les solutions sont les fonctions inconnues vérifiant … Wikipédia en Français
Équation de Poisson — Pour les articles homonymes, voir Poisson (homonymie). En analyse vectorielle, l équation de Poisson (ainsi nommée en l honneur du mathématicien et physicien français Siméon Denis Poisson) est l équation aux dérivées partielles du second ordre… … Wikipédia en Français
Équation aux dérivées partielles — En mathématiques, plus précisément en calcul différentiel, une équation aux dérivées partielles (EDP) est une équation dont les solutions sont les fonctions inconnues vérifiant certaines conditions concernant leurs dérivées partielles. Une EDP a… … Wikipédia en Français
Laplace — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sommaire 1 Patronyme 2 Toponyme 3 Science … Wikipédia en Français
Equation differentielle — Équation différentielle En mathématiques, une équation différentielle est une relation entre une ou plusieurs fonctions inconnues et leurs dérivées. L ordre d une équation différentielle correspond au degré maximal de différenciation auquel une… … Wikipédia en Français

Mark and share
Search through all dictionaries
Translate…
Search Internet

Share the article and excerpts