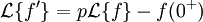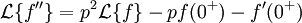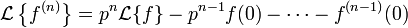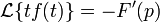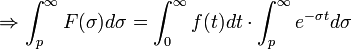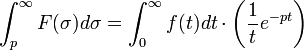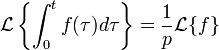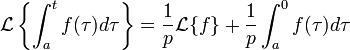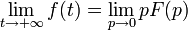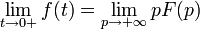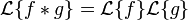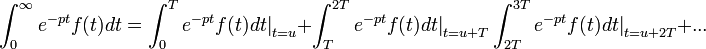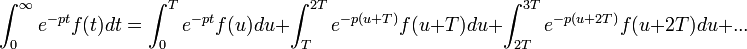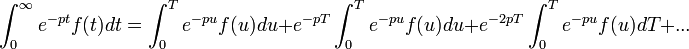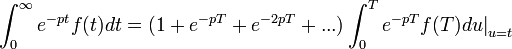- Transformee de Laplace
-
Transformée de Laplace
 Pour les articles homonymes, voir Laplace.
Pour les articles homonymes, voir Laplace.Sommaire
Définition
En mathématiques et en particulier en analyse fonctionnelle, la transformée de Laplace monolatérale d'une fonction f d'une variable réelle positive t est la fonction F de la variable complexe p, définie par:
Les propriétés de cette transformation lui confèrent une grande utilité dans l'analyse des systèmes dynamiques linéaires. La plus intéressante de ces propriétés est que l'intégration et la dérivation sont transformées en division et multiplication par p, de la même manière que le logarithme transforme la multiplication en addition. Elle permet ainsi de ramener la résolution des équations différentielles linéaires à coefficients constants à la résolution d'équations affines (dont les solutions sont des fonctions rationnelles de p) (voir Application de la transformation de Laplace aux équations différentielles).
La transformation de Laplace est très utilisée par les ingénieurs pour résoudre des équations différentielles et déterminer la fonction de transfert d'un système linéaire. Par exemple, en électronique, contrairement à la décomposition de Fourier qui est utilisée pour la détermination du spectre d'un signal périodique ou même quelconque, elle tient compte de l'existence d'un régime transitoire précédant le régime permanent (exemple : la prise en compte de l'allure du signal avant et après la mise en marche d'un générateur de fréquence).Il suffit en effet de transposer l'équation différentielle dans le domaine de Laplace pour obtenir une équation beaucoup plus simple à manipuler.
Par exemple, lors de l'étude d'une machine à courant continu :
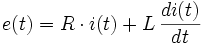 dans le domaine temporel devient
dans le domaine temporel devient 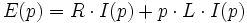 dans le domaine de Laplace. Attention, ceci n'est valable dans ce cas que si les conditions initiales du signal i(t) sont nulles.
dans le domaine de Laplace. Attention, ceci n'est valable dans ce cas que si les conditions initiales du signal i(t) sont nulles.
On a utilisé ici des propriétés de la transformation de Laplace, explicitées ci-dessous.Remarque : la notation "s" (variable de Laplace) est souvent utilisée dans les pays anglo-saxons alors que la notation "p" est utilisée notamment en France et en Allemagne. La transformation de Laplace est obligatoirement appliquée à des signaux causaux c’est-à-dire nuls avant t=0. (Pour les signaux non causaux des astuces de décalages existent)
On définit aussi la transformation de Laplace-Carson par[1] :
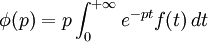 qui permet d'associer à toute fonction d'une variable
qui permet d'associer à toute fonction d'une variable 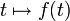 une fonction image
une fonction image 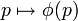
Cette transformée est utilisée de préférence par les ingénieurs car :
- Une constante a pour image la même constante,
- Les équations aux dimensions (et donc l'homogénéité) des expressions sont conservées par la transformation,
- Plus grande facilité d'emploi en calcul matriciel et tensoriel.
Inversion
L'inversion de la transformation de Laplace s'effectue par le moyen d'une intégrale dans le plan complexe. On démontre presque sans difficulté que pour t positif,
où γ est choisi pour que l'intégrale soit convergente, ce qui implique que γ soit supérieur à la partie réelle de toute singularité de F(p).
Pratiquement, dans les cas généraux, on rapproche les formules dans l'univers de Laplace aux formules connues pour utiliser la table de transformée inverse.
Propriétés
Linéarité
Dérivation
Soit à calculer :
En intégrant par parties, on obtient :
soit finalement (et de proche en proche ou par récurrence pour les dérivations successives) :
- La cinquième formule peut se démontrer de cette manière:
- On part de la définition de
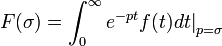
- puis :

- Soit, en évaluant l'intégrale
- qui est aussi la transformée de
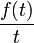 c'est-à-dire
c'est-à-dire 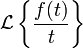
- C’est-à-dire :
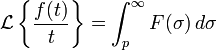
Intégration
Valeur finale
Valeur initiale
Convolution
Il faut faire attention aux ensembles sur lesquels sont définies les fonctions f et g. En effet, la convolution et la transformée de Laplace imposent des conditions pas toujours compatibles. Le plus simple est de les définir sur
 en les multipliant par la fonction indicatrice de leur ensemble de définition initial.
en les multipliant par la fonction indicatrice de leur ensemble de définition initial.Transformée de Laplace d'une fonction de période T
- On peut montrer la formule de la manière suivante :
On regroupe les termes :
Alors,
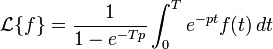
Quelques transformées usuelles
La transformée de Laplace n'est valide que pour des t supérieurs à
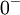 c'est pour cela que toutes les fonctions qui suivent dans cette table sont multiples ou composées de u(t) (fonction échelon unité).
c'est pour cela que toutes les fonctions qui suivent dans cette table sont multiples ou composées de u(t) (fonction échelon unité).Fonction Domaine temporel
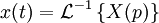
Transformée de Laplace
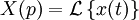
Région de convergence 1 délai idéal 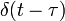
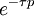
1a impulsion unité 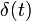
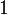
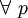
2 retard à la n-ième puissance avec décalage fréquenciel 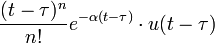
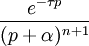
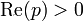
2a puissance n-ième 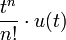
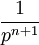
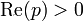
2a.1 puissance q-ième 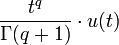
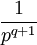
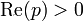
2a.2 échelon unité (Heaviside) 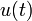
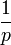
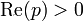
2b échelon retardé 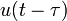
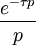
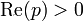
2c rampe 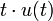
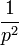
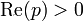
2d retard avec décalage fréquentiel 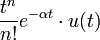
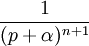
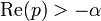
2d.1 décroissance exponentielle 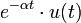
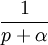
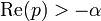
3 approche exponentielle 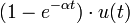
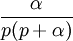
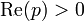
4 sinus 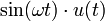
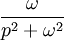
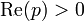
5 cosinus 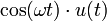
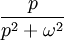
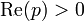
6 sinus hyperbolique 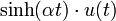
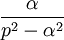
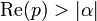
7 cosinus hyperbolique 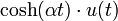
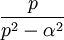
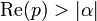
8 Décroissance exponentielle
d'une onde sinusoidale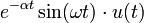
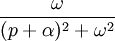
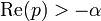
9 Décroissance exponentielle
d'une onde cosinusoidale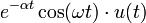
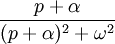
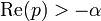
10 n-ième racine ![\sqrt[n]{t} \cdot u(t)](/pictures/frwiki/52/486b3056c275d0abfe2730f87a747f9f.png)
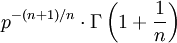
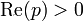
11 logarithme 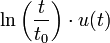
![- { t_0 \over p} \ [ \ \ln(t_0 p)+\gamma \ ]](/pictures/frwiki/52/43a060cf20d3f805a0f732231c7cb902.png)
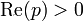
12 Fonction de Bessel
du premier type,
d'ordre n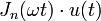
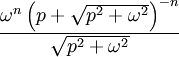
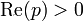
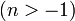
13 Fonction de Bessel modifiée
du premier type,
d'ordre n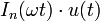
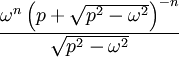
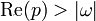
14 Fonction d'erreur 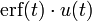
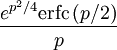
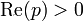
Notes: 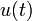 représente la fonction de Heaviside.
représente la fonction de Heaviside.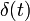 représente la fonction de Dirac.
représente la fonction de Dirac.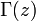 est la fonction Gamma.
est la fonction Gamma.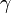 est la constante d'Euler-Mascheroni.
est la constante d'Euler-Mascheroni.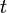 , est un nombre réel, il représente typiquement le temps,
, est un nombre réel, il représente typiquement le temps,
mais peut désigner n'importe quelle autre quantité.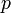 est un nombre complexe.
est un nombre complexe.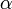 ,
, 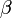 ,
, 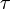 , et
, et 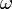 sont des nombres réels.
sont des nombres réels. est un entier.
est un entier.
Notes & références
- ↑ M. Denis-Papin et A. Kaufmann, Cours de calcul opérationnel appliqué, Éditions Albin Michel, Paris, 1967
Voir aussi
Lien interne
Lien externe
- Portail des mathématiques
Catégories : Transformée | Analyse fonctionnelle
Wikimedia Foundation. 2010.

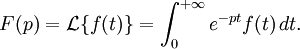

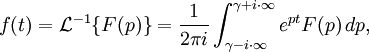
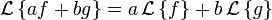
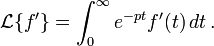
![\mathcal{L}\{f'\}
= \left[e^{-pt}f(t)\right]_0^\infty + p\int_0^{\infty} e^{-pt} f(t)\,dt\,,](/pictures/frwiki/98/b5238685563e073f1f890a5a8d051ece.png)