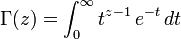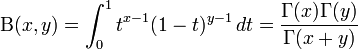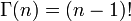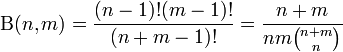Integrale d'Euler

Integrale d'Euler

Intégrale d'Euler

En mathématiques, on désigne par intégrales d'Euler ou intégrales eulériennes deux types d'intégrales :

  1. L'intégrale d'Euler de première espèce aussi appelée fonction gamma :
    \Gamma(z) = \int_0^\infty t^{z-1}\,e^{-t}\,dt
  2. L'intégrale d'Euler de seconde espèce aussi appelée fonction bêta :
    \mathrm{\Beta}(x,y)= \int_0^1t^{x-1}(1-t)^{y-1}\,dt =\frac{\Gamma(x)\Gamma(y)}{\Gamma(x+y)}

Pour m et n entiers strictement positifs :

\Gamma(n) = (n-1)! \,
\mathrm{\Beta}(n,m)= {(n-1)!(m-1)! \over (n+m-1)!}={n+m \over nm{n+m \choose n}}


Voir aussi

Articles connexes

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Int%C3%A9grale d%27Euler ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Integrale d'Euler de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Intégrale d'Euler — En mathématiques, on désigne par intégrales d Euler ou intégrales eulériennes deux types d intégrales : L intégrale d Euler de première espèce aussi appelée fonction bêta : L intégrale d Euler de seconde espèce aussi appelée fonction… …   Wikipédia en Français

  • Intégrale à paramètre — Intégrale paramétrique En mathématiques, une intégrale paramétrique (également appelée intégrale à paramètre) est une fonction définie à partir de l intégration d une fonction de plusieurs variables sur un ensemble fixe par rapport à une partie… …   Wikipédia en Français

  • Intégrale à paramètres — Intégrale paramétrique En mathématiques, une intégrale paramétrique (également appelée intégrale à paramètre) est une fonction définie à partir de l intégration d une fonction de plusieurs variables sur un ensemble fixe par rapport à une partie… …   Wikipédia en Français

  • Integrale indefinie — Intégrale indéfinie En analyse réelle ou complexe, une intégrale indéfinie d une fonction f intégrable sur un intervalle I est une fonction définie sur I par où a est un élément de I et K une constante[1] Lorsque f est une fonction continue, F… …   Wikipédia en Français

  • Intégrale Indéfinie — En analyse réelle ou complexe, une intégrale indéfinie d une fonction f intégrable sur un intervalle I est une fonction définie sur I par où a est un élément de I et K une constante[1] Lorsque f est une fonction continue, F est une primitive de f …   Wikipédia en Français

  • Integrale de Gauss — Intégrale de Gauss Pour tout réel strictement positif α, la fonction (paire) est intégrable sur et : . Cette intégrale est appelée intégrale de Gauss. Elle intervient dans la définition de la loi de probabilité appelée loi gaussienne, ou loi …   Wikipédia en Français

  • Intégrale De Gauss — Pour tout réel strictement positif α, la fonction (paire) est intégrable sur et : . Cette intégrale est appelée intégrale de Gauss. Elle intervient dans la définition de la loi de probabilité appelée loi gaussienne, ou loi normale. La valeur …   Wikipédia en Français

  • Intégrale de gauss — Pour tout réel strictement positif α, la fonction (paire) est intégrable sur et : . Cette intégrale est appelée intégrale de Gauss. Elle intervient dans la définition de la loi de probabilité appelée loi gaussienne, ou loi normale. La valeur …   Wikipédia en Français

  • Intégrale paramétrique — En mathématiques, et plus précisément en analyse, une intégrale paramétrique (également appelée intégrale à paramètre) est une fonction d une variable, définie à partir d une fonction de deux variables – la variable d intégration et le paramètre… …   Wikipédia en Français

  • Intégrale définie — Table d intégrales Intégrales définies On appelle intégrale définie dans l intervalle [a,b] lorsque est une primitive quelconque de et que et …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”