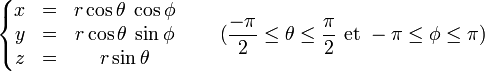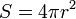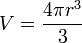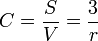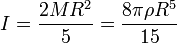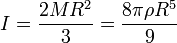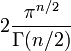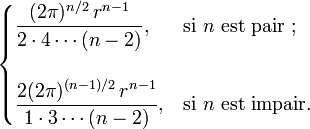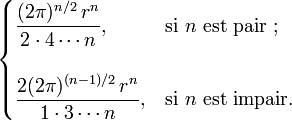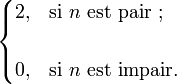Sphères

Sphères

Sphère

Page d'aide sur l'homonymie Pour les articles homonymes, voir Sphère (homonymie).
Une sphère dans un espace euclidien

En géométrie euclidienne, une sphère est une surface plongée dans l'espace à trois dimensions, dont tous les points sont situés à une même distance d'un point appelé centre. La valeur de cette distance au centre est appelée le rayon de la sphère. Elle n'inclut donc pas les points situés à une distance inférieure au rayon, au contraire de la boule.

La surface de la Terre ne constitue pas une sphère parfaite mais sa forme en est proche (on parle de sphéroïde[1]), d'où le terme « géosphère » pour désigner les couches enveloppant la terre (lithosphère, hydrosphère, atmosphère et biosphère notamment[2]).

Plus généralement, dans un espace vectoriel normé voire dans un espace métrique, une sphère est l'ensemble des points à même distance d'un centre. Leur forme peut alors être très différente de la forme ronde usuelle. Les sphères des espaces euclidiens constituent des objets fondamentaux en topologie algébrique.

La déformation d'une sphère par une transformation affine produit un ellipsoïde. Le ballon de rugby concrétise une telle forme.

Sommaire

Représentation

En géométrie cartésienne, une sphère de centre (x0,y0,z0) et de rayon r est l'ensemble des points (x,y,z) tels que :

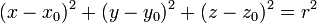\displaystyle (x-x_0)^2+(y-y_0)^2+(z-z_0)^2 = r^2.

Les points de la sphère de rayon r et de centre l'origine du repère peuvent être paramétrés par :

\left\{ \begin{matrix} x & = & r \cos\theta \; \cos\phi \\ y & = & r \cos\theta \; \sin\phi \\ z & = & r \sin\theta \end{matrix} \right. \qquad (\frac{-\pi}{2} \le\theta\le \frac{\pi}{2} \mbox{ et } -\pi \le \phi \le \pi)

On peut voir 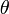\displaystyle \theta comme la latitude et 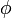\displaystyle \phi comme la longitude. (Voir fonctions trigonométriques et coordonnées sphériques.)

Formules

La surface d'une sphère de rayon r est :

S=4 \pi r^{2} \,

Le volume qu'elle renferme est :

V= \frac{4 \pi r^{3}}{3}

Sa compacité est de :

C= \frac{S}{V}= \frac {3}{r}

Le moment d'inertie d'une sphère homogène pleine de rayon R, de masse volumique ρ, de masse M par rapport à un axe passant par son centre est:

I=\frac{2 M R^2}{5}=\frac{8 \pi \rho R^5}{15}

Le moment d'inertie d'une sphère homogène vide de rayon R, de masse M par rapport à un axe passant par son centre est :

I=\frac{2 M R^2}{3}=\frac{8 \pi \rho R^5}{9}

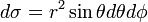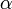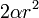L'élément d'aire de la sphère de rayon r\, dans les coordonnées latitude-longitude est d\sigma=r^2\sin\theta d\theta d\phi\,. On en déduit que l'aire d'un fuseau (portion limitée par deux demi-cercles joignant les pôles et faisant un angle \alpha\, exprimé en radians) est 2\alpha r^2\,.

Cela permet aussi de calculer l'aire d'une calotte sphérique (on dit aussi segment de sphère), c’est-à-dire d'une portion de sphère limitée par deux plans parallèles de distance 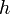h\, l'un pouvant être tangent à la sphère. On trouve 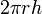2\pi rh\, : l'aire est la même que celle d'un cylindre circulaire de même hauteur tangent à la sphère (cylindre circonscrit). Ce résultat remarquable était connu d'Archimède, qui aurait demandé qu'il soit mentionné sur son tombeau.

Le cylindre circonscrit à une sphère donnée a un volume égal à 3⁄2 fois le volume de la sphère.

La sphère a la plus petite aire parmi les surfaces renfermant un volume donné et renferme le volume le plus élevé parmi les surfaces d'une aire donnée. Elle est la réponse à la question d'isopérimétrie pour l'espace euclidien de dimension 3. Pour cette raison, la sphère apparaît dans la nature, par exemple les bulles et gouttes d'eau (en l'absence de gravité) sont des sphères car la tension superficielle essaie de minimiser l'aire.

Développement

On peut démontrer que la sphère est une surface non développable. Il n'existe pas de patron de la sphère. Néanmoins, il est possible en pratique, d'obtenir des surfaces développables approchant la sphère très fidèlement, c'est le cas de tous les ballons cousus. Voir : Ballon de football (icosaèdre tronqué), ballon de Volley Ball, et ballon fantaisie (en fuseaux de pôle à pôle.)

Notez que la pression interne gauchit les surfaces et fidélise l'approche… Plus on gonfle plus la sphère est parfaite.

Généralisation aux autres dimensions

On peut généraliser le concept de sphère à un espace de dimension quelconque dans N. Pour tout entier naturel n, une n-sphere, notée Sn, est l'ensemble des points de l'espace euclidien à (n+1) dimensions qui sont à distance fixée r d'un point de cet espace (r est un réel strictement positif). Par exemple :

  • une 0-sphère est la paire des points extrémités de l'intervalle (−r, r) de la ligne réelle,
  • une 1-sphère est un cercle de rayon r
  • une 2-sphère est une sphère ordinaire

Les sphères de dimension n > 2 sont parfois appelées hypersphères.

L'aire d'une (n−1)-sphère de rayon 1 est

2 \frac{\pi^{n/2}}{\Gamma(n/2)}

où Γ(z) est la fonction Gamma d'Euler.

Une autre formule pour la surface est

\begin{cases} \displaystyle \frac{(2\pi)^{n/2}\,r^{n-1}}{2 \cdot 4 \cdots (n-2)} , & \text{si } n \text{ est pair ;} \\ \\ \displaystyle \frac{2(2\pi)^{(n-1)/2}\,r^{n-1}}{1 \cdot 3 \cdots (n-2)} , & \text{si } n \text{ est impair}. \end{cases}

et le volume intérieur est l'aire multipliée par 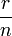{r \over n} ou

\begin{cases} \displaystyle \frac{(2\pi)^{n/2}\,r^n}{2 \cdot 4 \cdots n} , & \text{si } n \text{ est pair ;} \\ \\ \displaystyle \frac{2(2\pi)^{(n-1)/2}\,r^n}{1 \cdot 3 \cdots n} , & \text{si } n \text{ est impair}. \end{cases}

On notera au passage que la caractéristique d'Euler d'une n − sphere vaut

\begin{cases} \displaystyle 2 , & \text{si } n \text{ est pair ;} \\ \\ \displaystyle 0 , & \text{si } n \text{ est impair}. \end{cases}

Voir aussi

  • D. Hilbert et S. Cohn-Vossen, Geometry and imagination, Chelsea 1952
  • B. Berger, Géométrie (chap. 18), Nathan 1990, (ISBN 209-191-730-3)

Notes et références

  1. ↑ Le terme « géosphère » serait utilisé en ce sens en astrophysique et en architecture.
  2. ↑ Voir « géosphère » dans le Trésor de la langue française informatisé.

Articles connexes

Liens externes


Solides géométriques
Les polyèdres
Les solides de Platon
Tétraèdre - Cube - Octaèdre - Icosaèdre - Dodécaèdre
Les solides d'Archimède
Tétraèdre tronqué - Cube tronqué - Octaèdre tronqué - Dodécaèdre tronqué - Icosaèdre tronqué - Cuboctaèdre - Cube adouci - Icosidodécaèdre - Dodécaèdre adouci - Petit rhombicuboctaèdre - Grand rhombicuboctaèdre - Petit rhombicosidodécaèdre - Grand rhombicosidodécaèdre
Les solides de Kepler-Poinsot
Petit dodécaèdre étoilé - Grand dodécaèdre étoilé - Grand dodécaèdre - Grand icosaèdre
Les solides de Catalan
Triakioctaèdre - Tétrakihexaèdre - Triakitétraèdre - Pentakidodécaèdre - Triaki-icosaèdre - Dodécaèdre rhombique - Icositétraèdre pentagonal - Triacontaèdre rhombique - Hexacontaèdre pentagonal - Icositétraèdre trapézoïdal - Hexakioctaèdre - Hexacontaèdre trapézoïdal - Hexaki icosaèdre
Les solides de Johnson
Les solides de révolution
Boule - Cylindre de révolution - Cône de révolution - Tore - Paraboloïde de révolution
  • Portail de la géométrie Portail de la géométrie
Ce document provient de « Sph%C3%A8re ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Sphères de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

  • Spheres — Студийный альбом Pestilence Дата …   Википедия

  • Spheres — Álbum de Pestilence Publicación 1993 Grabación 1993 en Studio Arnold Mühren Género(s) Death metal técnico Metal progresivo …   Wikipedia Español

  • spheres — spheres. См. сферы. (Источник: «Англо русский толковый словарь генетических терминов». Арефьев В.А., Лисовенко Л.А., Москва: Изд во ВНИРО, 1995 г.) …   Молекулярная биология и генетика. Толковый словарь.

  • SPHERES — The Synchronized Position Hold, Engage, Reorient Experimental Satellites (SPHERES) experiment is a testbed consisting of three 8 inch diameter miniaturized satellites that can operate in a variety of environments, including inside the… …   Wikipedia

  • Spheres 2 — Infobox Album Name = Spheres 2 Type = studio Artist = Delerium Released = 1994 Recorded = Genre = Electronic Length = Label = Producer = Bill Leeb, Rhys Fulber Reviews = Last album = This album = Next album = Spheres 2 is an album by Canadian… …   Wikipedia

  • Sphères (Sloterdijk) — Sphères (Peter Sloterdijk) Pour les articles homonymes, voir Sphère (homonymie). Sphères (Sphären) est une trilogie du philosophe allemand Peter Sloterdijk publiée chez Suhrkamp Verlag dont les trois tomes sont parus respectivement en 1998… …   Wikipédia en Français

  • Spheres of Justice — Spheres of Justice: a defense of pluralism and equality (deutsch: Sphären der Gerechtigkeit. Ein Plädoyer für Pluralität und Gleichheit ) ist ein Werk des Philosophen Michael Walzer aus dem Jahr 1983. Walzer gilt als ein Vertreter des… …   Deutsch Wikipedia

  • Spheres of Justice — Spheres of Justice, with the subtitle In defence of pluralism and equality , is the title of a book written by Michael Walzer (ISBN 0 465 08189 4). In it, Walzer argues in favour of an idea he calls complex equality , and against the view that… …   Wikipedia

  • Spheres (TV series) — articleissues expand = August 2008 unreferenced = August 2008 tooshort = August 2008Infobox Television show name = Spheres caption = show name 2 = genre = Animated television series creator = writer = director = Byeon Yeong Kyoo creat director =… …   Wikipedia

  • Sphères (Peter Sloterdijk) — Pour les articles homonymes, voir Sphère (homonymie). Sphères (Sphären) est une trilogie du philosophe allemand Peter Sloterdijk publiée chez Suhrkamp Verlag dont les trois tomes sont parus respectivement en 1998 (Blasen ;… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”