Compacite (mathematiques)

Compacite (mathematiques): Compacité (mathématiques)

Pour les articles homonymes, voir Compacité et Compact.

En topologie de la droite réelle, la propriété de Borel-Lebesgue est une propriété topologique remarquable des segments, basée sur la notion de recouvrement. Elle sert d'axiome en topologie générale pour définir la notion d'espace compact, et étendre plusieurs des résultats concernant les segments à un cadre très général. Le nom choisi pour cet axiome rend hommage aux mathématiciens français Émile Borel et Henri Lebesgue.

Sommaire

1 Propriété de Borel-Lebesgue

2 Axiome de Borel-Lebesgue et définition générale des compacts

3 Définition par la théorie des filtres

4 Propriétés

4.1 Compacts et fermés

4.2 Autres propriétés

4.3 Compacité et continuité

4.4 Théorème de Bolzano-Weierstrass et compacité séquentielle

5 Exemples

Propriété de Borel-Lebesgue

Définition préalable : Soit E un ensemble, et A une partie de E. On dit qu'une famille 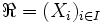$\Re = (X_i )_{i \in I}$ de parties de E recouvre A si leur réunion 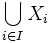$\bigcup\limits_{i \in I} {X_i }$ contient A

Propriété de Borel-Lebesgue pour les segments : soit un segment [a,b] de la droite réelle. De tout recouvrement de ce segment par des ouverts, on peut extraire un sous-recouvrement fini. C'est-à-dire que pour toute famille 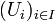$(U_i )_{i \in I}$ d'ensembles ouverts recouvrant [a,b], il existe une partie finie J de I telle que la sous-famille 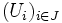$(U_i )_{i \in J}$ recouvre [a,b].

Pour une démonstration de cette propriété voir le théorème de Borel-Lebesgue, aussi appelé théorème de Heine-Borel.

La propriété de Borel-Lebesgue est étroitement liée à une propriété des suites bornées de réels : de toute suite bornée de réels, on peut extraire une suite convergente. Le lien entre les deux propriétés apparaîtra plus nettement dans la section suivante.

De l'une ou l'autre de ces propriétés il est possible de tirer quelques conséquences importantes sur les fonctions numériques. Notamment : l'image d'un segment par une application continue est un segment, et la fonction est alors uniformément continue (théorème de Heine).

Axiome de Borel-Lebesgue et définition générale des compacts

Un espace topologique E est dit quasi-compact s'il vérifie l'axiome de Borel-Lebesgue : de tout recouvrement ouvert de E, on peut extraire un sous-recouvrement fini. L'espace est dit compact quand il est en outre séparé.

Par passage au complémentaire, cette dernière propriété est équivalente à la propriété suivante : si 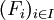$(F_i)_{i\in I}$ est une famille de fermés telle que 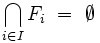$\bigcap_{i\in I}F_i\ =\ \empty$ , alors on peut extraire une famille finie 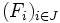$(F_i)_{i\in J}$ , avec 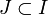$J \subset I$ , telle que 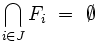$\bigcap_{i\in J}F_i\ =\ \empty$ . Ou encore, par contraposition, si toute intersection finie 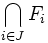$\bigcap_{i\in J}F_i$ d'une famille de fermés est non vide, alors l'intersection 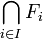$\bigcap_{i\in I}F_i$ de toute la famille est non vide.

NB : En terminologie anglo-saxonne, la définition est légèrement différente. Sauf mention contraire, le compact anglophone est un quasi-compact francophone, et la notion de quasi-compacité n'existe pas. Toutes les propriétés ne s'appliquent donc pas en général, sauf sous l'hypothèse que l'espace est séparé ("Hausdorff space")

Définition par la théorie des filtres

Un espace topologique séparé est compact ssi pour tout filtre F sur E, il existe un filtre plus fin que F qui converge ou encore ssi tout ultrafiltre sur E converge.

Propriétés

Compacts et fermés

Toute partie compacte d'un espace topologique séparé est fermée.

Preuve directe :
On suppose que x appartient au complémentaire de A dans E et on démontre qu'il existe un ouvert contenant x dont l'intersection avec A est vide. Ainsi ce complémentaire est ouvert et donc A est fermé :

Soit 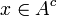$x \in A^c$ . E étant séparé, pour tout 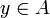$y \in A$ il existe un ouvert $O y$ contenant y et un ouvert $O x (y)$ (dépendant du choix de $O y$ ) contenant x tel que 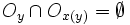$O_y \cap O_{x(y)}=\emptyset$ . La réunion 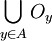$\bigcup_{y\in A}O_y$ de tels ouverts est un recouvrement de A par une famille d'ouverts. On peut donc en extraire un recouvrement fini de A: 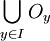$\bigcup_{y\in I}O_y$ , I étant un sous ensemble fini de A. Alors pour tout 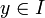$y \in I$ les implications successives :
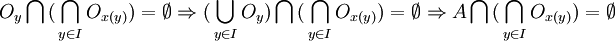
$\displaystyle{O_y \bigcap \big (\bigcap_{y\in I}O_{x(y)}\big)=\emptyset\Rightarrow \big(\bigcup_{y \in I} O_y\big)\bigcap \big (\bigcap_{y\in I}O_{x(y)}\big)=\emptyset\Rightarrow A \bigcap \big(\bigcap_{y\in I}O_{x(y)}\big)=\emptyset}$
prouvent que l'ouvert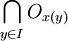 $\bigcap_{y \in I} O_{x(y)}$ contenant x possède une intersection vide avec A. Ainsi $A c$ est ouvert et A est donc fermé.

Preuve par contraposition :

Soit A un espace compact, mais non fermé:
Il existe alors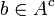 $b\in A^c$ tel que chacun de ses voisinages coupe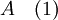 $A \quad (1)$
Soit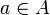 $a\in A$ : $a, b$ ont deux voisinages disjoints $O a, V b (a)$ ; la topologie étant séparée,
L'ensemble des $O a$ est un recouvrement ouvert de A.
Par compacité,on peut en extraire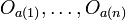 $O_{a(1)},\dots,O_{a(n)}$ un recouvrement fini de A.
D'une part, l'intersection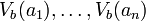 $V_b(a_1),\dots,V_b(a_n)$ étant ouverte, elle coupe $A$ , d'après $(1)$
D'autre part, elle ne coupe aucun des $O a (i)$ : à fortiri, elle ne coupe pas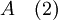 $A \quad (2)$
De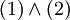 $(1)\land (2)$ ,on obtient bien la contradiction souhaitée.

NB: Ceci est en général faux si l'espace ambiant n'est pas séparé ; par exemple dans $\R$ munie de la topologie grossière 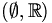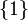$(\empty,\R)$ , $\left\{ 1 \right\}$ est compact mais pas fermé.

Toute partie fermée d'un espace compact est compacte

Soit $C$ un espace compact, $F$ une partie fermée de $C$ , et 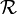$\mathcal{R}$ un recouvrement ouvert de $F$ . Si l'on adjoint à 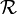$\mathcal{R}$ l'ensemble ouvert $C - F$ , on obtient un recouvrement ouvert 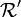$\mathcal{R}'$ de $C$ . Puisque $C$ est compact, on peut extraire de 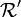$\mathcal{R}'$ un recouvrement fini 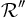$\mathcal{R}''$ de $C$ . Comme 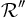$\mathcal{R}''$ est un recouvrement de $C$ c'est aussi un recouvrement de $F$ . Hormis l'éventuel ensemble $C - F$ , tous les membres de 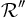$\mathcal{R}''$ sont par construction membres de $\mathcal{R}$ , recouvrement d'origine de $F$ . En en enlevant $C - F$ , qui ne contribue pas à recouvrir $F$ , on obtient un recouvrement fini de $F$ extrait du recouvrement d'origine $\mathcal{R}$ .

Un espace compact est normal

Un espace est dit normal si, pour tout coupe de fermés disjoints A et B il existe deux ouverts disjoints O_A et O_B, tel que l'intersection des deux ouverts soit nul. Ce type de propriété est utilisé, par exemple, pour énoncer le lemme d'Urysohn. La démonstration est donnée dans l'article espace normal.

Autres propriétés

Les compacts de l'ensemble des nombres réels, muni de sa topologie usuelle, sont les fermés bornés

Ce résultat est connu sous le nom de théorème de Borel-Lebesgue.

Le produit cartésien de compacts, munis de la topologie produit est compact

Ce résultat est connu sous le nom de théorème de Tychonov.

Dans un espace vectoriel de dimension finie sur le corps des réels ou des complexes, les compacts sont les fermés bornés

Cette question est traitée dans l'article topologie d'un espace vectoriel de dimension finie. Le caractère fini de la dimension est primordial. On démontre en effet que la boule unité centrée en 0 et de rayon 1 n'est pas compact dans un espace qui n'est pas de dimension finie. Ce résultat est connu sous le nom de théorème de Riesz.

Compacité et continuité

Une fonction à valeurs réelles continue sur un compact atteint toujours son maximum.

L'image d'un compact C par une application continue f est compact si l'ensemble d'arrivée est séparé.

Considérons un recouvrement ouvert de f(C), son image réciproque par f est un recouvrement ouvert de C. On peut en extraire un sous-recouvrement fini, l'image par f de ce sous-recouvrement est un sous-recouvrement de C extrait du recouvrement initial. L'existence d'un tel sous-recouvrement démontre la compacité de f(C).

Un premier exemple d'usage de ce résultat est le théorème des bornes, stipulant que l'image d'un segment par une application de R dans R, ici R désigne l'ensemble des réels, atteint ses bornes.

Un deuxième exemple est la démonstration du caractère isopérimétrique d'un polygone régulier, question ouverte depuis l'antiquité. L'objet est de savoir quel est le polygone à n côtés qui possède la plus grande aire, pour un périmètre donné. Des raisonnements géométriques assez simples montrent que l'unique candidat possible est le polygone régulier, résultat démontré depuis l'antiquité grecque. En revanche, l'existence d'une solution à cette question est restée ouverte jusqu'au XIX^e siècle.

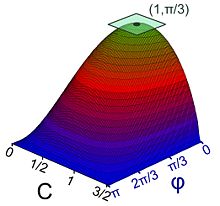
Pour comprendre la nature de la démonstration, le plus simple est de considérer le cas du triangle, illustré sur la figure de droite. Les triangles considérés sont tous de périmètre 3, ils sont identifiés à un couple (c, φ) où c désigne la longueur d'un coté et φ l'angle entre deux cotés dont l'un est celui de longueur c. La fonction f est celle qui, à un couple, associe la surface du triangle. Il n'est nécessaire que d'étudier la zone où c est compris entre 0 et 3/2 et φ entre 0 et π. Cette zone est un compact de R². L'application f est continue, elle atteint donc son maximum, en l'occurrence au point (1, π/3). L'existence de ce maximum était le chaînon manquant pour une démonstration complète.

Pour le triangle, un peu d'analyse permet tout aussi bien de démontrer le résultat. Pour le cas général du polygone à n côtés, il n'est pas bien difficile de construire une démonstration analogue à celle présentée ici, grâce à la notion de compact. La solution analytique est en revanche vraiment lourde. Une démonstration détaillée est présentée dans l'article théorème isopérimétrique.

Théorème de Bolzano-Weierstrass et compacité séquentielle

Article détaillé : théorème de Bolzano-Weierstrass.

Dans le cadre des espaces métriques (automatiquement séparés), le théorème de Bolzano-Weierstrass énonce qu'un espace K est compact si et seulement si de toute suite d'éléments de K il est possible d'extraire une sous-suite qui converge vers un élément de K, ou, de manière équivalente, toute suite admet une valeur d'adhérence.

Pour cette raison, dans le cadre des espaces métriques, la propriété de compacité est fréquemment introduite par caractérisation séquentielle.

Exemples

Tout espace fini séparé est compact. Chaque point est en effet recouvert par un ouvert, le sous-recouvrement comportant un ouvert par point est fini, ce qui montre la compacité.

L'ensemble constitué des images d'une suite convergente ainsi que de la limite dans un espace séparé est compact. En effet, de tout recouvrement ouvert, on peut extraire un ouvert contenant la limite, comme il n'existe qu'un nombre de points fini hors de cet ouvert, il est aisé de trouver un sous-recouvrement fini.

Portail des mathématiques

Ce document provient de « Compacit%C3%A9 (math%C3%A9matiques) ».

Catégorie : Compacité

Contenu soumis à la licence CC-BY-SA. Source : Article Compacite (mathematiques) de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

Compacité (Mathématiques) — Pour les articles homonymes, voir Compacité et Compact. En topologie de la droite réelle, la propriété de Borel Lebesgue est une propriété topologique remarquable des segments, basée sur la notion de recouvrement. Elle sert d axiome en topologie… … Wikipédia en Français
Compacité (mathématiques) — Pour les articles homonymes, voir Compacité et Compact. En topologie, on dit d un espace séparé qu il est compact, ou qu il vérifie la propriété de Borel Lebesgue, si chaque fois qu il est recouvert par des ouverts, il est recouvert par un nombre … Wikipédia en Français
Compacite sequentielle — Compacité séquentielle Pour les articles homonymes, voir Compacité. La compacité est une propriété topologique importante qui se définit en topologie générale, à partir de la notion de recouvrement ouvert. Toutefois dans le cadre des espaces… … Wikipédia en Français
Compacité Séquentielle — Pour les articles homonymes, voir Compacité. La compacité est une propriété topologique importante qui se définit en topologie générale, à partir de la notion de recouvrement ouvert. Toutefois dans le cadre des espaces métriques (comprenant… … Wikipédia en Français
Compacite — Compacité Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. La compacité est le caractère de ce qui est compact. Ce terme prend un sens particulier dans certains domaines : en topologie… … Wikipédia en Français
Compacité séquentielle — Pour les articles homonymes, voir Compacité. La compacité est une propriété topologique importante qui se définit en topologie générale, à partir de la notion de recouvrement ouvert. Toutefois dans le cadre des espaces métriques (comprenant… … Wikipédia en Français
Compacité — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. La compacité est le caractère de ce qui est compact. Ce terme prend un sens particulier dans certains domaines : en topologie (mathématiques), voir… … Wikipédia en Français
Quasi-compacité — Compacité (mathématiques) Pour les articles homonymes, voir Compacité et Compact. En topologie de la droite réelle, la propriété de Borel Lebesgue est une propriété topologique remarquable des segments, basée sur la notion de recouvrement. Elle… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français

Mark and share
Search through all dictionaries
Translate…
Search Internet

Share the article and excerpts