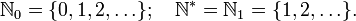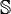Nombre entier naturel

Nombre entier naturel

Entier naturel

Page d'aide sur l'homonymie Pour les articles homonymes, voir Entier (homonymie).
Les entiers naturels permettent de compter (une pomme, deux pommes, trois pommes...).

Un entier naturel, aussi appelé nombre naturel, est un nombre entier et positif.

Ce sont des nombres qui permettent de compter les objets quand ils sont en quantité discrète ; par exemple, les doigts, les feuilles d'un arbre. Ils ne permettent pas de mesurer des quantités continues comme une longueur, un volume ou une masse.

L'idée de considérer zéro comme un entier naturel est relativement récente.

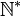Bien que cette notion paraisse intuitive, leur définition formelle en mathématiques n'a pas été simple à concrétiser. Les axiomes de Peano définissent l'ensemble des entiers naturels, noté N ou \mathbb{N}. On note \mathbb{N}^* l'ensemble des entiers naturels privé de l'élément zéro.

Sommaire

Notation

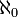Les mathématiciens utilisent N ou \mathbb{N} (un N en blackboard gras) pour décrire l'ensemble de tous les entiers naturels. Cet ensemble est infini mais, par définition, dénombrable. Cela revient à dire que le nombre cardinal de l'ensemble \mathbb{N} est aleph-zéro, noté \aleph_0.

Pour lever l'ambiguïté au sujet de l'inclusion du zéro dans l'ensemble ou non, on ajoute parfois un indice 0 sur le N quand le zéro est inclus. On ajoute quelques fois un indice 1 ou une astérisque sur celui-ci quand le zéro est exclus.

\mathbb{N}_0 = \{ 0, 1, 2, \ldots \}; \quad \mathbb{N}^* = \mathbb{N}_1 = \{ 1, 2, \ldots \}.

Plusieurs mathématiciens notent l'ensemble des entiers naturels incluant le zéro par la lettre minuscule grecque oméga : ω. Cette situation découle de l'identification d'un nombre ordinal avec l'ensemble des ordinaux qui sont plus petits.

Une abstraction des collections d'objets réels

La notion de collection d'objets ou d'animaux, par exemple des fruits ou un troupeau, est supposée avoir précédée celle du nombre. Ces objets n'ont rien à voir entre eux, mais ils ont pourtant une caractéristique commune : dans un panier, les tomates sont distinctes et à peu près identiques, dans un troupeau, les vaches sont elles aussi distinctes et à peu près identiques. Ce ou ces caractères communs définissent une collection.

Des objets abstraits furent inventés en se fondant sur la propriété suivante : ils sont distincts et interchangeables. Ces objets sont des unités. Euclide en donne au Livre VII la définition suivante : « L'unité est ce relativement à quoi tout objet est appelé Un. »

De cette notion fut extraite la propriété qui nous intéresse : la « dénombrabilité », et un objet idéal qui n'a que cette propriété, fut imaginé. Ce processus mental est connu sous le nom d'abstraction : il est fait abstraction de la qualité de l'objet pour s'intéresser uniquement à la quantité.

Euclide définit ainsi le nombre : « Le nombre est une collection d'unités ». Cette définition inclut implicitement le nombre zéro, une collection ne comprenant aucune unité.

Les entiers naturels peuvent aussi être définis par abstraction sans passer par la notion d'unité, comme l'a fait G. Frege (Fondements de l'arithmétique, 1884). Une collection A (ou concept selon sa terminologie) et une collection B sont dites équinumériques si on peut définir une correspondance biunivoque entre les objets de A et les objets de B, c'est-à-dire une correspondance qui associe à tout objet de A un unique objet de B, et à tout objet de B un unique objet de A. Un nombre est alors défini par abstraction des collections équinumériques entre elles, indépendamment de la nature de ces collections.

À chaque nombre est associé un symbole, ce qui permet de construire un ensemble d'objets différents les uns des autres.

Article détaillé : construction des entiers naturels.

Propriétés algébriques

Addition Multiplication
Clôture a + b   est un entier naturel a × b   est un entier naturel
Associativité a + (b + c)  =  (a + b) + c a × (b × c)  =  (a × b) × c
Commutativité a + b  =  b + a a × b  =  b × a
Existence d'un élément neutre a + 0  =  a a × 1  =  a
Distributivité a × (b + c)  =  (a × b) + (a × c)

Axiomes de Peano

Article détaillé : Axiomes de Peano.

Quelle que soit la façon d'introduire les entiers naturels, ceux-ci ont les mêmes propriétés fondamentales à partir desquelles on développe l'arithmétique. Les axiomes de Peano sont un ensemble d'axiomes de second ordre proposés par Giuseppe Peano pour définir l'arithmétique. Ils sont au nombre de cinq :

  1. l'élément appelé zéro et noté: 0, est un entier naturel.
  2. Tout entier naturel n a un unique successeur, noté s(n) ou Sn.
  3. Aucun entier naturel n'a 0 pour successeur.
  4. Deux entiers naturels ayant même successeur sont égaux.
  5. Si un ensemble d'entiers naturels contient 0 et contient le successeur de chacun de ses éléments, alors cet ensemble est égal à \mathbb{N}.

Le premier axiome permet de poser que l'ensemble des entiers naturels n'est pas vide, le troisième qu'il possède un premier élément et le cinquième qu'il vérifie le principe de récurrence.

Remarque

Les français appellent ces entiers, entiers positifs alors que dans le système anglo-saxon on les appellera entiers non négatifs (non negative integers), vu que dans ce système les entiers positifs sont ceux strictement supérieur à 0. Cela prête parfois à confusion.

Nombres figurés

Les nombres entiers non nuls peuvent être représentés graphiquement.

Article détaillé : Nombre figuré.
1 2 3 4 5 6 7 8 9 10
* ** *
**		 **
**		 *
***
*		 *
**
***		 **
***
**		 * ***
***
***		 *
**
***
****

Voir aussi

Sur les autres projets Wikimedia :

Articles connexes

Liens externes

Notion de nombre
Ensembles usuels \mathbb{N} Entier naturel • \mathbb{Z} Entier relatif • \mathbb{D} Nombre décimal • \mathbb{Q} Nombre rationnel • \mathbb{R} Nombre réel • \mathbb{C} Nombre complexe Mathématiques
Extensions \mathbb{H} Quaternion • \mathbb{O} Octonion • \mathbb{S} Sédénion • Nombre complexe fendu • Tessarine • Nombre bicomplexe • Nombre multicomplexe • Biquaternion • Coquaternion • Octonion fendu • Nombre hypercomplexe • \mathbb{Q}_p Nombre p-adique • Nombre hyperréel • Nombre superréel • Nombre dual • Droite réelle achevée • Nombre cardinal • Nombre ordinal • Nombre surréel et pseudo-réel
Propriétés particulières Parité • Nombre premier • Nombre composé • Carré parfait • Nombre parfait • Nombre positif • Nombre négatif • Fraction dyadique • Nombre irrationnel • Nombre algébrique • Nombre transcendant • Nombre imaginaire pur • Nombre de Liouville • Nombre normal • Nombre univers • Nombre constructible • Nombre réel calculable • Nombre transfini • Infiniment petit • Infiniment grand
Exemples d’importance historique π Pi • √2 Racine carrée de deux • φ Nombre d’or • 0 Zéro • i Unité imaginaire • e Constante de Neper • ℵ0 Aleph-zéro • Table de constantes mathématiques
Notions connexes Chiffre • Numération • Fraction • Opération • Calcul • Algèbre • Arithmétique • Suite d’entiers • ∞ Infini • Chiffre significatif


Ensembles d'entiers sur la base de leur divisibilité
Formes de factorisation : Nombre premier · Nombre composé · Nombre puissant · Entier sans facteur carré
Sommes de diviseurs : Nombre parfait · Nombre presque parfait · Nombre quasi parfait · Nombre parfait multiple · Nombre hyperparfait · Nombre parfait unitaire · Nombre semi-parfait · Nombre semi-parfait primitif · Nombre pratique
Nombres de diviseurs : Nombre abondant · Nombre hautement abondant · Nombre superabondant · Nombre colossalement abondant · Nombre hautement composé
Autres : Nombre déficient · Nombre étrange · Nombre amical · Nombre sociable · Nombre solitaire · Nombre sublime · Nombre à moyenne harmonique entière · Nombre frugal · Nombre équidigital · Nombre extravagant
  • Portail des mathématiques Portail des mathématiques

Ce document provient de « Entier naturel ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Nombre entier naturel de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Entier Naturel — Pour les articles homonymes, voir Entier (homonymie). Les entiers naturels permettent de compter (une pomme, deux pommes, trois pommes...). Un entier natur …   Wikipédia en Français

  • Entier naturel — Pour les articles homonymes, voir Entier (homonymie). En mathématiques, un entier naturel est un nombre positif ou nul permettant fondamentalement de dénombrer des objets comptant chacun pour un. Un tel nombre entier peut s écrire avec une suite… …   Wikipédia en Français

  • Nombre entier — Entier relatif Pour les articles homonymes, voir Entier (homonymie). En mathématiques, un entier relatif (ou entier rationnel) est un nombre entier (c est à dire sans partie fractionnaire) et muni d un signe positif ( + ) ou négatif ( − ). L… …   Wikipédia en Français

  • Nombre entier relatif — Entier relatif Pour les articles homonymes, voir Entier (homonymie). En mathématiques, un entier relatif (ou entier rationnel) est un nombre entier (c est à dire sans partie fractionnaire) et muni d un signe positif ( + ) ou négatif ( − ). L… …   Wikipédia en Français

  • Entier (nombre) — Entier naturel Pour les articles homonymes, voir Entier (homonymie). Les entiers naturels permettent de compter (une pomme, deux pommes, trois pommes...). Un entier natur …   Wikipédia en Français

  • Entier positif — Entier naturel Pour les articles homonymes, voir Entier (homonymie). Les entiers naturels permettent de compter (une pomme, deux pommes, trois pommes...). Un entier natur …   Wikipédia en Français

  • Nombre naturel — Entier naturel Pour les articles homonymes, voir Entier (homonymie). Les entiers naturels permettent de compter (une pomme, deux pommes, trois pommes...). Un entier natur …   Wikipédia en Français

  • nombre — [ nɔ̃br ] n. m. • déb. XIIe; lat. numerus I ♦ 1 ♦ Concept de base des mathématiques, une des notions fondamentales de l entendement que l on peut rapporter à d autres idées (de pluralité, d ensemble, de correspondance), mais non définir.… …   Encyclopédie Universelle

  • Nombre Transfini — Les nombres transfinis sont des nombres infinis découverts et explorés par le mathématicien Georg Cantor. Se basant sur ses résultats, il a introduit une sorte de hiérarchie dans l infini, en développant la théorie des ensembles. Sommaire 1… …   Wikipédia en Français

  • naturel — naturel, elle [ natyrɛl ] adj. et n. • 1119 jorz naturals « jour astronomique »; lat. naturalis I ♦ 1 ♦ Qui appartient à la nature d un être, d une chose. Caractères naturels. ♢ Vx Qui appartient à la nature d un lieu. ⇒ indigène. « Le faucon qui …   Encyclopédie Universelle

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”