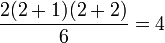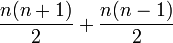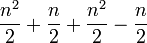Nombre Triangulaire

Nombre triangulaire

Un nombre triangulaire est un nombre qui peut être représenté par un triangle équilatéral. Les premiers termes de la suite des nombres triangulaires (A000217 dans l'encyclopédie électronique des suites entières) sont:

0, 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, ...

1
3
6
10
15

Puisque chaque ligne est d'une unité plus longue que la ligne précédente, nous pouvons remarquer qu'un nombre triangulaire est la somme de nombres entiers consécutifs.

Le nombre triangulaire de rang n est égal à

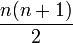$\frac{n(n + 1)}{2}\,$ ou

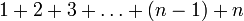$1+2+3+\ldots+(n-1)+n$ .

On reconnaît le coefficient binomial $C_{n+1}^2$ .

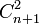Sommaire

1 Généralisation à la dimension n quelconque
2 Nombres triangulaires à 3 chiffres identiques
3 Propriétés générales
4 Voyez également

Généralisation à la dimension n quelconque

Il est possible également de démontrer que pour tout simplexe de dimension n ayant des côtés de longueur x, le nombre de points qui composent le simplexe est égal à

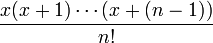$\frac {x(x+1)\cdots(x+(n-1))} {n!}$ .

Par exemple, un tétraèdre ayant des côtés de longueur 2 comprend un nombre total de

$\frac{2(2 + 1)(2 + 2)}{6}=4$

points. Les quatre points formant cette configuration sont les sommets du tétraèdre. Remarquons qu'un tétraèdre peut être créé en considérant un nombre et en formant le triangle de rang ce nombre, puis en lui adjoignant tous les triangles de rang inférieur à celui-ci. Ainsi un tétraèdre de rang 2 peut se construire à partir d'un triangle de rang 2 contenant 3 points et d'un triangle de rang ayant 1 point. Ce tétraèdre comprendra au total 4 points.

Nombres triangulaires à 3 chiffres identiques

L'un des nombres triangulaires les plus célèbres est 666 obtenu pour n = 36, également connu sous le nom de nombre de la bête. D'ailleurs 6 et 66 sont aussi triangulaires - obtenus pour n respectivement égal à 3, 11 - mais pas 6666 !

On peut généraliser le cas de 6 et 666 à toute base de la forme b = 3k+1 (k entier > 0). Au lieu de 6, on prend t = k(k+1)/2: alors T = t(b²+b+1) est aussi triangulaire, car T = m(m+1)/2 avec m = 6t. [Preuve: m(m+1)/2 = 3t(6t+1) et 3(6t+1) = 3(3k(k+1)+1) = 3((b-1)(b+2)/3 + 1) = (b-1)(b+2) + 3 = b²+b+1.] Ainsi, par exemple: en base 7, :3: et :333: sont triangulaires -> en décimal: 3 et 171; et en base 16, :F: et :FFF: le sont aussi (F désignant le nombre 15 en base 16) -> en déc.: 15 et 4095 (= 2¹² - 1). Cela s'applique aux valeurs 4,7,10,13,16 de b; dès b=19, t devient > b, de sorte que :t: et :ttt: ne sont plus des représentations d'entiers en base b normales ... (Dans ces exemples, les nombres notés :xyz: sont à considérer dans la base indiquée différente de 10.)

Propriétés générales

Tout nombre parfait pair est triangulaire. (Et on ignore toujours s'il existe un nombre parfait impair.)

La somme de deux nombres triangulaires consécutifs est un nombre carré. Ceci peut être démontré de la façon suivante:

la somme des nombres triangulaires de rang n et n-1 est égale à

$\frac{n(n+1)}{2}+\frac{n(n-1)}{2}$

qui se développe en

$\frac{n^2}{2}+\frac{n}{2}+\frac{n^2}{2}-\frac{n}{2}$

et se simplifie en n².

Cependant, il est possible de retrouver schématiquement ce résultat :

16
25

Dans chacun des exemples ci-dessus, un carré est formé de deux triangles juxtaposés.

En outre, le carré d'un nombre triangulaire de rang n est égale à la somme des cubes des entiers naturels de 1 à n. Cette représentation d'un nombre à l'aide de concept issue de la géométrie élémentaire est très fréquente à la naissance de l'algèbre, on appelle cette branche des mathématiques, l'algèbre géométrique. L'article associé montre comment calculer à l'aide de cette approche la somme des cubes.

En base 10, le résidu d'un nombre triangulaire est toujours égal à 1, 3, 6 ou 9. Par conséquent chaque nombre triangulaire est ou bien divisible par trois ou bien a un reste égal à 1 une fois divisé par neuf.

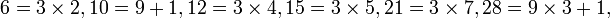$6=3 \times 2, 10=9+1, 12=3 \times 4, 15=3 \times 5, 21=3 \times 7, 28=9 \times 3+1,$ …

Les nombres triangulaires vérifient toutes sortes de relations avec d'autres nombres figurés, y compris avec des nombres figurés centrés. Toutes les fois qu'un nombre triangulaire est divisible par 3, le tiers de ce nombre est un nombre pentagonal. Tout autre nombre triangulaire est un nombre hexagonal. Un nombre hexagonal centré est égal à un nombre triangulaire multiplié par 6 plus 1. Un nombre carré centré est un nombre triangulaire multiplié par 4, plus 1.

Voyez également

Portail des mathématiques

Ce document provient de « Nombre triangulaire ».

Catégorie : Nombre figuré

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Nombre Triangulaire de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

Nombre triangulaire — Cette figure illustre le fait de 28 est le septième nombre triangulaire. En arithmétique, un nombre triangulaire est un cas particulier de nombre figuré. Il correspond à un nombre entier positif égal au nombre de pastilles dans un triangle… … Wikipédia en Français
Nombre Triangulaire Centré — Un nombre triangulaire centré est un nombre figuré centré qui peut être représenté par un triangle avec un point placé en son centre et tous les autres points disposés autour de ce centre. Le nombre triangulaire centré de rang n est égal à L… … Wikipédia en Français
Nombre triangulaire centre — Nombre triangulaire centré Un nombre triangulaire centré est un nombre figuré centré qui peut être représenté par un triangle avec un point placé en son centre et tous les autres points disposés autour de ce centre. Le nombre triangulaire centré… … Wikipédia en Français
Nombre triangulaire centré — Un nombre triangulaire centré est un nombre figuré centré qui peut être représenté par un triangle avec un point placé en son centre et tous les autres points disposés autour de ce centre. Le nombre triangulaire centré de rang n est égal à L… … Wikipédia en Français
Nombre Carré Triangulaire — Un nombre carré triangulaire est un nombre qui est à la fois un nombre triangulaire et un nombre carré. Il y a une infinité de nombres carrés triangulaires, qui s écrivent sous la forme . Le problème de la recherche des nombres carrés… … Wikipédia en Français
Nombre carre triangulaire — Nombre carré triangulaire Un nombre carré triangulaire est un nombre qui est à la fois un nombre triangulaire et un nombre carré. Il y a une infinité de nombres carrés triangulaires, qui s écrivent sous la forme . Le problème de la recherche des… … Wikipédia en Français
Nombre Centré — En mathématiques, les nombres centrés sont une classe des suites de nombres figurés, chacun formés par un point central, entouré par des couches polygonales successives constituées d un nombre constant de côtés. Chaque côté d une couche… … Wikipédia en Français
Nombre Polygonal Centré — Un nombre polygonal centré est un type de nombre figuré, qui peut être représenté par une figure plane ayant un point placé en son centre et tous les autres points disposés autour de ce centre formant des couches polygonales successives avec un… … Wikipédia en Français
Nombre centre — Nombre centré En mathématiques, les nombres centrés sont une classe des suites de nombres figurés, chacun formés par un point central, entouré par des couches polygonales successives constituées d un nombre constant de côtés. Chaque côté d une… … Wikipédia en Français
Nombre polygonal centre — Nombre polygonal centré Un nombre polygonal centré est un type de nombre figuré, qui peut être représenté par une figure plane ayant un point placé en son centre et tous les autres points disposés autour de ce centre formant des couches… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Nombre Triangulaire