Nombre Sociable

Nombre Sociable

Nombre sociable

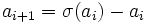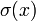En mathématiques, un nombre entier a est sociable d'ordre n si sa suite aliquote est fermée et compte n maillons. La formule de construction d'une chaîne aliquote est la suivante : a_{i+1} = \sigma(a_i) - a_i\,\! où \sigma(x)\,\! est la fonction donnant la somme des diviseurs entiers positifs de 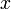x\,\!, incluant 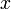x\,\! lui-même. Les nombres amicaux sont sociables d'ordre 2, les parfaits sociables d'ordre 1.

Le premier nombre sociable (d'ordre 5) fut découvert par P. Poulet, un mathématicien français, en 1918 : 12 496 → 14 288 → 15 472 → 14 536 → 14 264 (→ 12 496). En 1970, Henri Cohen, de Paris, en découvre sept d'ordre 4. On n'en connaît aucun d'ordre 3 ni 7.

La plus longue chaîne sociable 14 316 → 19 116 → 31 704 → 47 616 → 83 328 → 177 792 → 295 488 → 627 072 → 589 786 → 294 896 → 358 336 → 418 904 → 366 556 → 274 924 → 275 444 → 243 760 → 376 736 → 318 028 → 285 778 → 152 990 → 122 410 → 97 946 → 48 976 → 45 946 → 22 976 → 22 744 → 19 916 → 17 716 (→ 14 316) d'ordre 28 avait été découverte également par Poulet. Les ordinateurs n'ont depuis pas permis d'en découvrir d'autre que celle-là au-delà de l'ordre 9.

On en connaît seulement 2 d'ordre 6, 2 d'ordre 8 et 1 d'ordre 9. Par contre plus d'une centaine d'ordre 4.

Références

Voir aussi


Ensembles d'entiers sur la base de leur divisibilité
Formes de factorisation : Nombre premier · Nombre composé · Nombre puissant · Entier sans facteur carré
Sommes de diviseurs : Nombre parfait · Nombre presque parfait · Nombre quasi parfait · Nombre parfait multiple · Nombre hyperparfait · Nombre parfait unitaire · Nombre semi-parfait · Nombre semi-parfait primitif · Nombre pratique
Nombres de diviseurs : Nombre abondant · Nombre hautement abondant · Nombre superabondant · Nombre colossalement abondant · Nombre hautement composé
Autres : Nombre déficient · Nombre étrange · Nombre amical · Nombre sociable · Nombre solitaire · Nombre sublime · Nombre à moyenne harmonique entière · Nombre frugal · Nombre équidigital · Nombre extravagant
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Nombre sociable ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Nombre Sociable de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Nombre sociable — En mathématiques, un nombre entier a est sociable d ordre n si sa suite aliquote est fermée et compte n maillons. La formule de construction d une chaîne aliquote est la suivante : où est la fonction donnant la somme des diviseurs entiers… …   Wikipédia en Français

  • Nombre Parfait — Un nombre parfait est un nombre entier n strictement supérieur à 1 qui est égal à la somme de ses diviseurs stricts, autrement dit, tel que où σ(n) est la somme des diviseurs entiers positifs de n, n non compris. Le premier nombre parfait est 6,… …   Wikipédia en Français

  • Nombre Abondant — En mathématiques, un nombre abondant est un nombre entier naturel n qui est strictement inférieur à la somme de ses diviseurs stricts, autrement dit, tel que où est la somme des diviseurs entiers positifs de n y compris n. Les nombres abondants… …   Wikipédia en Français

  • Nombre Déficient — En mathématiques, un nombre déficient est un nombre entier naturel n qui est strictement supérieur à la somme de ses diviseurs stricts, autrement dit, tel que σ(n) < 2n où σ(n) est la somme des diviseurs entiers positifs de n y compris n . La… …   Wikipédia en Français

  • Nombre Presque Parfait — En mathématiques, un nombre presque parfait (quelquefois appelé aussi nombre légèrement déficient) est un entier naturel n tel que la somme de tous les diviseurs de n (ie. la fonction diviseur ) est égale à 2n 1. Les seuls nombres presque… …   Wikipédia en Français

  • Nombre Quasi Parfait — En mathématiques, un nombre quasi parfait est un entier n tel que . Où est la fonction donnant la somme des diviseurs entiers positifs de n, incluant n. Aucun nombre quasi parfait n a été trouvé jusqu à aujourd hui, mais il a été prouvé que si un …   Wikipédia en Français

  • Nombre aimable — Nombre amical En mathématiques et plus précisément en arithmétique modulaire, deux nombres entiers n et m sont dits amicaux ou aimables ou amiables si où est la fonction donnant la somme des diviseurs entiers positifs de , incluant lui même.… …   Wikipédia en Français

  • Nombre amiable — Nombre amical En mathématiques et plus précisément en arithmétique modulaire, deux nombres entiers n et m sont dits amicaux ou aimables ou amiables si où est la fonction donnant la somme des diviseurs entiers positifs de , incluant lui même.… …   Wikipédia en Français

  • Nombre deficient — Nombre déficient En mathématiques, un nombre déficient est un nombre entier naturel n qui est strictement supérieur à la somme de ses diviseurs stricts, autrement dit, tel que σ(n) < 2n où σ(n) est la somme des diviseurs entiers positifs de n… …   Wikipédia en Français

  • Nombre excessif — Nombre abondant En mathématiques, un nombre abondant est un nombre entier naturel n qui est strictement inférieur à la somme de ses diviseurs stricts, autrement dit, tel que où est la somme des diviseurs entiers positifs de n y compris n. Les… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”