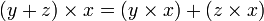Distributivite

Distributivite

Distributivité

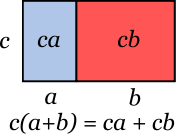
Dans un calcul faisant intervenir par exemple des nombres entiers ou réels, la distributivité permet de passer d'un produit de sommes à une somme de produit. Par exemple,

2x(5 + 3) = (2x5) + (2x3).

Le premier facteur 2 a été distribué à chacun des deux termes de la somme 5+3. On parle aussi de développement, l'opération inverse étant la factorisation. L'égalité est bien vérifiée dans ce cas particulier, à gauche 2x8 = 16, à droite 10+6 = 16, et se généralise aux nombres usuels (entiers ou non) : on dit que la multiplication y est distributive par rapport à l'addition.

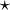Plus généralement, en algèbre on étudie des lois de composition internes sur les ensembles. L'addition et la multiplication des réels en sont des exemples. Une loi interne \circ est distributive par rapport à une autre loi interne \star dans un ensemble S si pour tous x, y, z dans S, on a les propriétés suivantes :

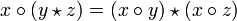x \circ ( y \star z ) = ( x \circ y ) \star ( x \circ z )   (Distributivité à droite) ;
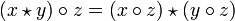( x \star y ) \circ z = ( x \circ z ) \star ( y \circ z )   (Distributivité à gauche).
Une illustration géométrique de la distributivité

Sommaire

Calcul élémentaire : les entiers

Si les facteurs d'un produit sont des sommes, on peut effectuer les produits terme à terme puis effectuer la somme : la multiplication est distributive par rapport à l'addition. Cette propriété intervient dans le calcul élémentaire.

Exemple.
235x99=235x(100-1)=23 500-235=23 265.

De même, la multiplication par les nombres uniformes 9, 99, 999, etc se ramène une soustraction en utilisant la distributivité.

Exemple.
458x592=(400+50+8)x(500+90+2)=200 000+36 000+800+25 000+4 500+100+4000+720+16=271 136.

Les algorithmes pour calculer effectivement un produit d'entiers utilisent fortement la distributivité. Elles reviennent à effectuer dans un ordre ou dans un autre la somme écrite ci-dessus.

Concept de nombre

La distributivité de la multiplication par rapport à l'addition, c'est-à-dire que pour tous x, y et z on a :

(y + z) \times x = (y \times x)+(z \times x)

qui est vérifiée pour les entiers, s'étend aux nombres rationnels aux nombres réels, et aux nombres complexes.

Par exemple, on montre, en utilisant entre autre la distributivité de la multiplication complexe, que (1 + i)2 = 1 + 2i + i2 = 2i, c'est-à-dire que (1 + i) est une racine carrée de 2i, et plus généralement, le produit de deux nombres complexes de la forme n+mi avec n et m entiers, que l'on appelle entiers de Gauss, est encore un entier de Gauss. Ce constat utilise la distributivité de la multiplication complexe.

Cette distributivité reste encore valable pour les quaternions de Hamilton, même si la multiplication n'est plus commutative.

Autre famille d'exemples : les quotients de Z héritent de l'addition et de la multiplication, et ces lois induites vérifient encore la distributivité.

Distributivité des lois binaires

Anneaux et corps.

La distributivité est une notion importante en algèbre et apparait dans de nombreuses définitions de structures, à commencer par les anneaux, les corps et les espaces vectoriels. Un anneau A est muni de deux lois binaires notées souvent + et x, telles que, entre autres, la loi x est distributive par rapport à +. Certaines identités remarquables, qui utilisent fortement la distributivité, utilisent également la commutativité. Elles ne sont pas généralement valides sur les anneaux non commutatifs, comme les anneaux de matrice.

Dans la définition d'un K-espace vectoriel E, la multiplication externe par des scalaires est distributive par rapport à l'addition des vecteurs. Ici, on a affaire à une loi externe et non une loi interne, mais le vocabulaire reste le même.

Treillis.

Sur l'ensemble 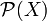\mathcal{P}(X) des parties de X, on dispose de deux lois binaires : la réunion 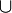\cup et l'intersection 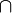\cap. Elles sont distributives l'une par rapport à l'autre. Explicitement :

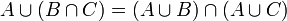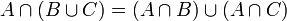A\cup (B\cap C)=(A\cup B)\cap (A\cup C) et A\cap (B\cup C)=(A\cap B)\cup (A\cap C).

La réunion 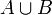A\cup B est la plus petite partie de X contenant A et B. Au contraire l'intersection 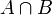A\cap B est la plus grande partie contenue dans A et B à la fois.

Plus généralement, un treillis est un ensemble partiellement ordonné S dans lequel toute partie finie admet un majorant et minorant. On note 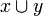x\cup y (join) et 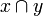x\cap y (meet) le majorant et le minorant de x et de y. Le treillis est dit distributif lorsque les deux lois sont distributives l'une par rapport à l'autre :

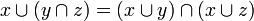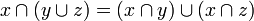x\cup (y\cap z)=(x\cup y)\cap (x\cup z) et x\cap (y\cup z)=(x\cap y)\cup (x\cap z).

Exemple de non distributivité

Les nombres ordinaux sont une généralisation à l'infini des entiers, qui sont les ordinaux finis, les entiers. La somme et le produit des entiers se généralisent naturellement à tous les ordinaux. Cependant, quand interviennent des ordinaux infinis, si le produit reste distributif à gauche par rapport à l'addition, il n'y a plus de distributivité à droite.

Voir aussi

Wiktprintable without text.svg

Voir « distributivité » sur le Wiktionnaire.
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Distributivit%C3%A9 ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Distributivite de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • distributivité — [ distribytivite ] n. f. • mil. XXe; de distributif ♦ Log., Math. Caractère d une opération, d une loi qui est distributive par rapport à une autre. ● distributivité nom féminin En mathématique, caractère d une loi de composition interne… …   Encyclopédie Universelle

  • Distributivité — Dans un calcul faisant intervenir par exemple des nombres entiers ou réels, la distributivité permet de passer d un produit de sommes à une somme de produit. Par exemple, 2x(5 + 3) = (2x5) + (2x3). Le premier facteur 2 a été distribué à chacun… …   Wikipédia en Français

  • Distributivite (mathematiques elementaires) — Distributivité (mathématiques élémentaires) Cet article fait partie de la série Mathématiques élémentaires Algèbre Logique Arithmétique Probabilités …   Wikipédia en Français

  • Distributivité (Mathématiques Élémentaires) — Cet article fait partie de la série Mathématiques élémentaires Algèbre Logique Arithmétique Probabilités …   Wikipédia en Français

  • Distributivité (maths élém) — Distributivité (mathématiques élémentaires) Cet article fait partie de la série Mathématiques élémentaires Algèbre Logique Arithmétique Probabilités …   Wikipédia en Français

  • Distributivité (mathématiques élémentaires) — La distributivité est une propriété de la multiplication qui permet d effectuer de deux manières différentes le produit d un nombre par une somme : Ici on a distribué a à chaque terme de la somme Ici on a distribué c à chaque terme de la… …   Wikipédia en Français

  • loi de distributivité — distributyvumo dėsnis statusas T sritis automatika atitikmenys: angl. distribution law; distributive law vok. distributives Gesetz, n; Verteilungsgesetz, n rus. дистрибутивный закон, m; распределительный закон, m pranc. loi de distributivité, f… …   Automatikos terminų žodynas

  • Distributive — Distributivité Dans un calcul faisant intervenir par exemple des nombres entiers ou réels, la distributivité permet de passer d un produit de sommes à une somme de produit. Par exemple, 2x(5 + 3) = (2x5) + (2x3). Le premier facteur 2 a été… …   Wikipédia en Français

  • Algèbre de Boole (structure) — Pour les articles homonymes, voir « Algèbre de Boole ». En mathématiques, une algèbre de Boole, ou parfois anneau de Boole, est une structure algébrique étudiée en particulier en logique mathématique. Une algèbre de Boole peut être… …   Wikipédia en Français

  • Algèbre des parties d'un ensemble — En théorie des ensembles, l ensemble des parties d un ensemble, muni des opérations d intersection, de réunion, et de passage au complémentaire possède une structure d algèbre de Boole. D autres opérations s en déduisent, comme la différence… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”