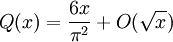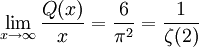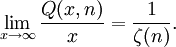Entier Sans Facteur Carré

Entier sans facteur carré

En mathématiques et plus précisément en arithmétique modulaire, un entier sans facteur carré est un entier divisible par aucun carré parfait, excepté 1. Par exemple, 10 est sans facteur carré mais 18 ne l'est pas, comme il est divisible par 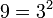$9 = 3^2\,$ . Les petits nombres sans facteur carré sont 1, 2, 3, 5, 6, 7, 10, 11, 13, 14, 15, 17, 19, 21, 22, 23, 26, 29, 30, 31, 33, ...

Caractérisation équivalente des nombres sans facteur carré

L'entier n est sans facteur carré si et seulement si dans la décomposition en facteurs premiers de n, aucun nombre premier n'apparait plus d'une fois. Un autre point de vue équivalent est que pour chaque diviseur premier p de n, le nombre premier p ne divise pas 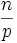$\frac{n}{p}\,$ . Une autre formulation est la suivante : n est sans facteur carré si et seulement si dans chaque décomposition n=ab, les facteurs a et b sont premiers entre eux.

Pour tout nombre premier p, la valuation p-adique de l'entier n est au plus égale à 1. On dit aussi parfois qu'un tel nombre est quadratfrei. On rappelle que pour tout nombre premier $p$ et tout entier naturel $n$ , la valuation $p$ -adique de $n$ (parfois notée $ν p (n)$ ) est égale, par définition, à l'exposant de $p$ dans la décomposition de $n$ en produit de nombres premiers.

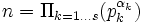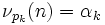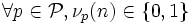Ainsi, si $n=\Pi_{k=1...s}(p_k^{\alpha_k})$ , on a $\nu_{p_k}(n)=\alpha_k$ , et $n$ est quadratfrei équivaut à $\forall p\in\mathcal P,\nu_p(n)\in \{ 0, 1 \}$ .

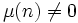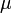L'entier naturel n est sans facteur carré si et seulement si $\mu(n) \ne 0\,$ , où $\mu\,$ représente la fonction de Möbius.

L'entier naturel n est sans facteur carré si et seulement si tous les groupes abéliens d'ordre n sont isomorphes, ce qui est le cas si et seulement si tous sont cycliques. Ceci découle du théorème de Kronecker.

L'entier naturel n est sans facteur carré si et seulement si l'anneau factoriel 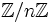$\mathbb{Z}/n\mathbb{Z}\,$ (voir Anneau Z/nZ) est un produit de corps. Ceci découle du théorème des restes chinois et le fait qu'un anneau de la forme 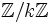$\mathbb{Z}/k\mathbb{Z}\,$ est un corps si et seulement si k est un nombre premier.

Pour chaque entier naturel n, l'ensemble de tous les diviseurs positifs de n devient un ensemble partiellement ordonné si nous utilisons la divisibilité comme relation d'ordre. Cet ensemble partiellement ordonné est toujours un treillis distributif. C'est une algèbre booléenne si et seulement si n est sans facteur carré.

Soit l'entier naturel donné n, définissons le radical de l'entier n par

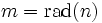$m = \operatorname{rad}(n)\,$ ,

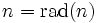égal au produit des nombres premiers p divisant n. Alors, les nombres sans facteur carré n sont exactement les solutions de $n = \operatorname{rad}(n)\,$ .

Distribution des nombres sans facteur carré

Si 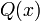$Q(x)\,$ représente le nombre d'entiers sans facteur carré entre 1 et x, alors

$Q(x) = \frac{6x}{\pi^2} + O(\sqrt{x})$

(voir pi et notation grand O). La densité naturelle asymptotique des nombres sans facteur carré est par conséquent

$\lim_{x\to\infty} \frac{Q(x)}{x} = \frac{6}{\pi^2} = \frac{1}{\zeta(2)}$

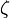où $\zeta\,$ est la fonction Zeta de Riemann.

De même, si 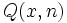$Q(x,n)\,$ représente le nombre d'entiers sans n-ième puissance entre 1 et x, on peut montrer

$\lim_{x\to\infty} \frac{Q(x,n)}{x} = \frac{1}{\zeta(n)}.$

Ensembles d'entiers sur la base de leur divisibilité
Formes de factorisation :	Nombre premier · Nombre composé · Nombre puissant · Entier sans facteur carré
Sommes de diviseurs :	Nombre parfait · Nombre presque parfait · Nombre quasi parfait · Nombre parfait multiple · Nombre hyperparfait · Nombre parfait unitaire · Nombre semi-parfait · Nombre semi-parfait primitif · Nombre pratique
Nombres de diviseurs :	Nombre abondant · Nombre hautement abondant · Nombre superabondant · Nombre colossalement abondant · Nombre hautement composé
Autres :	Nombre déficient · Nombre étrange · Nombre amical · Nombre sociable · Nombre solitaire · Nombre sublime · Nombre à moyenne harmonique entière · Nombre frugal · Nombre équidigital · Nombre extravagant

Portail des mathématiques

Ce document provient de « Entier sans facteur carr%C3%A9 ».

Catégories : Divisibilité et factorisation | Propriété arithmétique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Entier Sans Facteur Carré de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

Entier sans facteur carre — Entier sans facteur carré En mathématiques et plus précisément en arithmétique modulaire, un entier sans facteur carré est un entier divisible par aucun carré parfait, excepté 1. Par exemple, 10 est sans facteur carré mais 18 ne l est pas, comme… … Wikipédia en Français
Entier sans facteur carré — En mathématiques et plus précisément en arithmétique modulaire, un entier sans facteur carré est un entier divisible par aucun carré parfait, excepté 1. Par exemple, 10 est sans facteur carré mais 18 ne l est pas, comme il est divisible par . Les … Wikipédia en Français
Sans carré — Entier sans facteur carré En mathématiques et plus précisément en arithmétique modulaire, un entier sans facteur carré est un entier divisible par aucun carré parfait, excepté 1. Par exemple, 10 est sans facteur carré mais 18 ne l est pas, comme… … Wikipédia en Français
Entier (nombre) — Entier naturel Pour les articles homonymes, voir Entier (homonymie). Les entiers naturels permettent de compter (une pomme, deux pommes, trois pommes...). Un entier natur … Wikipédia en Français
Entier Naturel — Pour les articles homonymes, voir Entier (homonymie). Les entiers naturels permettent de compter (une pomme, deux pommes, trois pommes...). Un entier natur … Wikipédia en Français
Entier positif — Entier naturel Pour les articles homonymes, voir Entier (homonymie). Les entiers naturels permettent de compter (une pomme, deux pommes, trois pommes...). Un entier natur … Wikipédia en Français
Entier quadratique — Pour les articles homonymes, voir Entier (homonymie). En mathématiques, un entier quadratique est un nombre réel ou complexe, racine d un polynôme du second degré à coefficients dans les nombres entiers et dont le coefficient du terme du plus… … Wikipédia en Français
Entier naturel — Pour les articles homonymes, voir Entier (homonymie). En mathématiques, un entier naturel est un nombre positif ou nul permettant fondamentalement de dénombrer des objets comptant chacun pour un. Un tel nombre entier peut s écrire avec une suite… … Wikipédia en Français
Entier Algébrique — Pour les articles homonymes, voir Entier (homonymie). En mathématiques, les entiers algébriques forment une famille de nombres qui généralise l ensemble des nombres entiers dits relatifs. Ils jouent un rôle analogue à ces derniers en théorie… … Wikipédia en Français
Entier algebrique — Entier algébrique Pour les articles homonymes, voir Entier (homonymie). En mathématiques, les entiers algébriques forment une famille de nombres qui généralise l ensemble des nombres entiers dits relatifs. Ils jouent un rôle analogue à ces… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Entier Sans Facteur Carré