Ensemble Infini

Ensemble Infini

Ensemble infini

L'infini se définit par rapport au fini, mais le terme "fini" peut avoir plusieurs sens selon le contexte ; ainsi un segment de droite, limité en longueur, a un nombre infini de points.

Du point de vue de la théorie des ensembles, le fini se définit par un nombre d'éléments ; mais cela même demande à être clarifié, d'autant plus que ce concept de finitude peut varier selon la théorie dans laquelle on se place.

Un ensemble E est fini s'il existe une bijection de E sur un intervalle [1,n] formé par les nombres entiers naturels de 1 à n inclus, ou de façon équivalente sur l'intervalle [0,n-1] des n premiers entiers naturels.[1]

Il existe des définitions basées sur les propriétés intrinsèques des ensembles finis :[2]

  • Selon Dedekind, un ensemble E est fini exactement s'il n'existe aucun sous-ensemble propre B de E tel qu'on puisse définir une relation biunivoque entre E et B.
  • Selon Tarski, un ensemble E est fini exactement si toute famille non vide B de sous-ensembles de E admet un élément Bo minimal pour l'inclusion.

Ces deux définitions ne sont équivalentes que grâce à l'axiome du choix ; sans cet axiome, la définition de Tarski est la plus forte, et correspond à la définition donnée au début.

Si 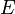\quad E est un ensemble infini alors 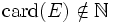\mathrm{card}(E) \notin \mathbb{N}  : le cardinal de E n'est pas un entier naturel ; toutefois ceci présuppose que tout ensemble a un cardinal ; or cette affirmation repose sur l'axiome du choix.[3]

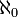La classe la plus simple des ensembles infinis est la classe des ensembles infinis dits dénombrables (équipotents à \mathbb{N}). Une autre classe d'ensembles infinis est la classe des ensembles équipotents à \mathbb R qui sont parfois appelés ensembles continus. 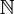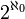Se pose alors le problème de l'hypothèse du continu : existe-t-il un ensemble dont le cardinal est strictement compris entre \aleph_0, qui est le cardinal de \mathbb N et 2^{\aleph_0} qui est le cardinal de \mathbb{R} ? Cette proposition est indécidable dans le système d'axiomes ZFC.

Article détaillé : Nombre cardinal.

Notes et références

  1. ↑ Selon une terminologie largement acceptée, un entier est un ordinal α tel que tout β, Ø<β≤α a un prédécesseur ; alors l'intervalle [0,n-1] s'identifie à n lui-même, de sorte qu'un ensemble est fini exactement s'il est équipotent "à un entier".
  2. ↑ Roland Fraïssé, Logique mathématique, Vol.I, Gauthier-Villars Paris 1971, pp.12-13-14
  3. ↑ Jean-Louis Krivine, Théorie axiomatique des ensembles, P.U.F. Paris 1972 p. 38
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Ensemble infini ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Ensemble Infini de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Ensemble infini — ● Ensemble infini ensemble qui peut être mis en bijection avec l une de ses parties propres …   Encyclopédie Universelle

  • Ensemble infini — En mathématiques, plus précisément en théorie des ensembles, un ensemble infini est un ensemble qui n est pas fini, c est à dire qu il n y a aucun moyen de « compter » les éléments de cet ensemble à l aide d un ensemble borné d entiers …   Wikipédia en Français

  • Ensemble infini non dénombrable — Cet article court présente un sujet plus développé dans : Ensemble dénombrable et Ensemble infini. Un ensemble infini non dénombrable est un ensemble qui est « trop gros » pour être dénombrable. De manière précise, c est un… …   Wikipédia en Français

  • Ensemble Dénombrable — En mathématiques, un ensemble est dit dénombrable, ou infini dénombrable, lorsque ses éléments peuvent être listés sans omission ni répétition dans une suite indexée par les entiers. Certains ensembles infinis, au contraire, contiennent trop d… …   Wikipédia en Français

  • Ensemble denombrable — Ensemble dénombrable En mathématiques, un ensemble est dit dénombrable, ou infini dénombrable, lorsque ses éléments peuvent être listés sans omission ni répétition dans une suite indexée par les entiers. Certains ensembles infinis, au contraire,… …   Wikipédia en Français

  • INFINI MATHÉMATIQUE — Le mot «infini» désigne un concept à entrées multiples. Il s’ouvre d’abord sur l’ontologie et signifie alors, selon la tradition, «l’être tel qu’on n’en saurait concevoir de plus grand» («ens quo majus concipi non potest »). Ce fut pour une… …   Encyclopédie Universelle

  • INFINI — La philosophie a emprunté la notion de l’infini – corrélative de la notion du fini – à la réflexion sur l’exercice de la connaissance, d’une part; à l’expérience ou à la tradition religieuse, de l’autre. Ces deux sources déterminent la variété… …   Encyclopédie Universelle

  • Ensemble Fini — En mathématiques, un ensemble E est dit fini si et seulement s il existe un entier n et une bijection de E sur l ensemble des entiers naturels strictement plus petits que n, en particulier, si n = 0, E est l ensemble vide qui est donc bien fini.… …   Wikipédia en Français

  • Ensemble Indénombrable — Ensemble infini non dénombrable Cet article court présente un sujet plus amplement développé ici : Ensemble dénombrable et Ensemble infini. Un ensemble infini non dénombrable est un ensemble qui est « trop gros » pour être… …   Wikipédia en Français

  • Ensemble indenombrable — Ensemble infini non dénombrable Cet article court présente un sujet plus amplement développé ici : Ensemble dénombrable et Ensemble infini. Un ensemble infini non dénombrable est un ensemble qui est « trop gros » pour être… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”