Loi géométrique

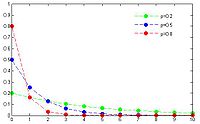
Géometrique
Densité de probabilité / Fonction de masse
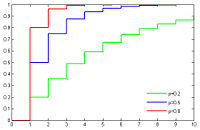
Fonction de répartition

Paramètres	$0< p \leq 1$ probabilité de succès (réel), $q = 1 - p$ probabilité d'échec
Support	$k \in \{1,2,3,\dots\}\!$
Densité de probabilité (fonction de masse)	$q^{k-1}\,p\!$
Fonction de répartition	$1-q^k\!$
Espérance	$\frac{1}{p}\!$
Médiane (centre)	$\left\lceil \frac{-\log(2)}{\log(q)} \right\rceil\!$ (pas unique si $- log(2) / log(q)$ est entier)
Mode	1
Variance	$\frac{q}{p^2}\!$
Asymétrie	$\frac{2-p}{\sqrt{q}}\!$
Kurtosis normalisé	$6+\frac{p^2}{q}\!$
Entropie	$\frac{-q\log_2 q - p \log_2 p}{p}\!$
Fonction génératrice des moments	$\frac{pe^t}{1-(1-p) e^t}\!$
Fonction caractéristique	$\frac{pe^{it}}{1-q\,e^{it}}\!$
modifier

La loi géométrique est une loi de probabilité apparaissant dans de nombreuses applications. La loi géométrique de paramètre p (0 < p < 1) correspond au modèle suivant :

On considère une épreuve de Bernoulli dont la probabilité de succès est p et celle d'échec q = 1 - p.

On renouvelle cette épreuve de manière indépendante jusqu'au premier succès. On appelle X la variable aléatoire donnant le rang du premier succès.

Les valeurs de X sont les entiers naturels non nuls 1, 2, 3, ... La probabilité que X = k est alors, pour k = 1, 2, 3, ...

p (k) = q k - 1 p .

On dit que X suit une loi géométrique de paramètre p.

Sommaire

1 Calcul de p(k)
2 Définition alternative
3 Date de mort, durée de vie
4 Espérance, variance, écart type
5 Liens avec d'autres lois
- 5.1 Lien avec la loi exponentielle
- 5.2 Lien avec la loi binomiale négative
6 Voir aussi

Calcul de p(k)

La probabilité p(k) correspond à la probabilité d'obtenir dans une succession de k épreuves de Bernoulli, k − 1 échecs suivis d'un succès. Les épreuves étant indépendantes, cette probabilité est de q^{k − 1}p.

Définition alternative

On rencontre parfois pour la loi géométrique, la définition alternative suivante : la probabilité p'(k) est la probabilité, lors d'une succession d'épreuves de Bernoulli indépendantes, d'obtenir k échecs suivi d'un succès. Elle modélise la durée de vie d'une entité qui aurait, à tout instant la probabilité p de mourir. On obtient alors, pour k = 0, 1, 2, ...

p'(k) = q k p .

On remarque qu'il ne s'agit que d'un décalage de la précédente loi géométrique. Son espérance n'est plus alors de $\scriptstyle \frac 1p$ mais de $\scriptstyle \frac 1p - 1$ , c'est-à-dire $\scriptstyle \frac qp$ . La variance est identique pour les deux définitions. Dans la suite, on prendra la première définition.

Date de mort, durée de vie

Si on appelle p la probabilité de désintégration d'une particule radioactive, la loi géométrique est le premier modèle discret de la mort d'une particule radioactive. La durée de vie de la particule radioactive V, suit la loi de probabilité suivante :

P (V = k) = q k p

pour k = 0, 1, ....

$P(V \geq k) =q^k = \mathrm{e}^{k\ln(q)}$

Pour p petit, ln(1 - p) est voisin de -p donc

$P(V \geq k) \approx \mathrm{e}^{-pk}$

où l'on retrouve la distribution de la loi exponentielle.

Espérance, variance, écart type

L'espérance d'une variable aléatoire suivant une loi géométrique de paramètre p est $\frac{1}{p}$

La variance est $\frac{q}{p^2}$ ,

L'écart type est donc $\frac{\sqrt{q}}{p}$

Démonstration

Calculs préliminaires, pour tout x de [0 ; 1[,

$\begin{align} f(x)&= \sum_{k=1}^{+\infty} x^{k-1} = \sum_{k=0}^{+\infty} x^{k} = \frac{1}{1-x}\\ f^{\prime}(x)&= \sum_{k=1}^{+\infty} kx^{k-1} = \sum_{k=0}^{+\infty} (k+1)x^{k} = \frac{1}{(1-x)^2}\\ f^{\prime\prime}(x)&= \sum_{k=1}^{+\infty} k(k+1)x^{k-1}= \sum_{k=1}^{+\infty}k^2x^{k-1} + \sum_{k=1}^{+\infty} kx^{k-1}= \frac{2}{(1-x)^3} \end{align}$

En particulier

$\sum_{k=1}^{+\infty}k^2x^{k-1} = \frac{2}{(1-x)^3} - \frac{1}{(1-x)^2}$

On peut alors utiliser ces identités pour le calcul de l'espérance :

$\begin{align}\mathbb{E}[X] &= \sum_{k=1}^{+\infty} kq^{k-1} p\\ &= \frac{p}{(1-q)^2}\\&= \frac 1p,\end{align}$

car $1 - q = p,$ et pour celui de la variance :

$\begin{align} V(X)&= \left(\sum_{k=1}^{+\infty} k^2q^{k-1} p\right) - \mathbb{E}[X]^2\\&= \frac{2p}{(1-q)^3}- \frac{p}{(1-q)^2} - \frac{1}{p^2}\\&= \frac{2}{p^2} - \frac 1p-\frac{1}{p^2}\\&= \frac{q}{p^2}.\end{align}$

Liens avec d'autres lois

Lien avec la loi exponentielle

La loi géométrique est une version discrétisée de la loi exponentielle. En conséquence, la loi exponentielle est une limite de lois géométriques renormalisées.

Propriété — Si $\scriptstyle\ X\$ suit la loi exponentielle d'espérance 1, et si $\scriptstyle\ Y=\lceil\theta X\rceil,\ \theta>0,\$ alors $\scriptstyle\ Y\$ suit la loi géométrique de paramètre

$p\ =\ 1-e^{-\ \tfrac{1}{\theta}}.$

Démonstration

$\begin{align} \mathbb{P}(Y=k) &= \mathbb{P}(\lceil\theta X\rceil=k) \\ &= \mathbb{P}(\theta X\in]k-1,k]) \\ &= \mathbb{P}\left(X\in\left]\tfrac{k-1}{\theta},\tfrac{k}{\theta}\right]\right) \\ &= F_X\left(\tfrac{k}{\theta}\right)-F_X\left(\tfrac{k-1}{\theta}\right) \\ &= \exp\left(-\ \tfrac{k-1}{\theta}\right)-\exp\left(-\ \tfrac{k}{\theta}\right) \\ &= \left(e^{-\ \tfrac{1}{\theta}}\right)^{k-1}\ \left(1-e^{-\ \tfrac{1}{\theta}}\right). \end{align}$

Diagramme en bâtons de la loi de V et densité de la loi exponentielle de paramètre 1/10.

Notons que, pour un nombre réel $\scriptstyle\ x,\$ $\scriptstyle\ \lceil x\rceil\$ désigne la partie entière supérieure de $\scriptstyle\ x,\$ définie par

$\lceil x\rceil\ =\ \min\left\{k\in\mathbb{Z}\ |\ k\ge x\right\}.$

Conséquence :

Ainsi, pour obtenir une variable aléatoire $\scriptstyle\ Y^{\prime}\$ suivant une loi géométrique de paramètre $\scriptstyle\ p\$ arbitraire (avec toutefois la contrainte $\scriptstyle\ 0<p<1\$ ), à partir d'une variable aléatoire exponentielle $\scriptstyle\ X^{\prime}\$ de paramètre $\scriptstyle\ \lambda,\$ il suffit de poser

$Y^{\prime}=\lceil\theta X^{\prime}\rceil,$

où l'on a choisi

$\theta\ =\ -\tfrac{\lambda}{\ln\left(1-p\right)}.$

En effet, $\scriptstyle\ X=\lambda\,X^{\prime}\$ suit une loi exponentielle de paramètre 1 (et d'espérance 1).

Réciproquement,

Propriété — Si, pour $\scriptstyle\ n\ge 1,\$ la variable aléatoire $\scriptstyle\ Y_n\$ suit la loi géométrique de paramètre $\scriptstyle\ p_n\$ , et si, simultanément,

$\lim_n p_n\ =\ 0\qquad\text{et}\qquad\lim_n p_n/a_n\ =\ \lambda>0,$

alors $\scriptstyle\ a_nY_n\$ converge en loi vers la loi exponentielle de paramètre $\scriptstyle\ \lambda.\$

Démonstration

On se donne une variable aléatoire exponentielle $\scriptstyle\ X\$ de paramètre 1, et on pose

$\begin{align} \theta_n &= -\tfrac{1}{\ln\left(1-p_n\right)}, \\ Y^{\prime}_n &= \lceil\theta_n X\rceil. \end{align}$

Alors $\scriptstyle\ Y_n\$ et $\scriptstyle\ Y^{\prime}_n\$ ont même loi, en vertu de la propriété précédente. Par ailleurs, pour tout $\scriptstyle\ \omega,\$

$\lim_n a_nY^{\prime}_n(\omega)\ =\ \lim_n a_n\lceil\theta_n X(\omega)\rceil=\ \left(\lim_n a_n\theta_n\right)\ X(\omega)\ =\ X(\omega)/\lambda.$

Or d'une part la convergence presque sûre entraine la convergence en loi, d'autre part la loi de $\scriptstyle\ X/\lambda\$ est la loi exponentielle de paramètre $\scriptstyle\ \lambda.\$

Lien avec la loi binomiale négative

Si X_n est une variable aléatoire distribuée selon la loi binomiale négative de paramètres n et p, alors X_n a même loi que la somme de n variables aléatoires indépendantes distribuées selon une loi géométrique de paramètre p.

Voir aussi

v · Lois de probabilités

Lois discrètes

à support fini	Loi de Bernoulli • Loi uniforme discrète • Loi binomiale • Loi hypergéométrique • Loi de Benford
à support dénombrable	Loi géométrique • Loi de Poisson • Loi binomiale négative • Loi logarithmique

Lois continues

à support compact	Loi uniforme continue • Loi triangulaire • Loi bêta
à support semi-infini	Loi exponentielle • Loi Gamma • Loi du χ² • Loi de Fisher • Loi de Weibull • Loi de Rayleigh • Loi de Rice • Loi d'Erlang • Loi de Lévy • Loi inverse-gamma • Loi log-normale
à support infini	Loi normale • Loi normale asymétrique • Loi de Cauchy • Loi de Laplace • Loi logistique • Loi de Student • Loi stable • Loi de Gumbel

v · Probabilités et statistiques

Théorie des probabilités

Axiomes des probabilités • Espace probabilisable • Probabilité • Événement • Tribu • Indépendance

Probabilités élémentaires	Moyenne • Espérance • Médiane • Variance • Écart type
Loi de probabilité	Variable aléatoire • Loi de Bernoulli • Loi de Poisson • Loi uniforme • Loi normale • Loi de Student • Loi de Fisher • Variables iid
Convergence de lois	Théorème central limite • Loi des grands nombres • Théorème de Borel-Cantelli
Calcul stochastique	Marche aléatoire • Chaîne de Markov • Processus stochastique • Processus de Markov • Martingale • Mouvement brownien • Équation différentielle stochastique

Statistiques

Statistique descriptive	Échantillon • Quantile • Intervalle de confiance • Représentations de données • Histogramme • Diagramme circulaire • Boîte à moustaches • Régression linéaire • Méthode des moindres carrés
Statistique mathématique	Fonction de répartition empirique • Théorème de Glivenko-Cantelli • Inférence bayésienne
Tests statistiques	Test d'hypothèse • Hypothèse statistique • Estimateur • Test du χ² • Test t • Test de Fisher

Applications

Économétrie • Mécanique statistique • Jeu de hasard • Biomathématique • Mathématiques financières

Portail des probabilités et des statistiques

Catégories :

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Loi géométrique de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Loi Géométrique — Geometrique Densité de probabilité / Fonction de masse Fonction de répartition … Wikipédia en Français
Loi geometrique — Loi géométrique Geometrique Densité de probabilité / Fonction de masse Fonction de répartition … Wikipédia en Français
Loi géométrique — ● Loi géométrique loi de probabilité d une variable aléatoire discrète X prenant ses valeurs dans N et dont la fonction de distribution est P(X = k) = pqk, où 0 < p < 1 et q = 1 − p … Encyclopédie Universelle
Loi de Pascal — Loi géométrique Geometrique Densité de probabilité / Fonction de masse Fonction de répartition … Wikipédia en Français
Loi Exponentielle — Exponentielle Densité de probabilité / Fonction de masse Fonction de répartition … Wikipédia en Français
Loi De Probabilité — Une loi de probabilité ou distribution de probabilité a commencé par décrire les répartitions typiques des fréquences d apparition des résultats d un phénomène aléatoire. Dans le dernier quart du XXe siècle, on a largement étendu le concept… … Wikipédia en Français
Loi de probabilite — Loi de probabilité Une loi de probabilité ou distribution de probabilité a commencé par décrire les répartitions typiques des fréquences d apparition des résultats d un phénomène aléatoire. Dans le dernier quart du XXe siècle, on a largement … Wikipédia en Français
Loi log-normale — Densité de probabilité / Fonction de masse μ=0 Fonction de répartition μ=0 … Wikipédia en Français
Loi logistique — Densité de probabilité / Fonction de masse Fonction de répartition … Wikipédia en Français
Loi uniforme discrète — Densité de probabilité / Fonction de masse n=5 où n = b − a + 1 Fonction de répartition … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Loi géométrique

Sommaire

Calcul de p(k)

Définition alternative

Date de mort, durée de vie

Espérance, variance, écart type