Loi bêta

Loi bêta
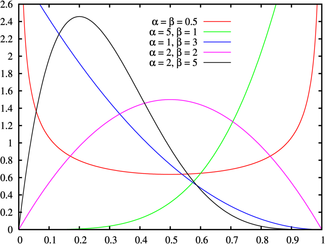
Beta
Densité de probabilité / Fonction de masse
Probability density function for the Beta distribution
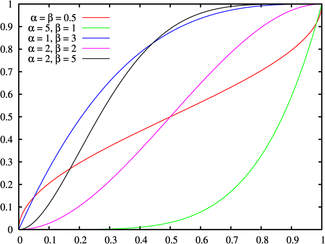
Fonction de répartition
Cumulative distribution function for the Beta distribution
Paramètres α > 0 forme (réel)
β > 0 forme (réel)
Support x \in [0; 1]\!
Densité de probabilité (fonction de masse) \frac{x^{\alpha-1}(1-x)^{\beta-1}} {\mathrm{B}(\alpha,\beta)}\!
Fonction de répartition I_x(\alpha,\beta)\!
Espérance \frac{\alpha}{\alpha+\beta}\!
Mode \frac{\alpha-1}{\alpha+\beta-2}\! pour α > 1,β > 1
Variance \frac{\alpha\beta}{(\alpha+\beta)^2(\alpha+\beta+1)}\!
Asymétrie \frac{2\,(\beta-\alpha)\sqrt{\alpha+\beta+1}}{(\alpha+\beta+2)\sqrt{\alpha\beta}}
Kurtosis normalisé 6\,\tfrac{\alpha^3-\alpha^2(2\beta-1)+\beta^2(\beta+1)-2\alpha\beta(\beta+2)}{\alpha \beta (\alpha+\beta+2) (\alpha+\beta+3)}\!
Fonction génératrice des moments 1 +\sum_{k=1}^{\infty} \left( \prod_{r=0}^{k-1} \frac{\alpha+r}{\alpha+\beta+r} \right) \frac{t^k}{k!}
Fonction caractéristique {}_1F_1(\alpha; \alpha+\beta; i\,t)\!
modifier Consultez la documentation du modèle

Dans la théorie des probabilités et en statistiques, la loi bêta est une famille de lois de probabilités continues, définies sur [0,1], paramétrée par deux paramètres de forme, typiquement notés α et β. C'est un cas spécial de la loi de Dirichlet, avec seulement deux paramètres.

Sommaire

Caractérisation

Fonction de densité

La densité de probabilité de la loi bêta est:

f(x;\alpha,\beta) = \frac{x^{\alpha-1}(1-x)^{\beta-1}}{\int_0^1 u^{\alpha-1} (1-u)^{\beta-1}\, du} \!
= \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}\, x^{\alpha-1}(1-x)^{\beta-1}\!
= \frac{1}{\mathrm{B}(\alpha,\beta)}\, x ^{\alpha-1}(1-x)^{\beta-1}\!

où Γ est la fonction gamma. La fonction bêta, B, apparaît comme une constante de normalisation, permettant à la densité de s'intégrer à l'unité.

Fonction de répartition

La fonction de répartition est

F(x;\alpha,\beta) = \frac{\mathrm{B}_x(\alpha,\beta)}{\mathrm{B}(\alpha,\beta)} = I_x(\alpha,\beta) \!

où Bx(α,β) est la fonction bêta incomplète et Ix(α,β) est la fonction bêta incomplète régularisée.

Propriétés

Moments

L'espérance et la variance d'une variable aléatoire bêta de paramètres α et β sont donnés par la formule:

\begin{align} \operatorname{E}(X) = & \frac{\alpha}{\alpha+\beta} \\ \operatorname{Var}(X) = & \frac{\alpha \beta}{(\alpha+\beta)^2(\alpha+\beta+1)} \end{align}

L'asymétrie est

\frac{2 (\beta - \alpha) \sqrt{\alpha + \beta + 1} }{(\alpha + \beta + 2) \sqrt{\alpha \beta}}\!.

Le kurtosis normalisé (excès d'aplatissement) est:

6\,\frac{\alpha^3-\alpha^2(2\beta-1)+\beta^2(\beta+1)-2\alpha\beta(\beta+2)}{\alpha \beta (\alpha+\beta+2) (\alpha+\beta+3)}\!.

Formes

La densité de la loi bêta peut prendre différentes formes selon les valeurs des deux paramètres:

  • \alpha < 1,\ \beta < 1 est en forme de U (graphe rouge);
  • \alpha < 1,\ \beta \geq 1 ou \alpha = 1,\ \beta > 1 est strictement décroissant (graphe bleu);
  • \alpha = 1,\ \beta = 1 est la loi uniforme continue;
  • \alpha = 1,\ \beta < 1 ou \alpha > 1,\ \beta \leq 1 est strictement croissant (graphe vert);
    • \alpha > 2,\ \beta = 1 est strictement convexe;
    • \alpha = 2,\ \beta = 1 est une droite;
    • 1 < \alpha < 2,\ \beta = 1 est strictement concave;
  • \alpha > 1,\ \beta > 1 est unimodal (graphes noir et violet).

Qui plus est, si α = β alors la densité est symétrique autour de 1/2 (graphes rouge et violet).

Estimation des paramètres

Soit la moyenne empirique

\bar{x} = \frac{1}{N}\sum_{i=1}^N x_i

et

v = \frac{1}{N}\sum_{i=1}^N (x_i - \bar{x})^2

la variance. La méthode des moments fournit les estimations suivantes:

\alpha = \bar{x} \left(\frac{\bar{x} (1 - \bar{x})}{v} - 1 \right),
\beta = (1-\bar{x}) \left(\frac{\bar{x} (1 - \bar{x})}{v} - 1 \right).


Distributions associées

  • Si X a une distribution bêta, alors la variable aléatoire T = \frac{X}{1-X} est distribuée selon la distribution bêta du second type ;
  • La loi Beta(1,1) est identique à la Loi uniforme continue ;
  • Si X et Y sont indépendamment distribués selon une loi Gamma, de paramètres (α,θ) et (β,θ) respectivement, alors la variable aléatoire \frac{X}{X+Y} est distribuée selon une loi Beta(α,β) ;
  • Si X \sim {\rm U}(0; 1)\, selon une loi uniforme, alors X^2 \sim {\rm Beta}(1/2,1) \  ;
  • La k-ème statistique d'ordre d'un n-échantillon de lois uniformes \ {\rm U}(0, 1]\, suit la loi {\rm Beta}(k,n-k+1) \ .

Liens externes

v · Lois de probabilités
Lois discrètes
à support fini Loi de Bernoulli • Loi uniforme discrète • Loi binomiale • Loi hypergéométrique • Loi de Benford
à support dénombrable Loi géométrique • Loi de Poisson • Loi binomiale négative • Loi logarithmique
Lois continues
à support compact Loi uniforme continue • Loi triangulaire • Loi bêta
à support semi-infini Loi exponentielle • Loi Gamma • Loi du χ² • Loi de Fisher • Loi de Weibull • Loi de Rayleigh • Loi de Rice • Loi d'Erlang • Loi de Lévy • Loi inverse-gamma • Loi log-normale
à support infini Loi normale • Loi normale asymétrique • Loi de Cauchy • Loi de Laplace • Loi logistique • Loi de Student • Loi stable • Loi de Gumbel
  • Portail des probabilités et des statistiques Portail des probabilités et des statistiques

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Loi bêta de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Loi Uniforme Continue — Uniforme Densité de probabilité / Fonction de masse Fonction de répartition …   Wikipédia en Français

  • Loi de Fisher-Snedecor — Loi de Fisher Fisher Snedecor Densité de probabilité / Fonction de masse Fonction de répartition …   Wikipédia en Français

  • Loi logistique — Densité de probabilité / Fonction de masse Fonction de répartition …   Wikipédia en Français

  • Loi log-normale — Densité de probabilité / Fonction de masse μ=0 Fonction de répartition μ=0 …   Wikipédia en Français

  • Loi uniforme discrète — Densité de probabilité / Fonction de masse n=5 où n = b − a + 1 Fonction de répartition …   Wikipédia en Français

  • Loi inverse-gamma — Inverse gamma Densité de probabilité / Fonction de masse Fonction de répartition …   Wikipédia en Français

  • Loi uniforme continue — Uniforme Densité de probabilité / Fonction de masse Fonction de répartition …   Wikipédia en Français

  • Loi de Fisher — Fisher Snedecor Densité de probabilité / Fonction de masse Fonction de répartition …   Wikipédia en Français

  • Loi normale — Distribution gaussienne Densité de probabilité / Fonction de masse La courbe rouge représente la fonction φ (voir texte), densité de probabilité d une variable suivant une loi normale centrée réduite Fonction de répartition …   Wikipédia en Français

  • Loi de Dirichlet — Plusieurs images de la densité de la loi de Dirichlet distribution lorsque K=3 pour différents vecteurs de paramètres α. Dans le sens horaire à partir du coin supérieur gauche : α=(6, 2, 2), (3, 7, 5), (6, 2, 6) …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”