Loi Hypergéométrique

Loi hypergéométrique

**Hypergéométrique**
Densité de probabilité / Fonction de masse
Fonction de répartition
Paramètres	$\begin{align}A&\in 0,1,2,\dots \\ p&\in [0;1] \\ n&\in 0,1,2,\dots,N\end{align}\,$
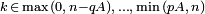
Support	$\scriptstyle{k\, \in\, \max{(0,\, n-qA)},\, \dots,\, \min{(pA,\, n )}}\,$
Densité de probabilité (fonction de masse)	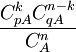$\frac{C_{pA}^kC_{qA}^{n-k}}{C_A^n}$
Fonction de répartition
Espérance	$n p$
Médiane (centre)
Mode	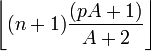$\left \lfloor (n+1)\frac{(pA+1)}{A+2} \right \rfloor$
Variance	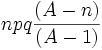$npq\frac{(A-n)}{(A-1)}$
Asymétrie (statistique)	$\frac{(A-2n)(1-2p)(A-1)^\frac{1}{2}}{[npq(A-n)]^\frac{1}{2}(A-2)}$
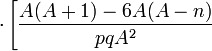
Kurtosis (non-normalisé)	$\left[\frac{A^2(A-1)}{n(A-2)(A-3)(A-n)}\right]$ $\cdot\left[\frac{A(A+1)-6A(A-n)}{pqA^2}\right.$ $+\left.\frac{3n(A-n)(A+6)}{A^2}-6\right]$
Entropie
Fonction génératrice des moments	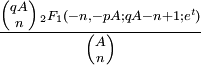$\frac{{qA \choose n} \scriptstyle{\,_2F_1(-n, -pA; qA - n + 1; e^{t}) } } {{A \choose n}} \,\!$
Fonction caractéristique	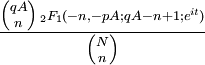$\frac{{qA \choose n} \scriptstyle{\,_2F_1(-n, -pA; qA - n + 1; e^{it}) }} {{N \choose n}}$

Une loi hypergéométrique de paramètres n, p et A correspond au modèle suivant:

On tire simultanément n boules dans une urne contenant pA boules gagnantes et qA boules perdantes (avec q = 1 - p). On compte alors le nombre de boules gagnantes extraites et on appelle X la variable aléatoire donnant le nombre de boules gagnantes.

L'univers X(Ω) est l'ensemble des entiers de 0 à n. La variable aléatoire suit une loi de probabilité définie par

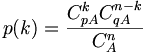$p(k)=\frac{C_{pA}^kC_{qA}^{n-k}}{C_A^n}$ .

Cette loi de probabilité s'appelle la loi hypergéométrique de paramètres (n ; p ; A). Il est nécessaire que p soit un réel compris entre 0 et 1, que pA soit entier et que n ≤ A. Lorsque ces conditions ne sont pas imposées, l'ensemble des possibles X(Ω) est l'ensemble des entiers entre max(0;n-qA) et min(pA;n).

Une autre paramétrisation très répandue consiste à considérer une loi Hypergéométrique de paramètres (A, N_a, n) avec A le nombre total de boules, N_a le nombre de boules à succès (ici pA) et n le nombre de tirages.

Calcul de p(k)

Il s'agit d'un tirage simultané (c'est-à-dire non ordonné et sans remise) de n éléments parmi A. Tirage que l'on considère comme équiprobable.

La combinatoire permet de dire que le cardinal de l'univers est $C_A^n$ .

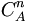	Tirage	Resté dans l'urne	Total
succès	k	pA-k	pA
échec	n-k	qA - n + k	qA
Total	n	A-n	A

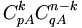L'événement « X=k » (voir tableau) signifie que l'on a tiré k boules gagnantes parmi pA et n - k boules perdantes parmi qA. Le cardinal de cet événement est donc $C_{pA}^kC_{qA}^{n-k}$ .

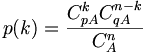
La probabilité de l'événement est donc $p(k)=\frac{C_{pA}^kC_{qA}^{n-k}}{C_A^n}$

Espérance, variance et écart type

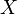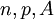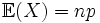L'espérance d'une variable aléatoire suivant une loi hypergéométrique est la même que dans le cas binômiale. $X\,$ suit une loi hypergéométrique de paramètres $n, p, A\,$ , alors son espérance est $\mathbb{E}(X)=np\,$ .

Démonstration

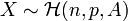
On se donne: $X \sim \mathcal{H}(n,p,A)$

(si on se rapporte à un modèle d'urnes à tirage simultané, c'est-à-dire non ordonné et sans remise. On a donc 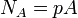$N_A = pA\,$ : le nombre de boules de type "réussite" et 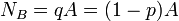$N_B = qA = (1-p)A\,$ : le nombre de boules de type "échec".)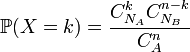

$\mathbb{P}(X=k)=\frac{C_{N_A}^kC_{N_B}^{n-k}}{C_A^n}$

Numérotons de 1 à 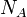$N_A\,$ les boules de type "réussite" et définissons pour tout 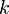$k\,$ compris entre 1 et 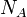$N_A\,$ l'événement:

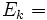$E_k=\,$ { on a tiré parmi les n boules la boule de type "réussite" k }. Comme le nombre total 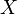$X\,$ de boules de type "réussite" tirées est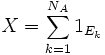 $X=\sum_{k=1}^{N_A}1_{E_k}\,$

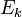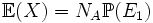(où 1 est la Fonction indicatrice de $E_k\,$ ), par linéarité de l'espérance, $\mathbb{E}(X)=N_A\mathbb{P}(E_1)\,$ .

Évaluons maintenant 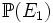$\mathbb{P}(E_1)\,$ . En passant au complémentaire,

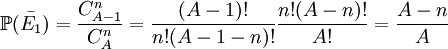$\mathbb{P}\bar{(E_1)}=\frac{C_{A-1}^n}{C_A^n}=\frac{(A-1)!}{n!(A-1-n)!} \frac{n!(A-n)!}{A!}=\frac{A-n}{A}\,$ qui est la probabilité de ne jamais tirer une boule donnée.

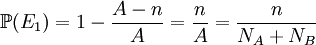
Donc $\mathbb{P}(E_1)=1-\frac{A-n}{A}=\frac{n}{A}=\frac{n}{N_A+N_B}\,$

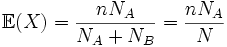
On en conclut donc que $\mathbb{E}(X)=\frac{nN_A}{N_A+N_B}=\frac{nN_A}{N}\,$

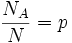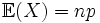En rappelant que $\frac{N_A}{N}=p\,$ qui est exactement la probabilité d'avoir un succès, on a bien $\mathbb{E}(X)=np\,$ .

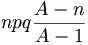
La variance d'une variable aléatoire suivant une loi hypergéométrique de paramètres n, p, A est $npq\frac{A - n}{A - 1}$

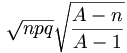L'écart type est alors $\sqrt{npq}\sqrt{\frac{A - n}{A - 1}}$ .

Convergence

Pour n petit devant A, la loi hypergéométrique est équivalente à une loi binomiale de paramètres n et p. En fait, on considère que, pour A grand, tirer simultanément n boules revient à effectuer n fois une épreuve de Bernoulli dont la probabilité de succès serait p (p est la proportion de boules gagnantes dans l'ensemble des boules), car il est très peu probable de retomber sur la même boule, même si on la replace dans l'urne.

En pratique, on remplace la loi hypergéométrique de paramètres (n ; p ; A) par une loi binomiale de paramètres (n ; p) dès que 10n < A.

Un exemple très classique de ce remplacement concerne le sondage. On considère fréquemment le sondage de n personnes comme n sondages indépendants alors qu'en réalité le sondage est exhaustif (on n'interroge jamais deux fois la même personne). Comme n (nombre de personnes interrogées) < A (population sondée)/10, cette approximation est légitime.

Voir aussi

Ce document provient de « Loi hyperg%C3%A9om%C3%A9trique ».

Catégorie : Loi de probabilité

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Loi Hypergéométrique de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

Loi hypergéométrique — Hypergéométrique Paramètres Support Densité de probabilité (fonction de masse) … Wikipédia en Français
Loi hypergeometrique — Loi hypergéométrique Hypergéométrique Densité de probabilité / Fonction de masse Fonction de répartition Paramètres … Wikipédia en Français
Loi hypergéometrique — Loi hypergéométrique Hypergéométrique Densité de probabilité / Fonction de masse Fonction de répartition Paramètres … Wikipédia en Français
Loi De Probabilité — Une loi de probabilité ou distribution de probabilité a commencé par décrire les répartitions typiques des fréquences d apparition des résultats d un phénomène aléatoire. Dans le dernier quart du XXe siècle, on a largement étendu le concept… … Wikipédia en Français
Loi de probabilite — Loi de probabilité Une loi de probabilité ou distribution de probabilité a commencé par décrire les répartitions typiques des fréquences d apparition des résultats d un phénomène aléatoire. Dans le dernier quart du XXe siècle, on a largement … Wikipédia en Français
Loi log-normale — Densité de probabilité / Fonction de masse μ=0 Fonction de répartition μ=0 … Wikipédia en Français
Loi logistique — Densité de probabilité / Fonction de masse Fonction de répartition … Wikipédia en Français
Loi uniforme discrète — Densité de probabilité / Fonction de masse n=5 où n = b − a + 1 Fonction de répartition … Wikipédia en Français
Loi de Bernoulli — Pour les articles homonymes, voir Théorème de Bernoulli. Bernoulli Paramètres (nombre réel) Support … Wikipédia en Français
Loi de probabilité — En théorie des probabilités et en statistique, une loi de probabilité décrit soit les probabilités de chaque valeur d une variable aléatoire (quand la variable aléatoire est discrète), soit la probabilité que la variable aléatoire appartienne à… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Loi Hypergéométrique