Loi de Fisher

Loi de Fisher
Fisher-Snedecor
Densité de probabilité / Fonction de masse
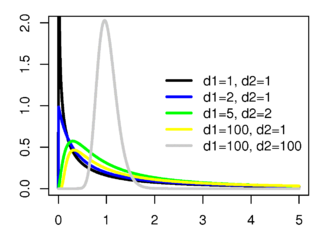
F distributionPDF.png
Fonction de répartition
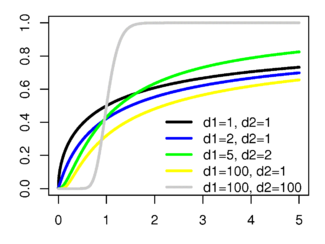
F distributionCDF.png
Paramètres d_1>0,\ d_2>0 degré de liberté
Support x \in [0, +\infty[\!
Densité de probabilité (fonction de masse) \frac{\sqrt{\frac{(d_1\,x)^{d_1}\,\,d_2^{d_2}} {(d_1\,x+d_2)^{d_1+d_2}}}} {x\,\mathrm{B}\!\left(\frac{d_1}{2},\frac{d_2}{2}\right)}\!
Fonction de répartition I_{\frac{d_1 x}{d_1 x + d_2}}(d_1/2, d_2/2)\!
Espérance \frac{d_2}{d_2-2}\! pour d2 > 2
Mode \frac{d_1-2}{d_1}\;\frac{d_2}{d_2+2}\! pour d1 > 2
Variance \frac{2\,d_2^2\,(d_1+d_2-2)}{d_1 (d_2-2)^2 (d_2-4)}\! pour d2 > 4
Asymétrie \frac{(2 d_1 + d_2 - 2) \sqrt{8 (d_2-4)}}{(d_2-6) \sqrt{d_1 (d_1 + d_2 -2)}}\! pour d2 > 6
Kurtosis normalisé 12\frac{d_1(5d_2-22)(d_1+d_2-2)+(d_2-4)(d_2-2)^2}{d_1(d_2-6)(d_2-8)(d_1+d_2-2)} pour d2 > 8
modifier Consultez la documentation du modèle

En théorie des probabilités et en statistiques, la loi de Fisher ou encore loi de Fisher-Snedecor ou encore loi F de Snedecor est une loi de probabilité continue[1],[2],[3]. Elle tire son nom des statisticiens Ronald Aylmer Fisher et George W. Snedecor. La loi de Fisher survient très fréquemment en tant que distribution de l'hypothèse nulle dans des tests statistiques, comme par exemple les tests du ratio de vraisemblance ou encore dans l'analyse de la variance (ANOVA) via le test du F.

Sommaire

Caractérisation

Une variable aléatoire réelle distribuée selon la loi de Fisher peut être construite comme le quotient de deux variables aléatoires indépendantes, U1 et U2, distribuées chacune selon une loi du χ² et ajustées pour leurs nombre de degrés de liberté, respectivement d1 et d2 :

\mathrm{F}(d_1, d_2) \sim \frac{U_1/d_1}{U_2/d_2}

La densité de probabilité d'une loi de Fisher, F(d1, d2), est donnée par

f(x) = \frac{\left(\frac{d_1\,x}{d_1\,x + d_2}\right)^{d_1/2} \; \left(1-\frac{d_1\,x}{d_1\,x + d_2}\right)^{d_2/2}}{x\; \mathrm{B}(d_1/2, d_2/2)}

pour tout réel x ≥ 0, où d1 et d2 sont des entiers positifs et B est la fonction bêta.

La fonction de répartition associée est F(x)=I_{\frac{d_1 x}{d_1 x + d_2}}(d_1/2, d_2/2)

où I est la fonction bêta incomplète régularisée.

L'espérance, la variance valent respectivement

\frac{d_2}{d_2-2}\!

pour d2 > 2 et

\frac{2\,d_2^2\,(d_1+d_2-2)}{d_1 (d_2-2)^2 (d_2-4)}\!

pour d2 > 4. Pour d2 > 8, le kurtosis normalisé est \gamma_2 = 12\frac{d_1(5d_2-22)(d_1+d_2-2)+(d_2-4)(d_2-2)^2}{d_1(d_2-6)(d_2-8)(d_1+d_2-2)}.

Généralisation

Une généralisation de la loi de Fisher est la loi de Fisher non centrée.


Distributions associées et propriétés

  • Si \ X \sim \mathrm{F}(\nu_1, \nu_2) alors Y = \lim_{\nu_2 \to \infty} \nu_1 X est distribuée selon une loi du χ² \chi^2_{\nu_{1}};
  • La loi F(ν1,ν2) est équivalente à la loi T-square de Hotelling's (\nu_1(\nu_1+\nu_2-1)/\nu_2)\operatorname{T}^2(\nu_1,\nu_1+\nu_2-1);
  • Si X \sim \operatorname{F}(\nu_1,\nu_2), alors \frac{1}{X} \sim F(\nu_2,\nu_1);
  • Si X \sim \mathrm{t}(\nu)\! est distribuée selon une loi de Student alors X^2 \sim \operatorname{F}(1, \nu);
  • Si X \sim \operatorname{F}(\nu_1,\nu_2) et Y=\frac{\nu_1 X/\nu_2}{1+\nu_1 X/\nu_2} alors Y \sim \operatorname{Beta}(\nu_1/2,\nu_2/2) est distribuée selon une loi bêta;
  • Si \operatorname{Q}_X(p) est le quantile d'ordre p pour X\sim \operatorname{F}(\nu_1,\nu_2) et que \operatorname{Q}_Y(p) est le quantile d'ordre p pour Y\sim \operatorname{F}(\nu_2,\nu_1) alors \operatorname{Q}_X(p)=1/\operatorname{Q}_Y(p).

Notes et références

  1. ↑ (en) Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York, Dover Publications, 1972 (ISBN 978-0-486-61272-0) 
  2. ↑ NIST (2006). Engineering Statistics Handbook - F Distribution
  3. ↑ (en) Alexander Mood, Franklin A. Graybill, Duane C. Boes, Introduction to the Theory of Statistics (Third Edition, p. 246-249), McGraw-Hill, 1974 (ISBN 978-0-07-042864-5) 

Liens externes


v · Lois de probabilités
Lois discrètes
à support fini Loi de Bernoulli • Loi uniforme discrète • Loi binomiale • Loi hypergéométrique • Loi de Benford
à support dénombrable Loi géométrique • Loi de Poisson • Loi binomiale négative • Loi logarithmique
Lois continues
à support compact Loi uniforme continue • Loi triangulaire • Loi bêta
à support semi-infini Loi exponentielle • Loi Gamma • Loi du χ² • Loi de Fisher • Loi de Weibull • Loi de Rayleigh • Loi de Rice • Loi d'Erlang • Loi de Lévy • Loi inverse-gamma • Loi log-normale
à support infini Loi normale • Loi normale asymétrique • Loi de Cauchy • Loi de Laplace • Loi logistique • Loi de Student • Loi stable • Loi de Gumbel
v · Probabilités et statistiques
Théorie des probabilités Axiomes des probabilités • Espace probabilisable • Probabilité • Événement • Tribu • Indépendance
Probabilités élémentaires Moyenne • Espérance • Médiane • Variance • Écart type
Loi de probabilité Variable aléatoire • Loi de Bernoulli • Loi de Poisson • Loi uniforme • Loi normale • Loi de Student • Loi de Fisher • Variables iid
Convergence de lois Théorème central limite • Loi des grands nombres • Théorème de Borel-Cantelli
Calcul stochastique Marche aléatoire • Chaîne de Markov • Processus stochastique • Processus de Markov • Martingale • Mouvement brownien • Équation différentielle stochastique
Statistiques
Statistique descriptive Échantillon • Quantile • Intervalle de confiance • Représentations de données • Histogramme • Diagramme circulaire • Boîte à moustaches • Régression linéaire • Méthode des moindres carrés
Statistique mathématique Fonction de répartition empirique • Théorème de Glivenko-Cantelli • Inférence bayésienne
Tests statistiques Test d'hypothèse • Hypothèse statistique • Estimateur • Test du χ² • Test t • Test de Fisher
Applications Économétrie • Mécanique statistique • Jeu de hasard • Biomathématique • Mathématiques financières
  • Portail des probabilités et des statistiques Portail des probabilités et des statistiques

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Loi de Fisher de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Loi de Fisher-Snedecor — Loi de Fisher Fisher Snedecor Densité de probabilité / Fonction de masse Fonction de répartition …   Wikipédia en Français

  • Loi De Student — Densité de probabilité / Fonction de masse Fonction de répartition …   Wikipédia en Français

  • Loi de student — Densité de probabilité / Fonction de masse Fonction de répartition …   Wikipédia en Français

  • Loi log-normale — Densité de probabilité / Fonction de masse μ=0 Fonction de répartition μ=0 …   Wikipédia en Français

  • Loi uniforme discrète — Densité de probabilité / Fonction de masse n=5 où n = b − a + 1 Fonction de répartition …   Wikipédia en Français

  • Loi logistique — Densité de probabilité / Fonction de masse Fonction de répartition …   Wikipédia en Français

  • Loi de Student — Pour le test statistique, voir Test t. Loi de Student Densité de probabilité / Fonction de masse Fonction de répartition …   Wikipédia en Français

  • Loi binomiale — Binomiale Densité de probabilité / Fonction de masse Fonction de répartition …   Wikipédia en Français

  • Loi de Bernoulli — Pour les articles homonymes, voir Théorème de Bernoulli. Bernoulli Paramètres (nombre réel) Support …   Wikipédia en Français

  • Loi de Poisson — Pour les articles homonymes, voir Poisson (homonymie). Poisson Densité de probabilité / Fonction de masse L axe horizontal est l indice k. La fonction est seulement définie pour les valeurs entières de …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”