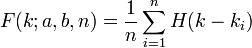Loi Uniforme Discrète

Loi uniforme discrète

**Loi uniforme discrète**
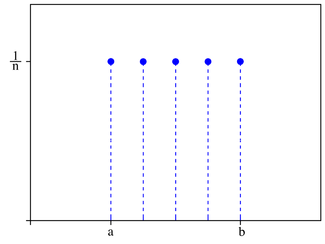
Densité de probabilité / Fonction de masse n=5 où $n = b - a + 1$
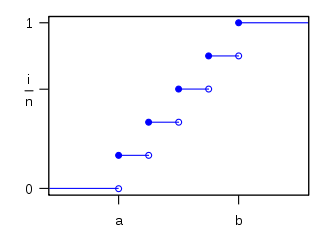
Fonction de répartition n=5 où $n = b - a + 1$ . Par convention la fonction de répartition (de masse) $F k (k i)$ est la probabilité que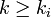 $k \ge k_i$
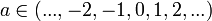
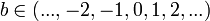
Paramètres	$a \in (...,-2,-1,0,1,2,...)\,$ $b \in (...,-2,-1,0,1,2,...)\,$ $n=b-a+1\,$
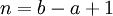
Support	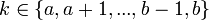$k \in \{a,a+1,...,b-1,b\}\,$
Densité de probabilité (fonction de masse)	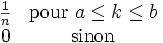$\begin{matrix} \frac{1}{n} & \mbox{pour }a\le k \le b\ \\0 & \mbox{sinon } \end{matrix}$
Fonction de répartition	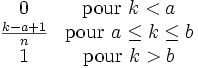$\begin{matrix} 0 & \mbox{pour }k<a\\ \frac{k-a+1}{n} & \mbox{pour }a \le k \le b \\1 & \mbox{pour }k>b \end{matrix}$
Espérance	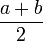$\frac{a+b}{2}\,$
Médiane (centre)	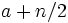$a+n/2\,$
Mode	N/A
Variance	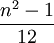$\frac{n^2-1}{12}\,$
Asymétrie (statistique)	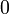$0\,$
Kurtosis (non-normalisé)	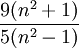$\frac{9(n^2+1)}{5(n^2-1)}\,$
Entropie	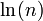$\ln(n)\,$
Fonction génératrice des moments	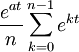$\frac{e^{at}}{n}\sum_{k=0}^{n-1}e^{kt}\,$
Fonction caractéristique	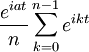$\frac{e^{iat}}{n}\sum_{k=0}^{n-1}e^{ikt}\,$

En théorie des probabilités, la loi discrète uniforme est une loi de probabilité discrète indiquant une probabilité de se réaliser identique (équiprobabilité) à chaque valeur d’un ensemble fini de valeurs possibles.

Description

Une variable aléatoire qui peut prendre $n$ valeurs possibles $k 1, k 2,..., k n$ équiprobables, suit une loi uniforme lorsque la probabilité de n’importe quelle valeur $k i$ est égale à $1 / n$ .

Un exemple simple de loi discrète uniforme est le lancer d’un dé honnête. Les valeurs possibles de $k$ sont 1, 2, 3, 4, 5, 6; et à chaque fois que le dé est lancé, la probabilité d’un score donné est égale à 1/6.

Dans le cas où les valeurs d’une variable aléatoire suivant une loi discrète uniforme sont réelles, il est possible d’exprimer la fonction de répartition en termes de distribution déterministe ; ainsi

$F(k;a,b,n)={1\over n}\sum_{i=1}^n H(k-k_i)$

où $H (x - x 0)$ désigne la fonction marche de Heaviside, est la fonction de répartition (ou distribution cumulative) de la distribution déterministe centrée en $x 0$ . Cela suppose que les hypothèses suffisantes soient vérifiées aux points de transition.

Voir aussi

Liens connexes

Loi uniforme continue

Portail des probabilités et des statistiques

Ce document provient de « Loi uniforme discr%C3%A8te ».

Catégorie : Loi de probabilité

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Loi Uniforme Discrète de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

Loi uniforme discrète — Densité de probabilité / Fonction de masse n=5 où n = b − a + 1 Fonction de répartition … Wikipédia en Français
Loi uniforme discrete — Loi uniforme discrète Loi uniforme discrète Densité de probabilité / Fonction de masse n=5 où n = b − a + 1 Fonction de répartition … Wikipédia en Français
Loi uniforme continue — Uniforme Densité de probabilité / Fonction de masse Fonction de répartition … Wikipédia en Français
Loi Uniforme Continue — Uniforme Densité de probabilité / Fonction de masse Fonction de répartition … Wikipédia en Français
Loi Uniforme — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. En mathématiques, les lois uniformes sont des lois de probabilité. Elles sont de types: La loi uniforme discrète la loi uniforme continue Ce document… … Wikipédia en Français
Loi uniforme — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. En mathématiques, les lois uniformes sont des lois de probabilité. Il en existe une version discrète et une continue : Loi uniforme discrète Loi… … Wikipédia en Français
Loi discrète uniforme — Loi uniforme discrète Loi uniforme discrète Densité de probabilité / Fonction de masse n=5 où n = b − a + 1 Fonction de répartition … Wikipédia en Français
Loi log-normale — Densité de probabilité / Fonction de masse μ=0 Fonction de répartition μ=0 … Wikipédia en Français
Loi logistique — Densité de probabilité / Fonction de masse Fonction de répartition … Wikipédia en Français
Loi de probabilité — En théorie des probabilités et en statistique, une loi de probabilité décrit soit les probabilités de chaque valeur d une variable aléatoire (quand la variable aléatoire est discrète), soit la probabilité que la variable aléatoire appartienne à… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Loi Uniforme Discrète