Distribution d'Erlang

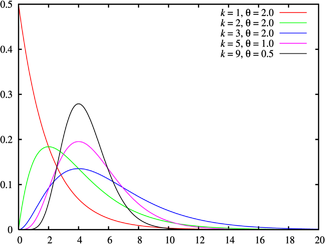
Erlang
Densité de probabilité / Fonction de masse
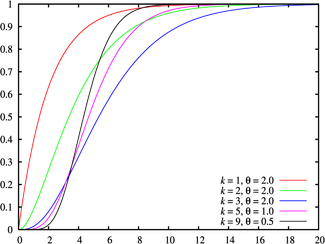
Fonction de répartition

Paramètres	$k > 0\,$ Paramètre de forme (entier) $\lambda > 0\,$ intensité (réel) alt.: $\theta = 1/\lambda > 0\,$ paramètre d'échelle (réel)
Support	$x \in [0; \infty)\!$
Densité de probabilité (fonction de masse)	$\frac{\lambda^k x^{k-1} e^{-\lambda x}}{(k-1)!\,}$
Fonction de répartition	$\frac{\gamma(k, \lambda x)}{(k-1)!}=1-\sum_{n=0}^{k-1}e^{-\lambda x}(\lambda x)^{n}/n!$
Espérance	$k/\lambda\,$
Médiane (centre)	pas de forme simple
Mode	$(k-1)/\lambda\,$ pour $k \geq 1\,$
Variance	$k /\lambda^2\,$
Asymétrie	$\frac{2}{\sqrt{k}}$
Kurtosis normalisé	$\frac{6}{k}$
Entropie	$k/\lambda+(k-1)\ln(\lambda)+\ln((k-1)!)\,$ $+(1-k)\psi(k)\,$
Fonction génératrice des moments	$(1 - t/\lambda)^{-k}\,$ pour $t < \lambda\,$
Fonction caractéristique	$(1 - it/\lambda)^{-k}\,$
modifier

La distribution d'Erlang est une loi de probabilité continue, dont l'intérêt est dû à sa relation avec les distributions exponentielle et Gamma. Cette distribution a été développée par Agner Krarup Erlang afin de modéliser le nombre d'appels téléphoniques simultanés.

Sommaire

1 Généralité
2 Caractérisation
- 2.1 Densité de probabilité
- 2.2 Fonction de répartition
3 Occurrence
- 3.1 Temps d'attente
- 3.2 Processus stochastiques
4 Voir aussi
5 Liens externes

Généralité

La distribution est continue et possède deux paramètres: le paramètre de forme $k$ , un entier, et le paramètre d'intensité $λ$ , un réel. On utilise parfois une paramétrisation alternative, où on considère plutôt le paramètre d'échelle $θ = 1 / λ$ .

Lorsque le paramètre de forme $k$ vaut 1, la distribution se simplifie en la loi exponentielle.

La distribution d'Erlang est un cas spécial de la distribution Gamma, où le paramètre de forme $k$ est un entier. Dans la loi Gamma, ce paramètre est réel positif.

Caractérisation

Densité de probabilité

La Densité de probabilité de la distribution d'Erlang est

$f(x; k,\lambda)={\lambda^k x^{k-1} \exp(-\lambda x) \over (k-1)!}\quad\mbox{pour }x>0.$

Le paramètre $k$ est le paramètre de forme, et $λ$ le paramètre d'intensité. Une paramétrisation équivalente met en jeu le paramètre d'échelle $θ$ , défini comme l'inverse de l'intensité (c'est-à-dire $θ = 1 / λ$ ):

$f(x; k,\theta)=\frac{ x^{k-1} \exp(-\frac{x}{\theta} )}{\theta^k(k-1)!}\quad\mbox{pour }x>0.$

La présence de la factorielle implique que k doit être un entier naturel.

Fonction de répartition

La Fonction de répartition de la distribution d'Erlang est

$F(x; k,\lambda) = \frac{\gamma(k, \lambda x)}{(k-1)!}$

où $γ()$ est la fonction gamma incomplète. Cette fonction peut aussi s'écrire:

$F(x; k,\lambda) = 1-\sum_{n=0}^{k-1}e^{-\lambda x} \frac{(\lambda x)^{n}}{n!}$

Occurrence

Temps d'attente

Les événements qui se produisent avec une intensité moyenne donnée, sont modélisés par un processus de Poisson. Les temps d'attente entre k occurrences sont distribués selon une distribution d'Erlang. La question associée du dénombrement des événements dans un laps de temps donné est décrite par la loi de Poisson.

Processus stochastiques

La distribution d'Erlang est aussi la distribution de la somme de k variables aléatoires i.i.d. (indépendamment et identiquement distribuées) selon une loi exponentielle.

Voir aussi

Processus de Poisson

Liens externes

v · Lois de probabilités

Lois discrètes

à support fini	Loi de Bernoulli • Loi uniforme discrète • Loi binomiale • Loi hypergéométrique • Loi de Benford
à support dénombrable	Loi géométrique • Loi de Poisson • Loi binomiale négative • Loi logarithmique

Lois continues

à support compact	Loi uniforme continue • Loi triangulaire • Loi bêta
à support semi-infini	Loi exponentielle • Loi Gamma • Loi du χ² • Loi de Fisher • Loi de Weibull • Loi de Rayleigh • Loi de Rice • Loi d'Erlang • Loi de Lévy • Loi inverse-gamma • Loi log-normale
à support infini	Loi normale • Loi normale asymétrique • Loi de Cauchy • Loi de Laplace • Loi logistique • Loi de Student • Loi stable • Loi de Gumbel

Portail des probabilités et des statistiques

Catégorie :

Loi de probabilité

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Distribution d'Erlang de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

Erlang (programming language) — Erlang Paradigm(s) multi paradigm: concurrent, functional Appeared in 1986 Designed by Ericsson … Wikipedia
Erlang distribution — Probability distribution name =Erlang type =density pdf cdf parameters =k > 0 in mathbb{Z} shape lambda > 0, rate (real) alt.: heta = 1/lambda > 0, scale (real) support =x in [0; infty)! pdf =frac{lambda^k x^{k 1} e^{ lambda x{(k 1)!,} cdf… … Wikipedia
Distribution Gamma — Loi Gamma Densité de probabilité / Fonction de masse Fonction de répartition > … Wikipédia en Français
Erlang (Langage) — Pour les articles homonymes, voir Erlang. Apparu en 1987 … Wikipédia en Français
Erlang (langage de programmation) — Erlang (langage) Pour les articles homonymes, voir Erlang. Apparu en 1987 … Wikipédia en Français
Erlang langage de programmation — Erlang (langage) Pour les articles homonymes, voir Erlang. Apparu en 1987 … Wikipédia en Français
Erlang — may refer to: * Agner Krarup Erlang, a mathematician and engineer after whom several concepts are named ** Erlang unit, a unit to measure traffic in telecommunications or other domains ** Erlang distribution, a probability distribution describing … Wikipedia
Erlang-B — (sometimes also written without the hyphen Erlang B) is a formula derived from the Erlang distribution to describe the probability of call loss on a group of circuits (in a circuit switched network, or equivalent). It is, for example, used in… … Wikipedia
Distribution de Lévy — Densité de probabilité / Fonction de masse Fonction de répartition … Wikipédia en Français
Erlang unit — The erlang (symbol E [ [http://www.unc.edu/ rowlett/units/dictE.html How Many? A Dictionary of Units of Measurement] ] ) as a dimensionless unit is used in telephony as a statistical measure of the volume of telecommunications traffic. It is… … Wikipedia

Dictionnaires et Encyclopédies sur 'Academic'

Distribution d'Erlang

Sommaire

Généralité