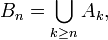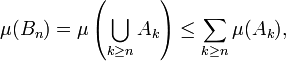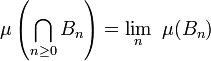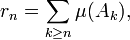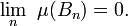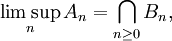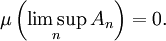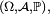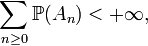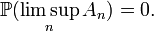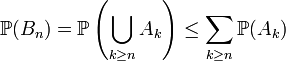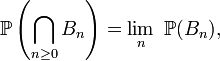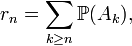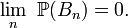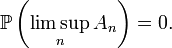Theoreme de Borel-Cantelli

Theoreme de Borel-Cantelli

Théorème de Borel-Cantelli

Sommaire

Introduction

Dans la théorie des probabilités, le lemme de Borel-Cantelli, parfois aussi appelé théorème de Borel-Cantelli, concerne une suite d'événements. Sous une forme un peu plus générale, il est également valable en théorie de la mesure. Le lemme stipule que :

Lemme de Borel-Cantelli — Si la somme des probabilités d'une suite 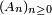\scriptstyle\ (A_n)_{n\ge 0} d'événements d'un espace probabilisé 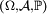\scriptstyle\ \left(\Omega, \mathcal A, \mathbb{P}\right)\ est finie, alors la probabilité qu'une infinité d'entre eux se réalisent simultanément est nulle.

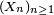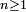L'indépendance des événements n'est pas nécessaire. Par exemple, considérons une suite \scriptstyle\ (X_n)_{n\ge 1} de variables aléatoires, telle que, pour tout \scriptstyle\ n\ge 1,

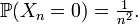
\textstyle \mathbb{P}(X_n= 0) = \frac1{n^2}.

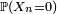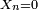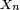La somme des \scriptstyle\ \mathbb{P}(X_n = 0) est finie[1], donc d'après le lemme de Borel-Cantelli la probabilité que \scriptstyle\ X_n = 0 se produise pour une infinité d'indices \scriptstyle\ n est 0. En d'autres termes, avec une probabilité de 1, \scriptstyle\ X_n est non nul à partir d'un certain rang (aléatoire) 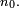\scriptstyle\ n_0. On a donc appliqué le lemme de Borel-Cantelli à la suite d'évènements 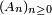\scriptstyle\ (A_n)_{n\ge 0} définie par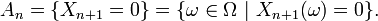

\textstyle A_n=\{X_{n+1}= 0\} =\{\omega\in\Omega\ |\ X_{n+1}(\omega)= 0\}.

Limite supérieure d'ensembles

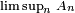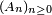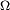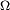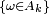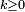Définition —  La limite supérieure \scriptstyle \limsup_n\, A_n d'une suite \scriptstyle\ (A_n)_{n\ge 0}\, de parties d'un ensemble \scriptstyle \Omega est l'ensemble des éléments \scriptstyle \omega de \scriptstyle \Omega tels que l'assertion \scriptstyle \{\omega\in A_k\} soit vérifiée pour une infinité d'indices \scriptstyle k\ge 0.

En d'autres termes, on peut dire que 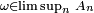\scriptstyle\ \omega\in\limsup_n\, A_n si et seulement si l'ensemble 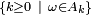\scriptstyle \{k\ge 0\ \vert\ \omega\in A_k\} est infini, ou bien non borné. Une formulation équivalente est la suivante : pour tout 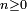\scriptstyle n\ge 0, on peut trouver 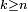\scriptstyle k\ge n tel que 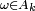\scriptstyle \omega\in A_k. Cette dernière formulation fournit une écriture commode de la limite supérieure d'ensembles à l'aide d'opérations élémentaires sur les ensembles :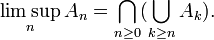

\limsup_n A_n =\bigcap_{n\ge 0}(\bigcup_{k\ge n} A_k).

Sous l'influence de la terminologie anglo-saxonne, on dira aussi parfois que 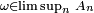\scriptstyle\ \omega\in\limsup_n\, A_n si et seulement si 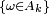\scriptstyle\ \{\omega\in A_k\}\ "infiniment souvent" ou bien "infinitely often", d'où la notation rencontrée dans certains ouvrages :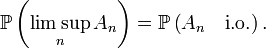

\mathbb{P}\left(\limsup_n A_n\right)=\mathbb{P}\left(A_n\quad\text{i.o.}\right).

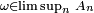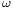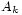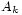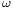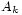Finalement, remarquons que la définition "\scriptstyle\ \omega\in\limsup_n\, A_n si et seulement si \scriptstyle\ \omega\ appartient à une infinité de \scriptstyle\ A_k\ " peut induire en erreur : si par exemple toutes les parties \scriptstyle\ A_k\ sont égales, il se peut que \scriptstyle\ \omega\ appartienne à \scriptstyle\ A_k\ pour une infinité d'indices \scriptstyle\ k\ , et il se peut donc que \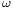scriptstyle\ \omega\ appartienne à \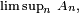scriptstyle\ \limsup_n\, A_n, sans pour autant qu'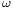\scriptstyle\ \omega\ appartienne à une infinité de 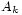\scriptstyle\ A_k\ (puisqu'il n'existe, au fond, qu'un seul \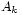scriptstyle\ A_k).

Théorème de Borel-Cantelli (théorie de la mesure)

Pour un espace mesuré général 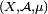\scriptstyle\ (X,\mathcal{A},\mu), le lemme de Borel-Cantelli prend la forme suivante :

Théorème de Borel-Cantelli — Soit 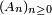\scriptstyle\ (A_n)_{n\ge 0} une suite dans 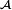\scriptstyle\ \mathcal{A}. Si

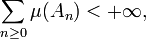
\sum_{n\ge 0}\mu(A_n)<+\infty,

alors

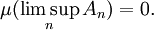\mu(\limsup_n A_n) = 0.
Démonstration

Posons

B_n=\bigcup_{k\ge n}A_k,

et remarquons que

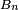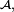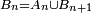  • \scriptstyle\ B_n\ est une suite décroissante (pour l'inclusion) d'éléments de \scriptstyle\ \mathcal{A}, car \scriptstyle\ B_n= A_n\cup B_{n+1} ;
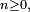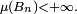
  • pour tout \scriptstyle\ n\ge 0, on a \scriptstyle\ \mu(B_n)<+\infty.

Le deuxième point découle de la majoration

\mu(B_n)=\mu\left(\bigcup_{k\ge n}A_k\right)\le\sum_{k\ge n}\mu(A_k),

et de l'hypothèse du théorème de Borel-Cantelli, selon laquelle 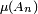\scriptstyle\ \mu(A_n)\ est le terme général d'une série convergente. Les 2 conditions permettant de conclure que

\mu\left(\bigcap_{n\ge 0}B_n\right)=\lim_n\ \mu(B_n)

sont ainsi remplies. De plus 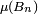\scriptstyle\ \mu(B_n)\ est majorée par

r_n=\sum_{k\ge n}\mu(A_k),

qui est le reste d'une série convergente, donc

\lim_n\ \mu(B_n)=0.

Comme

\limsup_n A_n=\bigcap_{n\ge 0}B_n,

on conclut que

\mu\left(\limsup_n A_n\right)=0.

CQFD

Lemme de Borel-Cantelli (probabilités)

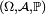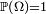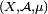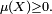Un espace probabilisé \scriptstyle\ \left(\Omega, \mathcal A, \mathbb{P}\right) est un cas particulier d'espace mesuré, en ce qu'on suppose, de plus, que \scriptstyle\ \mathbb{P}\left(\Omega\right)=1, alors que la seule restriction du même ordre sur \scriptstyle\ (X,\mathcal{A},\mu) est \scriptstyle\ \mu(X)\ge 0. En particulier, le lemme de Borel-Cantelli donné en introduction est une forme affaiblie du théorème de Borel-Cantelli donné à la section précédente. Peut-être le lemme de Borel-Cantelli est-il plus populaire en probabilités, où il est crucial dans la démonstration, par Kolmogorov, de la loi forte des grands nombres (s'il ne faut donner qu'un seul exemple). Dans le cadre probabiliste, une formulation plus formelle du lemme donné en langage intuitif dans l'introduction pourrait donc s'écrire :

Lemme de Borel-Cantelli — Dans un espace probabilisé \scriptstyle\ \left(\Omega, \mathcal A, \mathbb{P}\right), considérons une suite \scriptstyle\ (A_n)_{n\ge 0} d'éléments de \scriptstyle\ \mathcal{A}. Si

\sum_{n\ge 0}\mathbb{P}(A_n)<+\infty,

alors

\mathbb{P}(\limsup_n A_n) = 0.
Démonstration

La démonstration est en tout point identique à celle du théorème précédent. On pose

B_n=\bigcup_{k\ge n}A_k,

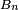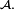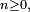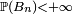et on remarque que \scriptstyle\ B_n\ est une suite décroissante (pour l'inclusion) d'éléments de \scriptstyle\ \mathcal{A}. La condition "pour tout \scriptstyle\ n\ge 0, on a \scriptstyle\ \mathbb{P}(B_n)<+\infty" est ici automatiquement remplie. La majoration

\mathbb{P}(B_n)=\mathbb{P}\left(\bigcup_{k\ge n}A_k\right)\le\sum_{k\ge n}\mathbb{P}(A_k)

reste vraie, mais n'est pas utile pour démontrer que

\mathbb{P}\left(\bigcap_{n\ge 0}B_n\right)=\lim_n\ \mathbb{P}(B_n),

propriété vraie, en probabilités, pour toute suite décroissante d'évènements. Par contre la majoration de 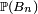\scriptstyle\ \mathbb{P}(B_n)\ par le reste

r_n=\sum_{k\ge n}\mathbb{P}(A_k),

d'une série convergente est toujours indispensable pour conclure que

\lim_n\ \mathbb{P}(B_n)=0.

On termine de la même manière que dans le cas général, à l'aide

\limsup_n A_n=\bigcap_{n\ge 0}B_n,

pour conclure que

\mathbb{P}\left(\limsup_n A_n\right)=0.

CQFD

Loi du zéro-un de Borel

Le lemme de Borel-Cantelli ne doit pas être confondu avec la loi du zéro-un de Borel, parfois appelée second lemme de Borel-Cantelli :

Loi du zéro-un de Borel — Si les événements 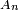\scriptstyle\ A_n sont indépendants, alors 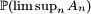\scriptstyle\ \mathbb{P}\left(\limsup_n A_n\right) vaut 0 ou 1 suivant que la série de terme général 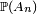\scriptstyle\ \mathbb{P}(A_n) est convergente ou divergente.

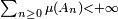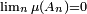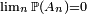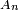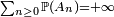La loi du zéro-un de Borel[2] montre en particulier que l'hypothèse \scriptstyle\ \sum_{n\ge 0}\mu(A_n)<+\infty du lemme de Borel-Cantelli ne peut en aucun cas être affaiblie en \scriptstyle\ \lim_{n}\mu(A_n)=0. En effet on peut avoir simultanément, d'une part \scriptstyle\ \lim_{n}\mathbb{P}(A_n)=0, d'autre part (indépendance des \scriptstyle\ A_n et \scriptstyle\ \sum_{n\ge 0}\mathbb{P}(A_n)=+\infty), donc on peut avoir simultanément :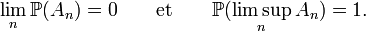

\lim_{n}\mathbb{P}(A_n)=0\qquad\text{et}\qquad \mathbb{P}(\limsup_n A_n) = 1.

Notes et références

  1. ↑ En fait elle vaut 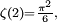\scriptstyle\ \zeta(2)=\frac{\pi^2}6, voir l'article Fonction zêta de Riemann, par exemple la section Valeurs numériques particulières.
  2. ↑ La loi du zéro-un de Borel a été publiée en 1909 dans l'article Les probabilités dénombrables et leurs applications arithmétiques. Rend. Circ. Math. Palermo 27, pp. 247-271, par Emile Borel, en vue, semble-t-il, d'applications aux propriétés des fractions continues. Il semble que ce n'est qu'un peu plus tard que Cantelli a remarqué et utilisé le fait que, pour l'un des deux sens, l'hypothèse d'indépendance est superflue (à vérifier).

Voir aussi


  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9or%C3%A8me de Borel-Cantelli ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme de Borel-Cantelli de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

  • Théorème de borel-cantelli — Sommaire 1 Introduction 2 Limite supérieure d ensembles 3 Théorème de Borel Cantelli (théorie de la mesure) 4 …   Wikipédia en Français

  • Théorème de Borel-Cantelli —  Ne doit pas être confondu avec Théorème de Borel ni Lemme de Borel Carathéodory. Le théorème de Borel Cantelli ou lemme de Borel Cantelli, nommé d après les mathématiciens Émile Borel et Francesco Paolo Cantelli, est un résultat de théorie… …   Wikipédia en Français

  • Théorème de Glivenko-Cantelli — Le théorème de Glivenko Cantelli est parfois appelé « le théorème fondamental de la statistique » car il exprime en quoi une loi de probabilité peut être révélée par la connaissance d un (grand) échantillon de ladite loi de probabilité …   Wikipédia en Français

  • Théorème de Borel —  Ne doit pas être confondu avec Théorème de Borel Cantelli ni Théorème de Borel Lebesgue. En mathématiques, le théorème de Borel[1],[2] …   Wikipédia en Français

  • Lemme de Borel-Cantelli — Théorème de Borel Cantelli Sommaire 1 Introduction 2 Limite supérieure d ensembles 3 Théorème de Borel Cantelli (théorie de la mesure) 4 …   Wikipédia en Français

  • Théorème central limite — Pour les articles homonymes, voir TCL. La loi normale, souvent appelée la « courbe en cloche » Le théorème central li …   Wikipédia en Français

  • Théorème d'arrêt de Doob — Le théorème d arrêt de Doob est dû à Joseph Leo Doob. Énoncé On considère un processus stochastique Théorème    (a) Supposons que X est une surmartingale, et que T est un temps d arrêt. Alors, dès que l un des 3 ensembles d hypothèses… …   Wikipédia en Français

  • Théorème de Darmois — Énoncé Soit une variable X dont le domaine de définition ne dépend pas de θ Une condition nécessaire et suffisante pour que l échantillon (X1,...,Xn) admette une statistique exhaustive est que la forme de la densité soit : (famille… …   Wikipédia en Français

  • Émile Borel — Pour les articles homonymes, voir Borel. Émile Borel Émile Borel (1932) …   Wikipédia en Français

  • Emile Borel — Émile Borel Pour les articles homonymes, voir Borel. Émile Borel …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”