Espace Probabilisable
- Espace Probabilisable
-
Espace probabilisable
Un espace probabilisable est un couple 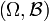 formé d'un ensemble Ω, d'une tribu ou σ-algèbre
formé d'un ensemble Ω, d'une tribu ou σ-algèbre 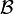 sur Ω.
sur Ω.
L'ensemble Ω est appelé l'univers et les éléments de 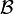 sont appelés les évènements.
sont appelés les évènements.
Exemples :
- Soit Ω un univers quelconque ;
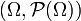 est un espace probabilisable. Cet exemple est important puisque si Ω est fini ou dénombrable alors la tribu engendrée par les évènements élémentaires est égale à
est un espace probabilisable. Cet exemple est important puisque si Ω est fini ou dénombrable alors la tribu engendrée par les évènements élémentaires est égale à 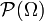 (l'ensemble des parties de Ω).
(l'ensemble des parties de Ω).
- Soit Ω un univers quelconque;
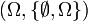 est un espace probabilisable (
est un espace probabilisable (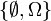 est la tribu grossière).
est la tribu grossière).
- Lorsque Ω est un espace topologique, on utilise fréquemment l'espace probabilisable
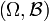 , où
, où 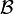 est la tribu borélienne sur Ω.
est la tribu borélienne sur Ω.
Dans la pratique, l'univers Ω se définit en fonction de l'expérience aléatoire 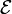 effectuée, et la tribu se choisit en fonction des évènements concernés par le problème.
effectuée, et la tribu se choisit en fonction des évènements concernés par le problème.
Si nous décidons de travailler dans la tribu grossière, nous ne pourrons considérer que l'évènement certain et l'évènement impossible. Lorsque l'univers est fini ou dénombrable, on choisit le plus souvent la tribu discrète : 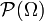 .
.
Lorsque, sur un espace probabilisable, on définit une probabilité, l'espace probabilisable devient un espace probabilisé.
|
Articles de mathématiques en rapport avec les probabilités ou les statistiques |
|
|
 Portail des probabilités et des statistiques
Portail des probabilités et des statistiques
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Espace Probabilisable de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Espace probabilisable — ● Espace probabilisable couple formé d un ensemble Ω et d une tribu A de parties de Ω, dont les éléments sont les événements de l espace probabilisable. (A est une algèbre d événements sur Ω.) … Encyclopédie Universelle
Espace probabilisable — Un espace probabilisable est un couple formé d un ensemble Ω, d une tribu ou σ algèbre sur Ω. L ensemble Ω est appelé l univers et les éléments de sont appelés les évènements. Exemples : Soit Ω un univers quelconque ; est un espace… … Wikipédia en Français
Probabilité sur un espace probabilisable — ● Probabilité sur un espace probabilisable mesure positive P sur (Ω, A) définie de A dans [0, 1] et vérifiant les axiomes (dits de Kolmogorov) : (1) P(Ω) = 1 ; (2) pour tout couple d événements incompatibles de A, P(A ∪ B) = P(A) + P(B) ; (3)… … Encyclopédie Universelle
probabilisable — ● probabilisable adjectif Espace probabilisable, couple formé d un ensemble Ω et d une tribu A de parties de Ω, dont les éléments sont les événements de l espace probabilisable. (A est une algèbre d événements sur Ω.) ● probabilisable… … Encyclopédie Universelle
Espace Mesurable — Soit X un ensemble et une tribu sur X. On appelle espace mesurable le couple . Les éléments de sont appelés ensembles mesurables. Espace mesuré Soit … Wikipédia en Français
Espace Probabilisé — Un espace de probabilité(s)[1] ou espace probabilisé est la donnée d une probabilité à tout événement tangible . Formellement, c est un triplet formé d un ensemble Ω, d une tribu ou σ algèbre sur Ω et d une mesure P sur cette σ algèbre telle que… … Wikipédia en Français
Espace de probabilité — Espace probabilisé Un espace de probabilité(s)[1] ou espace probabilisé est la donnée d une probabilité à tout événement tangible . Formellement, c est un triplet formé d un ensemble Ω, d une tribu ou σ algèbre sur Ω et d une mesure P sur cette σ … Wikipédia en Français
Espace probabilise — Espace probabilisé Un espace de probabilité(s)[1] ou espace probabilisé est la donnée d une probabilité à tout événement tangible . Formellement, c est un triplet formé d un ensemble Ω, d une tribu ou σ algèbre sur Ω et d une mesure P sur cette σ … Wikipédia en Français
Espace probabilisé — Un espace de probabilité(s)[1] ou espace probabilisé est la donnée d une probabilité à tout événement tangible . Formellement, c est un triplet formé d un ensemble Ω, d une tribu ou σ algèbre sur Ω et d une mesure P sur cette σ algèbre telle que… … Wikipédia en Français
Variable régionalisée — La VR comme phénomène physique : topographie de la ville de Binche … Wikipédia en Français
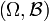 formé d'un ensemble Ω, d'une tribu ou σ-algèbre
formé d'un ensemble Ω, d'une tribu ou σ-algèbre 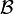 sur Ω.
sur Ω.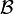 sont appelés les évènements.
sont appelés les évènements.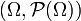 est un espace probabilisable. Cet exemple est important puisque si Ω est fini ou dénombrable alors la tribu engendrée par les évènements élémentaires est égale à
est un espace probabilisable. Cet exemple est important puisque si Ω est fini ou dénombrable alors la tribu engendrée par les évènements élémentaires est égale à 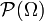 (l'ensemble des parties de Ω).
(l'ensemble des parties de Ω).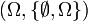 est un espace probabilisable (
est un espace probabilisable (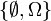 est la tribu grossière).
est la tribu grossière).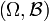 , où
, où  est la tribu borélienne sur Ω.
est la tribu borélienne sur Ω.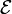 effectuée, et la tribu se choisit en fonction des évènements concernés par le problème.
effectuée, et la tribu se choisit en fonction des évènements concernés par le problème.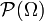 .
.