Loi de probabilité

Loi de probabilité

En théorie des probabilités et en statistique, une loi de probabilité décrit soit les probabilités de chaque valeur d'une variable aléatoire (quand la variable aléatoire est discrète), soit la probabilité que la variable aléatoire appartienne à un intervalle arbitraire (quand la variable est continue)[1]. La loi de probabilité décrit l'ensemble des valeurs qu'une variable aléatoire peut atteindre et la probabilité que la valeur de la variable aléatoire soit dans n'importe quel sous ensemble (mesurable) de cet ensemble.

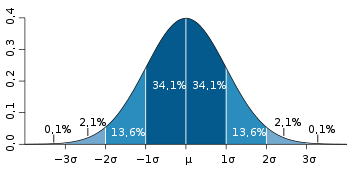La loi normale, souvent appelée la « courbe en cloche »

Quand la variable aléatoire prend ses valeurs dans \scriptstyle\ \mathbb{R},\ la loi de probabilité est complètement déterminée par sa fonction de répartition, dont la valeur en chaque réel x est la probabilité que la variable aléatoire soit inférieure ou égale à x.

Le concept de loi de probabilité (et le concept de variable aléatoire) sont les fondements des disciplines mathématiques appelées théorie des probabilités, et statistique. Il y a de la fluctuation ou de la variabilité dans presque toute valeur qui peut être mesurée dans une population (par exemple la taille des individus, la durabilité d'une pièce de métal, etc.) ; presque toutes les mesures ont une part d'erreur intrinsèque ; en physique, de nombreux processus ont une description probabiliste, de la théorie cinétique des gaz à la description quantique des particules élémentaires. Pour ces raisons en particulier, et pour beaucoup d'autres raisons, de simples nombres sont souvent inadéquats pour décrire une quantité, alors qu'une loi de probabilité est plus appropriée.

Bien des lois de probabilités apparaissent dans les applications. Une des plus importantes est la loi normale, qui est aussi connue sous le nom de distribution gaussienne ou de courbe en cloche et qui approxime de nombreuses lois de probabilités apparaissant dans les applications. Le jet d'une pièce donne lieu à une autre loi de probabilité naturelle, dont les valeurs possibles sont pile ou face, chacune avec probabilité 1/2.

Sommaire

Définition informelle

Une loi de probabilité se caractérise de différentes manières. Le plus souvent, on utilise la fonction de répartition pour caractériser une loi. Cela présente l'avantage d'être valable aussi bien pour les lois discrètes que continues. Dans le cas d'une loi continue, on utilise très souvent la densité, alors que dans le cas discret, la donnée des probabilités élémentaires suffit à caractériser la loi en question.

Exemples de lois discrètes

Une variable aléatoire X est discrète si l'ensemble de ses valeurs possibles est fini ou dénombrable. On dit alors que sa loi est discrète. Pour une définition plus formelle, voir la section "Classification des lois de probabilités sur la droite réelle". Pour la plupart des lois discrètes classiques, les valeurs possibles de X sont des entiers naturels. On définit alors la loi discrète en donnant la probabilité que X prenne chaque valeur entière possible n, soit

\ P(X = n) ou \ \mathbb{P}(X = n).

Loi uniforme discrète

Article détaillé : Loi uniforme discrète.

La loi uniforme discrète correspond à des événements équiprobables (exemple : lancer de dés, n=6 ) :

  • \ P(X = 1) = P(X = 2) = ... = P(X = n)=1/n
  • \ \mathbb{E}(X) = \frac{n+1}{2}
  • \ V(X) = \frac{n^2-1}{12}

Loi de Bernoulli

Article détaillé : Loi de Bernoulli.

La loi de Bernoulli correspond à une expérience à deux issues (succès - échec), codées resp. par les valeurs 1, 0, et en général non équiprobables :

  • \ P(X = 1) = p où p est la probabilité de succès
  • \ P(X = 0) = q où q = 1-p est la probabilité d'échec
  • \ \mathbb{E}(X) = p
  • \ V(X) = p(1-p) = pq

Loi binomiale

Article détaillé : Loi binomiale.

C'est la loi du nombre de succès obtenus à l'issue de n épreuves de Bernoulli indépendantes de paramètre p.

  • P(X = k)={n\choose k} p^k(1-p)^{n-k} pour tout k de 0 à n, p étant un réel compris entre 0 et 1
  • \ \mathbb{E}(X) = np
  • \ V(X) = np(1- p) = npq où q = 1 − p

Loi hypergéométrique

Article détaillé : Loi hypergéométrique.

On tire simultanément n boules dans une urne contenant pA boules gagnantes et qA boules perdantes (avec q = 1 - p, soit un nombre total de boules valant pA + qA = A). On compte alors le nombre de boules gagnantes extraites et on appelle X la variable aléatoire donnant le nombre de boules gagnantes.

  • P(X = k) = \frac{{pA\choose k}{(1-p)A\choose n-k}}{{A\choose n}} où A est un entier, pA et n des entiers inférieurs à A
  • \ \mathbb{E}(X)=np
  • V(X) = np(1-p)\frac{A-n}{A - 1}

Loi de Poisson

Article détaillé : Loi de Poisson.
  • P(X = k) = \frac{\lambda ^ k}{k!} \exp (-\lambda)\qquad k \in \mathbb{N},\ \lambda \in \mathbb{R}_+^*
  • \ \mathbb{E}(X) = \lambda
  • \ V(X) = \lambda

Loi géométrique

Article détaillé : Loi géométrique.

On considère une épreuve de Bernoulli dont la probabilité de succès est p et celle d'échec q = 1 - p.

On renouvelle cette épreuve de manière indépendante jusqu'au premier succès. On appelle X la variable aléatoire donnant le rang du premier succès.

  • \ P(X = n)=(1-p)^{n-1}p, \ n\in \mathbb{N}^*
  • \ \mathbb{E}(X) = \frac{1}{p}
  • \ V(X) = \frac{1-p}{p^2}

Exemples de lois à densité

Article détaillé : Densité de probabilité.

Une variable aléatoire réelle \scriptstyle\ X\ possède une densité de probabilité \scriptstyle\ f_X\ , si pour tous nombres réels \scriptstyle\ a<b\ on a

\mathbb{P}(a < X < b) = \int_a^b f_X(x)\, \textrm{d}x.

On dit aussi alors que la loi \scriptstyle\ \mathbb{P}_X\ de \scriptstyle\ X\ possède une densité, ou bien est à densité. D'une manière équivalente, on dit que \scriptstyle\ \mathbb{P}_X\ est absolument continue par rapport à la mesure de Lebesgue.

En conséquence, \scriptstyle\ \mathbb{P}(X=a) = 0, pour tout nombre réel \scriptstyle\ a, et la fonction de répartition \scriptstyle\ F_X\ de \scriptstyle\ X\ est continue. On a plus précisément

F_X(x) = \int_{-\infty}^x f_X(u)\, \textrm{d}u.

Les variables aléatoires à densité sont parfois appelées variables continues.

Loi uniforme

Article détaillé : Loi uniforme continue.

Loi uniforme continue sur un intervalle borné [a; b] :

  • f_X (x) = \left\{\begin{matrix} \frac{1}{b-a}& \mathrm{si}\ x \in [a;b] \\ 0& \mathrm{sinon} \end{matrix}\right.
  • \mathbb{E}(X) = \frac{a+b}{2}
  • V(X) = \frac{(b-a)^2}{12}

Loi normale

Article détaillé : Loi normale.
  • f_X (x) = \frac{1}{\sigma\sqrt{2\pi}} \cdot e^{ \left ( - \frac{(x-m)^2}{2 \sigma^2} \right )} \ \ , \sigma \ge 0
  • \ \mathbb{E}(X) = m
  • \ V(X) = \sigma^2

Loi exponentielle

Article détaillé : Loi exponentielle.
  • f_X (x) = \left\{\begin{matrix} \lambda.\exp(-\lambda x)\ \mathrm{si}\ x \geq 0 \\ 0\ \mathrm{sinon} \end{matrix}\right.
  • \mathbb{E}(X) = \frac{1}{\lambda}
  • V(X) = \frac{1}{\lambda^2}

Loi logistique

Article détaillé : Loi logistique.
  • f_X (x) = \frac{e^{-\frac{x-\mu}{s}}}{s\left(1+e^{-\frac{x-\mu}{s}}\right)^2}
  • \mathbb{E}(X) = \mu\,
  • V(X) = \frac{s^2\pi^2}{3}

Loi de Cauchy

Article détaillé : Loi de Cauchy.

f_X(x)=\frac{1}{\pi}\frac{1}{1+x^2}\,

La loi de Cauchy n'admet aucun moment (donc ni moyenne ni variance, entre autres).

Loi de Tukey-Lambda

La Loi de Tukey-Lambda est connue de façon implicite par la distribution de ses quantiles :

G(p) = {p^\lambda - (1-p)^\lambda\over \lambda}

elle a par la suite été généralisée.

Définition mathématique

En théorie des probabilités, une loi (ou mesure) de probabilité est une mesure positive \scriptstyle\ \mathbb{P}\ sur un espace mesurable \scriptstyle\ (\Omega, \mathcal A)\ , telle que \scriptstyle\ \mathbb{P}(\Omega) = 1. Le triplet \scriptstyle\ (\Omega, \mathcal A,\, \mathbb{P})\ est appelé espace probabilisé.

Définition — Soit une variable aléatoire réelle sur l'espace probabilisé \scriptstyle\ (\Omega, \mathcal A,\, \mathbb{P}), c'est-à-dire une fonction mesurable \scriptstyle\ X : \Omega \to \mathbb{R} (l'ensemble \scriptstyle\ \R étant muni de sa tribu borélienne \scriptstyle\ \mathcal B_\R). On appelle loi (de probabilité) de la variable aléatoire \scriptstyle\ X\ la mesure de probabilité \ \scriptstyle\mathbb{P}_X\ définie sur l'espace mesurable \ \scriptstyle(\R,\, \mathcal B_\R) par :

\mathbb{P}_X(B) = \mathbb{P}\left(X^{-1}(B)\right) = \mathbb{P}\left(X\in B\right),

pour tout borélien \ \scriptstyle B\ de \ \scriptstyle\R.\ Autrement dit, \ \scriptstyle\mathbb{P}_X\ est la mesure image de \scriptstyle\ \mathbb{P}\ par \scriptstyle\ X\ .

Deux variables aléatoires réelles \scriptstyle\ X\ et \scriptstyle\ Y\ ont même loi si \ \scriptstyle\mathbb{P}_X\ =\ \scriptstyle\mathbb{P}_Y\ (égalité de fonctions). Cela se réécrit

\forall B\in\mathcal B_\R,\qquad\mathbb{P}_X(B)\ = \mathbb{P}_Y(B),

ou bien encore

\forall B\in\mathcal B_\R,\qquad\mathbb{P}(X\in B)\ = \mathbb{P}(Y\in B).

Plus généralement, deux variables aléatoires réelles \scriptstyle\ X\ et \scriptstyle\ Y\ ont même loi si

\mathbb{E}\left[\phi(X)\right]\ = \mathbb{E}\left[\phi(Y)\right]

pour toute fonction \scriptstyle\ \phi\ de \scriptstyle\ \R\ dans \scriptstyle\ \R\ telle qu'au moins un des deux termes de l'égalité ait un sens. Cela est dû au théorème de transfert, d'après lequel

Théorème de transfert — Soit une variable aléatoire réelle \scriptstyle\ X : \Omega \to\R.\ Alors,

\mathbb{E}\left[\phi(X)\right] = \int_\R~\phi(x)~\mathbb{P}_X(dx),

pour toute fonction \scriptstyle\ \phi\ de \scriptstyle\ \R\ dans \scriptstyle\ \R\ telle qu'au moins un des deux termes de l'égalité ait un sens.

L'intégrale apparaissant dans le deuxième terme est l'intégrale, au sens de la théorie de la mesure, de la fonction φ par rapport à la mesure \ \scriptstyle\mathbb{P}_X.\ Cette intégrale prend la forme d'une somme ou d'une intégrale dans les deux cas classiques où X est discrète et où X est à densité, voir ci-dessous.

Caractérisation de la loi de probabilité d'une variable aléatoire réelle

En probabilité, il est crucial de pouvoir vérifier que deux variables aléatoires (réelles ou pas) ont la même loi de manière la plus économique possible, or les caractérisations ci-dessus exigent de vérifier des familles d'identités beaucoup trop riches (pour tout borélien B, pour toute fonction borélienne φ ...). Une solution plus ergonomique est fournie par les notions de fonction de répartition, ou de fonction caractéristique.

Caractérisation à l'aide de la fonction de répartition

La loi d'une variable aléatoire réelle est caractérisée par sa fonction de répartition : deux variables aléatoires réelles \scriptstyle\ X\ et \scriptstyle\ Y\ ont même loi si elles ont même fonctions de répartition, i.e. si

\forall x\in\mathbb{R},\qquad\mathbb{P}(X\le x)\ = \mathbb{P}(Y\le x).

Ainsi il suffit de vérifier l'égalité caractéristique pour une famille réduite de boréliens \scriptstyle\ B\ très particuliers, les boréliens de la forme \scriptstyle\ ]-\infty,x],\ pour démontrer les égalités \scriptstyle\ \mathbb{P}(X\in B)\ =\ \mathbb{P}(Y\in B) et \scriptstyle\ \mathbb{E}\left[\phi(X)\right]\ =\ \mathbb{E}\left[\phi(Y)\right] en toute généralité. Ce résultat crucial est une conséquence du Lemme de classe monotone dû à Wacław Sierpiński.

Caractérisation à l'aide de la fonction caractéristique

La loi d'une variable aléatoire réelle est caractérisée par sa fonction caractéristique : deux variables aléatoires réelles \scriptstyle\ X\ et \scriptstyle\ Y\ ont même loi si elles ont même fonction caractéristique, i.e. si

\forall t\in\mathbb{R},\qquad\mathbb{E}\left[e^{itX}\right]\ = \mathbb{E}\left[e^{itY}\right].

Ainsi il suffit de vérifier l'égalité caractéristique pour une famille réduite de fonctions \scriptstyle\ \phi\ très particulières, les fonctions de la forme \scriptstyle\ x\rightarrow\cos(tx)\ et \scriptstyle\ x\rightarrow\sin(tx),\ pour démontrer que \scriptstyle\ X\ et \scriptstyle\ Y\ ont même loi.

Caractérisation à l'aide de la transformée de Laplace

La loi d'une variable aléatoire réelle positive ou nulle est caractérisée par sa transformée de Laplace : deux variables aléatoires réelles positives ou nulles \scriptstyle\ X\ et \scriptstyle\ Y\ ont même loi si elles ont même transformée de Laplace, i.e. si

\forall \lambda>0,\qquad\mathbb{E}\left[e^{-\lambda X}\right]\ = \mathbb{E}\left[e^{-\lambda Y}\right].

Caractérisation à l'aide de la fonction génératrice

La loi d'une variable aléatoire à valeurs entières positives ou nulles est caractérisée par sa fonction génératrice : deux variables aléatoires à valeurs entières positives ou nulles \scriptstyle\ X\ et \scriptstyle\ Y\ ont même loi si elles ont même fonction génératrice, i.e. si

\forall s\in\mathbb{R},\qquad\mathbb{E}\left[s^{X}\right]\ = \mathbb{E}\left[s^{Y}\right].

Classification des lois de probabilité sur la droite réelle

Les lois énumérées dans cet article sont des mesures de probabilités sur \scriptstyle\ \mathbb{R}. Ces lois apparaissent en général dans les applications comme les lois de probabilité de certaines variables aléatoires réelles. Les lois énumérées dans cet article sont de deux types :

  • lorsque la loi de la variable aléatoire X est portée par un ensemble S
\text{— i.e.}\ \mathbb{P}\left(X\notin S\right)=0\text{ —}
tel que S est fini ou dénombrable, on parle de loi de probabilité discrète.
D'un point de vue pratique, les calculs de probabilités ou bien d'espérances liées à \scriptstyle\ X\ font alors intervenir des calculs de sommes finies ou de séries:
\mathbb{P}\left(X\in A\right)=\sum_{x\in A\cap S}\ \mathbb{P}\left(X=x\right),\qquad\mathbb{E}\left[\phi(X)\right]=\sum_{x\in S}\ \phi(x)\mathbb{P}\left(X=x\right).
Pour une variable discrète, on peut choisir comme ensemble \scriptstyle\ S\ l'ensemble des réels \scriptstyle\ a\ tels que \scriptstyle\ \mathbb{P}\left(X=a\right)>0.\
La deuxième égalité ci-dessus est la spécialisation du théorème de transfert au cas particulier des variables discrètes, puisque dans ce cas particulier, on a
\int_{\mathbb{R}}\ \phi(x)\ \mathbb{P}_X(dx)=\sum_{x\in S}\ \phi(x)\mathbb{P}\left(X=x\right).
  • lorsque la loi de \scriptstyle\ X\ est absolument continue par rapport à la mesure de Lebesgue sur \ \scriptstyle\mathbb{R}\ , ou bien, d'une manière équivalente, lorsque la fonction de répartition de \scriptstyle\ X\ est localement absolument continue, on parle de variable ou de loi absolument continue, ou bien de variable ou de loi à densité. Dans ce cas, en vertu du Théorème de Radon-Nikodym, la mesure \scriptstyle\ \mathbb{P}_X\ (ou la variable \scriptstyle\ X\ ) possède une densité de probabilité (notons-la \scriptstyle\ f_X\ ) par rapport à la mesure de Lebesgue. D'un point de vue pratique, les calculs de probabilités ou bien d'espérances liées à \scriptstyle\ X\ font alors intervenir des calculs d'intégrales :
\mathbb{P}\left(X\in A\right)=\int_{A}\ f_X(x)\,dx,\qquad\mathbb{E}\left[\phi(X)\right]=\int_{\mathbb{R}}\ \phi(x)\ f_X(x)\,dx.
Là encore, la deuxième égalité ci-dessus est la spécialisation du théorème de transfert, mais cette fois, au cas particulier des variables à densité, puisque dans ce cas particulier, on a
\int_{\mathbb{R}}\ \phi(x)\ \mathbb{P}_X(dx)=\int_{\mathbb{R}}\ \phi(x)\ f_X(x)\,dx.
Une variable à densité \scriptstyle\ X\ vérifie \scriptstyle\ \mathbb{P}\left(X=a\right)=0\ pour tout nombre réel \scriptstyle\ a.\ Toutefois, cette dernière propriété, qui oppose les variables à densité aux variables discrètes, n'est pas caractéristique des variables à densité.

Il existe d'autres types de variables aléatoires réelles :

  • la loi d'une variable aléatoire \scriptstyle\ X\ peut très bien n'être ni discrète ni absolument continue. Elle peut, par exemple, être un mélange des deux : si la loi de la durée de vie (avant panne) \scriptstyle\ Y\ d'un composant d'un certain type suit la loi exponentielle d'espérance 1 (an), et si par mesure de sécurité, on décide de remplacer chaque composant en cas de panne, mais aussi dès que le composant atteint l'age d'un an, même s'il n'est pas encore tombé en panne, alors la durée d'utilisation \scriptstyle\ X\ du composant (\scriptstyle\ X=1\wedge Y\ ) n'est ni discrète ni absolument continue. En effet les calculs de probabilités ou bien d'espérances liées à \scriptstyle\ X\ font alors intervenir des calculs d'intégrales et de sommes :
\mathbb{P}\left(X\in A\right)=e^{-1}1_A(1)+\int_{A}\ e^{-x}\,1_{[0,1]}(x)\,dx,\qquad\mathbb{E}\left[\phi(X)\right]=e^{-1}\phi(1)+\int_{0}^1\ \phi(x)\ e^{-x}\,dx.
  • dans le cas précédent, la fonction de répartition de la durée d'utilisation \scriptstyle\ X\ est discontinue en 1. C'est une propriété générale : la fonction de répartition d'une variable aléatoire réelle \scriptstyle\ X\ est discontinue en \scriptstyle\ x\ si et seulement si \scriptstyle\ \mathbb{P}\left(X=x\right)>0.\ On voit que les variables à densité ont des fonctions de répartitions localement absolument continues, donc, a fortiori, continues sur \scriptstyle\ \mathbb{R},\ alors que les fonctions de répartition des variables discrètes et du mélange évoqué précédemment possèdent des discontinuités sur la droite réelle. Le tableau est encore compliqué par l'existence de variables aléatoires dont la fonction de répartition est continue sur \scriptstyle\ \mathbb{R},\ mais pas absolument continue, et qui ne sont donc pas à densité. C'est le cas, par exemple, de
X\ =\ \sum_{n\ge 1}\ 2\,Y_n\,3^{-n},
où les \scriptstyle\ Y_n\ désignent une suite de variables de Bernoulli indépendantes de paramètre 0,5. \scriptstyle\ X\ est un nombre dont on tire le développement triadique à pile ou face : à chaque pile on ajoute le chiffre 2, et à chaque face le chiffre 0, excluant ainsi le chiffre 1. La fonction de répartition de \scriptstyle\ X\ est l'escalier de Cantor. Une telle variable doit-elle être appelée continue (sa fonction de répartition l'est), ou pas (elle n'a pas de densité de probabilité) ? Le débat n'est pas très aigu, car ce type de variables apparait rarement dans les applications.

Histoire

L'allure générale des lois de probabilité usuelles fut au début observée empiriquement, puis on en formalisa la définition dans le cadre de la théorie des probabilités en mathématiques.

Maximum d'entropie

Les lois de probabilité usuelles sont souvent classées par familles dépendant d'un paramètre. La loi normale par exemple est paramétrée par sa moyenne et son écart type. La plupart des familles usuelles de lois de probabilités sont celles offrant le maximum d'entropie (l'entropie est une mesure de l'information moyenne d'une source, au sens de Claude Shannon, donc le plus d'information) sous contraintes, par exemple :

  • La distribution uniforme est celle d'entropie maximale parmi les lois à support borné.
  • La distribution normale est celle d'entropie maximale parmi toutes les lois possibles ayant même moyenne et même écart type.
  • La distribution exponentielle est celle d'entropie maximale parmi les lois portées par \ \scriptstyle\mathbb{R}_+\ et ayant la même moyenne.
  • Les lois scalantes comme celle de Zipf ou de Mandelbrot sont d'entropie maximale parmi celles auxquelles on impose la valeur du logarithme d'une moyenne, c'est-à-dire un ordre de grandeur.

En quelque sorte, ces lois ne contiennent pas plus d'information que ce qui est obligatoire. Ce sont les moins prévenues de toutes les lois compatibles avec les observations ou les contraintes, et donc les seules admissibles objectivement comme distributions de probabilités a priori lorsque ces valeurs sont imposées et seules connues. Cette propriété joue un grand rôle dans les méthodes bayésiennes.

Voir aussi

Exemples de distribution


Références

  1. ↑ B.S. Everitt. 2006. The Cambridge Dictionary of Statistics, Third Edition. pp. 313–314. Cambridge University Press, Cambridge. ISBN 0-521-69027-7

Liens connexes

  • Portail des probabilités et des statistiques Portail des probabilités et des statistiques
v · Probabilités et statistiques
Théorie des probabilités Axiomes des probabilités • Espace probabilisable • Probabilité • Événement • Tribu • Indépendance
Probabilités élémentaires Moyenne • Espérance • Médiane • Variance • Écart type
Loi de probabilité Variable aléatoire • Loi de Bernoulli • Loi de Poisson • Loi uniforme • Loi normale • Loi de Student • Loi de Fisher • Variables iid
Convergence de lois Théorème central limite • Loi des grands nombres • Théorème de Borel-Cantelli
Calcul stochastique Marche aléatoire • Chaîne de Markov • Processus stochastique • Processus de Markov • Martingale • Mouvement brownien • Équation différentielle stochastique
Statistiques
Statistique descriptive Échantillon • Quantile • Intervalle de confiance • Représentations de données • Histogramme • Diagramme circulaire • Boîte à moustaches • Régression linéaire • Méthode des moindres carrés
Statistique mathématique Fonction de répartition empirique • Théorème de Glivenko-Cantelli • Inférence bayésienne
Tests statistiques Test d'hypothèse • Hypothèse statistique • Estimateur • Test du χ² • Test t • Test de Fisher
Applications Économétrie • Mécanique statistique • Jeu de hasard • Biomathématique • Mathématiques financières

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Loi de probabilité de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Loi De Probabilité — Une loi de probabilité ou distribution de probabilité a commencé par décrire les répartitions typiques des fréquences d apparition des résultats d un phénomène aléatoire. Dans le dernier quart du XXe siècle, on a largement étendu le concept… …   Wikipédia en Français

  • Loi de probabilite — Loi de probabilité Une loi de probabilité ou distribution de probabilité a commencé par décrire les répartitions typiques des fréquences d apparition des résultats d un phénomène aléatoire. Dans le dernier quart du XXe siècle, on a largement …   Wikipédia en Français

  • Loi logarithmique (probabilité) — Logarithmique Paramètres Support Densité de probabilité (fonction de masse) Fonction …   Wikipédia en Français

  • Loi De Probabilité À Plusieurs Variables — Dans certains problèmes interviennent simultanément plusieurs variables aléatoires. Mis à part les cas particuliers de variables indépendantes (notion définie ci dessous) et de variables liées fonctionnellement, cela introduit la notion de loi de …   Wikipédia en Français

  • Loi de probabilite a plusieurs variables — Loi de probabilité à plusieurs variables Dans certains problèmes interviennent simultanément plusieurs variables aléatoires. Mis à part les cas particuliers de variables indépendantes (notion définie ci dessous) et de variables liées… …   Wikipédia en Français

  • Loi de probabilité à plusieurs variables — Dans certains problèmes interviennent simultanément plusieurs variables aléatoires. Mis à part les cas particuliers de variables indépendantes (notion définie ci dessous) et de variables liées fonctionnellement, cela introduit la notion de loi de …   Wikipédia en Français

  • Probabilite — Probabilité La probabilité (du latin probabilitas) est une évaluation du caractère probable d un évènement. En mathématiques, l étude des probabilités est un sujet de grande importance donnant lieu à de nombreuses applications. La probabilité d… …   Wikipédia en Français

  • Probabilité et statistique — Probabilité La probabilité (du latin probabilitas) est une évaluation du caractère probable d un évènement. En mathématiques, l étude des probabilités est un sujet de grande importance donnant lieu à de nombreuses applications. La probabilité d… …   Wikipédia en Français

  • Loi Normale — Distribution gaussienne Densité de probabilité / Fonction de masse La courbe rouge représente la fonction φ (voir texte), densité de probabilité d une variable suivant une loi normale centrée réduite Fonction de répartition …   Wikipédia en Français

  • Loi Normale Reduite — Loi normale Distribution gaussienne Densité de probabilité / Fonction de masse La courbe rouge représente la fonction φ (voir texte), densité de probabilité d une variable suivant une loi normale centrée réduite Fonction de répartition …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”