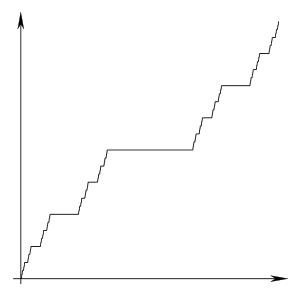
Escalier De Cantor

Escalier De Cantor

Escalier de Cantor

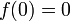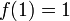L'escalier de Cantor, ou l'escalier du diable, est le graphe d'une fonction continue f\, sur [0,1]\,, telle que f(0)=0\,, f(1)=1\,, qui est dérivable presque partout, la dérivée étant presque partout nulle.

Sommaire

Quelques rappels d'analyse élémentaire

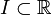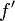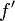Soit f\, une fonction continue sur un intervalle I\subset\mathbb{R}, de dérivée f^\prime. Si f^\prime s'annule sur I\,, alors f\, est constante. C'est une conséquence immédiate du théorème des accroissements finis.

L'escalier de Cantor montre que la conclusion est fausse si on suppose seulement que 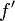f^\prime s'annule presque partout.

On dispose cependant des résultats suivants :

Construction

Escalier de Cantor

On suit pas à pas la construction de l'ensemble de Cantor K_3\,

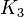
On prend 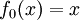f_0(x)=x\,. La fonction 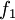f_1\, est la fonction continue affine par morceaux qui vaut 0 en 0, 1 en 1, et \frac{1}{2}\, sur [1/3,2/3]\,

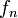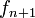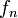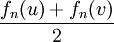On passe de même de f_n\, à f_{n+1}\, en remplaçant, f_n\,, sur chaque intervalle [u,v]\, où elle n'est pas constante, par la fonction linéaire par morceaux qui vaut \frac{f_n(u)+f_n(v)}{2} sur [\frac{2u}{3}+\frac{v}{3},\frac{2v}{3}+\frac{u}{3}]

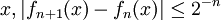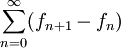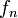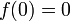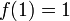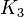Alors on vérifie que pour tout x,\vert f_{n+1}(x)-f_n(x)\vert\le 2^{-n}, ce qui montre que la série de fonctions \sum_{n=0}^\infty (f_{n+1}-f_n) converge uniformément, et donc que la suite f_n\, converge uniformément. La fonction limite f\, est continue, monotone, et l'on a f(0)=0\, , f(1)=1 \, comme annoncé. De plus, f\, a une dérivée nulle sur le complémentaire de l'ensemble de Cantor K_3\,, puisque ce complémentaire est une réunion d'intervalles sur lesquels f\,, par construction, est constante (d'où le nom d'escalier !)

Que nous apprend cet exemple ?

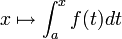  • Il est vrai (mais non trivial), que si f\, est une fonction mesurable bornée sur \mathbb{R}, la fonction x\mapsto \int_a^x f(t)dt est presque partout dérivable et de dérivée f(x). Mais il est faux que toute fonction presque partout dérivable soit égale à l'intégrale de sa dérivée, même si cette dernière est intégrable. C'est ce que nous enseigne l'escalier de Cantor. Pour avoir des résultats safisfaisant sur cette question, il faut introduire la notion de continuité absolue.
  • L'escalier de Cantor est la fonction de répartition d'une variable aléatoire réelle continue qui n'est pas à densité, et qui est même étrangère à la mesure de Lebesgue. En cela aussi, c'est un (contr)exemple très intéressant. On peut exhiber simplement une variable aléatoire réelle X prise au hasard entre 0 et 1 dont la fonction de répartition est l'escalier de Cantor : il suffit de tirer au hasard les chiffres successifs (0, 1 ou 2) du développement en base trois de X de manière un peu spéciale, à savoir par des tirages indépendants équiprobables restreints à 0 ou 2, le chiffre 1 étant exclus.

Voir aussi

Liens internes

Lien externe

L'escalier du diable

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Escalier de Cantor ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Escalier De Cantor de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

  • Escalier de cantor — L escalier de Cantor, ou l escalier du diable, est le graphe d une fonction continue sur , telle que , , qui est dérivable presque partout, la dérivée étant presque partout nulle. Sommaire …   Wikipédia en Français

  • Escalier de Cantor — L escalier de Cantor, ou l escalier du diable, est le graphe d une fonction continue sur , telle que , , qui est dérivable presque partout, la dérivée étant presque partout nulle. Sommaire 1 …   Wikipédia en Français

  • Cantor — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom.  Pour l’article homophone, voir Kantor (homonymie). Sur les autres projets Wikimedia : « Cant …   Wikipédia en Français

  • Ensemble de Cantor — En mathématiques, l ensemble de Cantor (ou ensemble triadique de Cantor, ou poussière de Cantor) est un sous ensemble remarquable de la droite réelle construit par le mathématicien allemand Georg Cantor[1]. Il s agit d un sous ensemble fermé de l …   Wikipédia en Français

  • Ensemble De Cantor — En mathématiques, l ensemble de Cantor (ou ensemble triadique de Cantor, ou poussière de Cantor) est un sous ensemble remarquable de la droite réelle construit par le mathématicien allemand Georg Cantor. Il s agit d un ensemble fermé du segment… …   Wikipédia en Français

  • Ensemble de cantor — En mathématiques, l ensemble de Cantor (ou ensemble triadique de Cantor, ou poussière de Cantor) est un sous ensemble remarquable de la droite réelle construit par le mathématicien allemand Georg Cantor. Il s agit d un ensemble fermé du segment… …   Wikipédia en Français

  • Ensemble triadique de Cantor — Ensemble de Cantor En mathématiques, l ensemble de Cantor (ou ensemble triadique de Cantor, ou poussière de Cantor) est un sous ensemble remarquable de la droite réelle construit par le mathématicien allemand Georg Cantor. Il s agit d un ensemble …   Wikipédia en Français

  • Poussière de Cantor — Ensemble de Cantor En mathématiques, l ensemble de Cantor (ou ensemble triadique de Cantor, ou poussière de Cantor) est un sous ensemble remarquable de la droite réelle construit par le mathématicien allemand Georg Cantor. Il s agit d un ensemble …   Wikipédia en Français

  • Fonction de répartition — Fonctions de répartition d une variable discrète, d une variable diffuse et d une variable avec atome, mais non discrète. En théorie des probabilités ou en statistiques, la fonction de répartition d une variable aléatoire réelle caractérise la… …   Wikipédia en Français

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”