Grand dodecaedre etoile tronque
- Grand dodecaedre etoile tronque
-
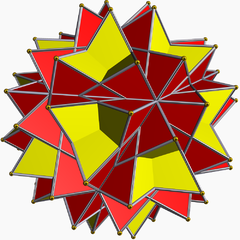
Grand dodécaèdre étoilé tronqué
En géométrie, le grand dodécaèdre étoilé tronqué est un polyèdre uniforme non-convexe, indexé sous le nom U66.
Il partage ses sommets avec le petit icosicosidodécaèdre.
Coordonnées cartésiennes
Les coordonnées cartésiennes pour les sommets d'un grand dodécaèdre étoilé tronqué sont toutes les permutations paires de
- (0, ±τ, ±(2−1/τ))
- (±τ, ±1/τ, ±2/τ)
- (±1/τ2, ±1/τ, ±2)
où τ = (1+√5)/2 est le nombre d'or (quelquefois écrit φ).
Voir aussi
Liste des polyèdres uniformes
Lien externe
 Portail de la géométrie
Portail de la géométrie
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Grand dodecaedre etoile tronque de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Grand Dodécaèdre Étoilé Tronqué — Type Polyèdre uniforme Éléments F=32, A=90, S=60 (χ=2) Faces par cotés 20{3}+12{10 … Wikipédia en Français
Grand dodécaèdre étoilé tronqué — Type Polyèdre uniforme Éléments F=32, A=90, S=60 (χ=2) Faces par côtés 20{3}+12{10/3} … Wikipédia en Français
Grand Dodécaèdre Étoilé — Type Solide de Kepler Poinsot Faces Triangle Éléments : · Faces · Arêtes · Sommets · Caractéristique 12 30 20 2 Faces par sommet … Wikipédia en Français
Grand dodecaedre etoile — Grand dodécaèdre étoilé Grand dodécaèdre étoilé Type Solide de Kepler Poinsot Faces Triangle Éléments : · Faces · Arêtes · Sommets · Caractéristique 12 30 20 2 Faces par sommet … Wikipédia en Français
Grand dodécaèdre étoilé — Ne pas confondre avec les autres dodécaèdres. Grand dodécaèdre étoilé … Wikipédia en Français
Petit dodecaedre etoile tronque — Petit dodécaèdre étoilé tronqué Petit dodécaèdre étoilé tronqué Type Polyèdre uniforme Éléments F=24, A=90, S=60 (χ= 6) Faces par cotés 12{5}+12{10 … Wikipédia en Français
Petit dodécaèdre étoilé tronqué — Type Polyèdre uniforme Éléments F=24, A=90, S=60 (χ= 6) Faces par côtés 12{5}+12{10/3} … Wikipédia en Français
Grand Dodécaèdre — Type Solide de Kepler Poinsot Faces Triangle Éléments : · Faces · Arêtes · Sommets · Caractéristique 12 30 12 6 Faces par sommet 12{5} … Wikipédia en Français
Grand dodecaedre — Grand dodécaèdre Grand dodécaèdre Type Solide de Kepler Poinsot Faces Triangle Éléments : · Faces · Arêtes · Sommets · Caractéristique 12 30 12 6 Faces par sommet 12{5} … Wikipédia en Français
Grand Dodécaèdre Tronqué — Type Polyèdre uniforme Éléments F=24, A=90, S=60 (χ= 6) Faces par cotés 12{5/2}+12{10} … Wikipédia en Français