- Grand dodecaedre
-
Grand dodécaèdre
Grand dodécaèdre 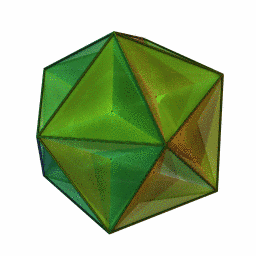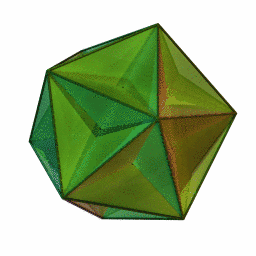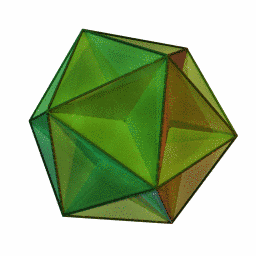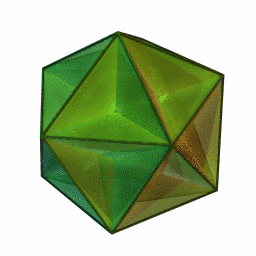
Type Solide de Kepler-Poinsot Faces Triangle Éléments :
· Faces
· Arêtes
· Sommets
· Caractéristique
12
30
12
6Faces par sommet 12{5} Sommets par face Isométries Dual Petit dodécaèdre étoilé Propriétés régulier et non-convexe En géométrie, le grand dodécaèdre est un solide de Kepler-Poinsot. C'est un des quatre polyèdres réguliers non-convexes. Il est composé de 12 faces pentagonales, avec cinq pentagones se rencontrant à chaque sommet, se coupant les uns les autres en créant un trajet pentagrammique.
Les 12 sommets et les 30 arêtes sont partagées avec l'icosaèdre.
Cette forme a été à la base du puzzle de type Rubik's Cube nommé l'étoile d'Alexandre.
En enlevant les parties concaves, nous obtenons un dodécaèdre.
Il est considéré comme la deuxième des trois stellations du dodécaèdre.
Si le grand dodécaèdre est considéré comme une surface géométrique proprement intersectée, il possède la même topologie qu'un triaki-icosaèdre à pyramides concaves plutôt qu'à pyramides convexes.
Comme une stellation
Il peut aussi être construit comme la deuxième des quatre stellations du dodécaèdre, et référencé comme le modèle de Wenninger [W21].
Liens externes
Solides géométriques Les polyèdres Les solides de Platon Tétraèdre - Cube - Octaèdre - Icosaèdre - Dodécaèdre Les solides d'Archimède Tétraèdre tronqué - Cube tronqué - Octaèdre tronqué - Dodécaèdre tronqué - Icosaèdre tronqué - Cuboctaèdre - Cube adouci - Icosidodécaèdre - Dodécaèdre adouci - Petit rhombicuboctaèdre - Grand rhombicuboctaèdre - Petit rhombicosidodécaèdre - Grand rhombicosidodécaèdre Les solides de Kepler-Poinsot Petit dodécaèdre étoilé - Grand dodécaèdre étoilé - Grand dodécaèdre - Grand icosaèdre Les solides de Catalan Triakioctaèdre - Tétrakihexaèdre - Triakitétraèdre - Pentakidodécaèdre - Triaki-icosaèdre - Dodécaèdre rhombique - Icositétraèdre pentagonal - Triacontaèdre rhombique - Hexacontaèdre pentagonal - Icositétraèdre trapézoïdal - Hexakioctaèdre - Hexacontaèdre trapézoïdal - Hexaki icosaèdre Les solides de Johnson Les solides de révolution Boule - Cylindre de révolution - Cône de révolution - Tore - Paraboloïde de révolution - Portail de la géométrie
- Portail des mathématiques
Catégorie : Polyèdre
Wikimedia Foundation. 2010.
