- Grand dirhombicosidodecaedre
-
Grand dirhombicosidodécaèdre
Grand dirhombicosidodécaèdre 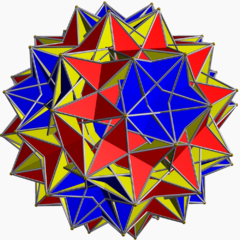
Type Polyèdre uniforme Éléments F=124, A=240, S=60 (χ=-56) Faces par cotés 40{3}+60{4}+24{5/2} Configuration de sommet (4.5/3.4.3.4.
5/2.4.3/2)/2Symbole de Wythoff |3/2 5/3 3 5/2 Groupe de symétrie Ih Références d'indexation U75, C92, W119 
(4.5/3.4.3.4.
5/2.4.3/2)/2
(Figure de sommet)Fichier:Wideblank.png
Grand dirhombicosadodécacron
(Polyèdre dual)En géométrie, le grand dirhombicosidodécaèdre est un polyèdre uniforme non-convexe, indexé sous le nom U75.
C'est le seul polyèdre uniforme avec plus de six faces se rencontrant à un sommet. Chaque sommet a 4 carrés qui passent à travers l'axe central du sommet (et ainsi à travers le centre de la figure), alternant avec deux triangles et deux pentagrammes.
C'est aussi le seul polyèdre uniforme qui ne peut pas être construit par la construction de Wythoff. Il a un symbole de Wythoff spécial | 3/2 5/3 3 5/2.
Il a été surnommé le "monstre de Miller" (d'après J.C.P. Miller, qui, avec H.S.M. Coxeter et M. S. Longuet-Higgins énuméra les polyèdres uniformes en 1954).
Si la définition d'un polyèdre uniforme est assouplie pour autoriser un nombre pair de faces adjacentes à une arête, alors ce polyèdre donne lieu à un autre polyèdre, le grand dirhombidodécaèdre disadouci qui a les mêmes sommets et arêtes mais avec un arrangement différent de faces triangulaires.
Les sommets et les arêtes sont aussi communs aux composés uniformes de 20 octaèdres ou tétrahémihexaèdres. Par ailleurs, 180 arêtes sont communes au grand dodécicosidodécaèdre adouci.
La forme est aussi significative mathématiquement. À la conférence mathématique de 1972 à Pasadena, le Dr. Steven McHarty, un professeur de mathématiques de Princeton a montré, en utilisant la théorie des nombres, que la conversion de Wythoff tient compte des grandeurs inverses de séries infinies. Ceci signifie qu'il existe plus de points le long d'une arête quelconque qui sont contenus dans la surface de la forme, et plus de points dans la surface qui sont contenus dans le volume de l'objet.
Coordonnées cartésiennes
Les coordonnées cartésiennes pour les sommets d'un grand dirhombicosidodécaèdre centré à l'origine sont toutes les permutations paires de
- (0, ±2/τ, ±2/√τ)
- (±(−1+1/√τ3), ±(1/τ2−1/√τ), ±(1/τ+√τ))
- (±(−1/τ+√τ), ±(−1−1/√τ3, ±(1/τ2+1/√τ))
où τ = (1+√5)/2 est le nombre d'or (quelquefois écrit φ). Ces sommets résultent d'une longueur d'arête de 2√2.
Voir aussi
Liens externes
- Portail de la géométrie
Catégorie : Polyèdre
Wikimedia Foundation. 2010.
