Théorème de Descartes-Euler

Le théorème de Descartes-Euler (ou relation d'Euler), formulé par Leonhard Euler en 1752, énonce une formule mathématique qui relie le nombre de côtés, de sommets, et de faces dans un polyèdre de genre 0 (c'est-à-dire, intuitivement, un polyèdre « sans trou ») ; tout polyèdre convexe est de genre 0.

Il semble cependant que Descartes^[1] ait prouvé une relation analogue dans un traité jamais publié. C'est la raison pour laquelle cette relation porte ce double nom.

Énoncé

Soit un polyèdre de genre 0, on note :

• f   le nombre de faces de celui-ci,
• a   le nombre d'arêtes de celui-ci,
• s   le nombre de sommets de celui-ci.

On peut démontrer qu'on a toujours :  

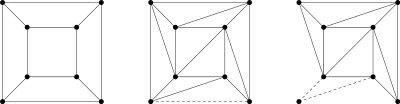
Exemples et contre-exemples

On peut procéder à la vérification de la propriété pour les cinq solides platoniciens :

Nom	Image	S (sommets)	A (arêtes)	F (faces)	Caractéristique d'Euler : S − A + F
Tétraèdre	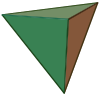	4	6	4	2
Hexaèdre ou cube	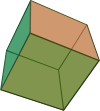	8	12	6	2
Octaèdre	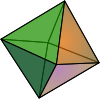	6	12	8	2
Dodécaèdre régulier	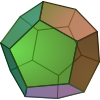	20	30	12	2
Icosaèdre		12	30	20	2

Si les polyèdres ne sont pas convexes, ils ne sont pas du genre 0 et on ne peut pas appliquer le théorème de Descartes-Euler. On peut alors trouver pour S − A + F des valeurs différentes de 2 :

Nom	Image	S (Sommets)	A (arêtes)	F (faces)	Caractéristique d'Euler : S − A + F
Tetrahemihexaèdre		6	12	7	1
Octahemioctaèdre	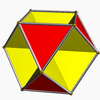	12	24	12	0
Cubohemioctaèdre	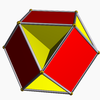	12	24	10	−2

Preuve

La preuve présentée ici est la première démonstration rigoureuse de la relation d'Euler. Elle a été donnée par Cauchy, alors âgé de 20 ans.

Soit un polyèdre de genre 0, on va chercher à démontrer que dans celui-ci. On enlève une face à notre polyèdre. En écartant vers l'extérieur les côtés de cette face manquante, on déforme le polyèdre en l'aplatissant et on obtient alors un graphe plan dont les nœuds sont les sommets et les arcs sont les arêtes déformées (cette déformation est appelée un homéomorphisme). Le nombre de sommets, d'arêtes et de faces n'a pas changé par rapport au polyèdre de départ (considérant que tout l'extérieur de notre graphe représente la face enlevée).

Premières étapes de la démonstration pour le cube

Maintenant, à chaque fois qu'on voit une face ayant plus de trois côtés, on trace une diagonale (c’est-à-dire un arc joignant deux sommets non directement reliés). Cette opération ajoute une face et une arête à notre graphe et ne modifie pas le nombre de sommets, donc l'expression reste inchangée. On répète cette opération jusqu'à ne plus avoir que des faces triangulaires.

Arrivé à ce stade, on répète les deux opérations suivantes :

1. On supprime un à un tous les triangles qui comportent un seul côté aux frontières extérieures de notre graphe. À chaque suppression, on enlève une arête et une face (pas de modification au niveau des sommets). Cela conserve donc l'expression .
2. On supprime un à un tous les triangles qui comportent deux arêtes aux frontières extérieures de notre graphe. À chaque suppression, on enlève un sommet, deux arêtes et une face. Cela conserve donc à nouveau l'expression .

En répétant les deux étapes précédentes, l'une après l'autre, il ne finit par rester qu'un seul triangle. Ce triangle seul compte deux faces (l'intérieur et l'extérieur du triangle), trois arêtes et trois sommets. Ainsi f = 2, a = 3, et s = 3, donc est égale à 2. Cette expression est égale à l'expression d'origine car chaque étape maintenait l'égalité de cette expression. On en conclut que notre polyèdre de départ vérifiait l'expression . La relation est donc prouvée.

Lien avec les pavages de la sphère

On peut ramener cette relation à une propriété de pavage de la sphère, en utilisant la technique imagée suivante

• placer une source de lumière au centre de gravité G du polyèdre
• considérer une sphère de centre G et de rayon suffisamment grand, et la considérer comme un écran sur lequel se projettent les ombres des arêtes du polyèdre.

Cette opération est en fait une projection centrale. On obtient alors sur la sphère des « sommets », images des sommets du polyèdre, des « arêtes » qui sont des arcs de grands cercles, et des portions de sphères délimitées par les arêtes qui sont des « polygones sphériques ». On peut qualifier cette configuration de pavage de la sphère par des polygones sphériques.

On montre encore que pour un tel pavage, la formule F + S - A = 2 est vérifiée. Une des méthodes possibles est d'utiliser des propriétés des triangles sphériques.

Applications

• Il est impossible de recouvrir une sphère seulement par des hexagones, même non réguliers, afin de former une géode, car un tel recouvrement ne respecterait pas la relation d'Euler. En effet, dans un polyèdre à faces uniquement hexagonales, chaque sommet est commun à 3 faces et chaque arête à 2 faces. Comme tout hexagone a 6 côtés et 6 sommets, un tel polyèdre doit donc comporter plus de sommets que de faces et plus d'arêtes que de faces. Donc, si f est le nombre de faces, le nombre d'arêtes a doit être égal à 3f et le nombre de sommets s à 2f. On a alors :

et la relation d'Euler n'est pas vérifiée.

Par contre, remplaçons certains hexagones de ce recouvrement impossible par des pentagones. Si le nombre de faces ne varie pas, le nombre d'arêtes et de sommets diminue : pour chaque pentagone ajouté, on a ( 6 - 5 )÷ 2 arêtes, c'est-à-dire une demi-arête en moins et (6 - 5)÷3 sommets, c'est-à-dire un tiers de sommet en moins;   s − a + f   augmente donc à chaque fois de la différence, c'est-à-dire d'un sixième. Pour que la relation d'Euler soit respectée, il faut que   s − a + f   initialement à 0, devienne égal à 2, donc augmente de 12÷6. Bref, il faut remplacer 12 hexagones par autant de pentagones. Le nombre des sommets s est alors de 2f - 4 et celui des arêtes a de 3f - 6. C'est ainsi que l'on rencontre l'icosaèdre tronqué (ballon de football ou fullerène C₆₀). Un cas extrême est celui du dodécaèdre régulier ( f = 12 ), où il ne reste plus aucun hexagone. Dans la figure ci-dessous (où f = 344 faces), quatre des douze pentagones sont visibles.

géode duale

La version de Descartes

Dans son mémoire inédit, Descartes énonce le théorème suivant :

« L'angle droit étant pris pour unité, la somme des angles de toutes les faces d'un polyèdre convexe est égale à quatre fois le nombre de sommets diminué de 2. »

L'aspect du théorème semble fort éloigné de la relation d'Euler. Elle lui est pourtant rigoureusement équivalente, et Descartes, dans les applications qu'il en fait, passe assez naturellement de cette forme à celle d'Euler.

Preuve de l'équivalence :

Il faut se servir de la propriété de la somme des angles d'un polygone convexe : si le polygone convexe a n côtés, la somme des angles vaut 2(n − 2) droits.

La somme de tous les angles sur toutes les faces est donc droits (en effet la somme des nombres de côtés de chaque face donne deux fois le nombre d'arêtes).

L'égalité de Descartes s'écrit donc

formule rigoureusement équivalente à

s − a + f = 2.

Généralisations

Henri Poincaré, en 1893^[2], a démontré que la relation d'Euler se généralisait à tout n-polytope convexe :

N₀ − N₁ + N₂ − N₃ + ... + ( − 1)^{n − 1}N_{n − 1} = 1 − ( − 1)ⁿ

où n est la dimension du polytope et N_k le nombre de k-simplexes du n-polytope (N₀ est le nombre de sommets, N₁ le nombre d'arêtes, N₂ le nombre de faces, etc.).

La quantité ., si elle vaut 2 dans le cas des polyèdres de genre 0, peut prendre d'autres valeurs suivant la nature du polyèdre et est appelée caractéristique d'Euler (ou d'Euler-Poincaré) du solide. Cette caractéristique est un nombre qu'on peut attacher naturellement aux surfaces. Elle est par exemple de 2 pour la sphère. Il s'agit d'un invariant topologique, c'est-à-dire que toutes les variétés homéomorphes à la sphère ont la même caractéristique. La convexité n'est finalement qu'une hypothèse particulière assurant qu'il existe bien un tel homéomorphisme.

Notes et références

Voir aussi

Articles connexes

• Relation d'Euler dans le triangle
• Caractéristique d'Euler

• Portail de la géométrie