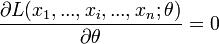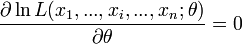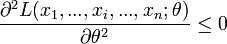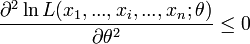Maximum De Vraisemblance

Maximum de vraisemblance

L'estimation du maximum de vraisemblance est une méthode statistique courante utilisée pour inférer les paramètres de la distribution de probabilité d'un échantillon donné.

Cette méthode a été développée par le statisticien et généticien Ronald Fisher entre 1912 et 1922.

L'estimateur du maximum de vraisemblance peut exister et être unique, ne pas être unique, ou ne pas exister.

Définitions

Soit $X$ une variable aléatoire, de loi quelconque, dont on veut estimer un paramètre $θ$ . On note 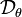$\mathcal{D}_\theta$ cette famille de lois paramétriques. Alors on définit une fonction $f$ telle que :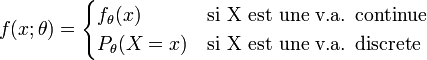 $f(x;\theta) = \begin{cases} f_\theta(x) & \text{si X est une v.a. continue} \\ P_\theta(X=x) & \text{si X est une v.a. discrete} \end{cases}$

$f θ (x)$ représente la densité de X (où $θ$ apparaît) et $P θ (X = x)$ représente une probabilité discrète (où $θ$ apparaît).

On appelle vraisemblance de $θ$ au vu des observations $(x 1,..., x i,..., x n)$ d'un n-échantillon indépendamment et identiquement distribué selon la loi 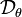$\mathcal{D}_\theta$ , le nombre :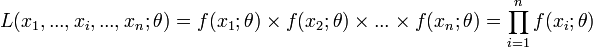

$L(x_1,...,x_i,...,x_n;\theta) = f(x_1;\theta) \times f(x_2;\theta) \times ...\times f(x_n;\theta) = \prod_{i=1}^n f(x_i;\theta)$

On cherche à trouver le maximum de cette vraisemblance pour que les probabilités des réalisations observées soient aussi maximum. Ceci est un problème d'optimisation. On utilise généralement le fait que si L est dérivable (ce qui n'est pas toujours le cas) et si L admet un maximum global en une valeur 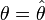$\theta = \hat \theta$ , alors la dérivée première s'annule en 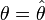$\theta = \hat \theta$ et que la dérivée seconde est négative. Réciproquement, si la dérivée première s'annule en 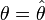$\theta = \hat \theta$ et que la dérivée seconde est négative en 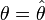$\theta = \hat \theta$ , alors 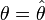$\theta = \hat \theta$ est un maximum local (et non global) de $L (x 1,..., x i,..., x n;θ)$ . Il est alors nécessaire de vérifier qu'il s'agit bien d'un maximum global. La vraisemblance étant positive et le logarithme népérien une fonction croissante, il est équivalent et souvent plus simple de maximiser le logarithme népérien de la vraissemblance (le produit se transforme en somme, ce qui est plus simple à dériver). On peut facilement construire la statistique $Y n = Θ$ qui est l'estimateur voulu.

Ainsi en pratique :

La condition nécessaire

$\frac{\partial L(x_1,...,x_i,...,x_n;\theta)}{\partial \theta} = 0$

$\frac{\partial \ln L(x_1,...,x_i,...,x_n;\theta)}{\partial \theta} = 0$

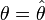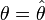permet de trouver la valeur $\theta = \hat \theta$ .

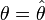$\theta = \hat \theta$ est un maximum local si la condition suffisante est remplie au point critique $\theta = \hat \theta$ :

$\frac{\partial^2 L(x_1,...,x_i,...,x_n;\theta)}{\partial \theta^2} \le 0$

$\frac{\partial^2 \ln L(x_1,...,x_i,...,x_n;\theta)}{\partial \theta^2} \le 0$

Pour simplifier, dans les cas de lois continues, où parfois la densité de probabilité est nulle sur un certain intervalle, on peut omettre d'écrire la vraisemblance pour cet intervalle uniquement.

Propriétés

L'estimateur obtenu par la méthode du maximum de vraisemblance est :

convergent, mais il peut être biaisé en échantillon fini.
asymptotiquement efficient, il atteint la borne de Cramer Rao.
asymptotiquement distribué selon une loi normale.

Exemples

Avec une loi discrète

On souhaite estimer le paramètre $λ$ d'une loi de Poisson à partir d'un n-échantillon.

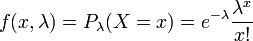
$f(x,\lambda) = P_\lambda(X=x) = e^{-\lambda} \frac{\lambda^x}{x!}$

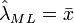L'estimateur du maximum de vraisemblance est : $\hat {\lambda}_{ML}= \bar x$

Démonstration

La vraisemblance s'écrit :

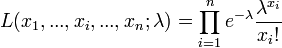
$L(x_1,...,x_i,...,x_n;\lambda) = \prod_{i=1}^n e^{-\lambda} \frac{\lambda^{x_i}}{x_i!}$

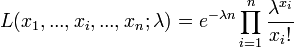
$L(x_1,...,x_i,...,x_n;\lambda) = e^{-\lambda n} \prod_{i=1}^n \frac{\lambda^{x_i}}{x_i!}$

La vraisemblance étant positive, on considère son Logarithme naturel :

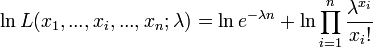
$\ln L(x_1,...,x_i,...,x_n;\lambda) = \ln e^{-\lambda n} + \ln \prod_{i=1}^n \frac{\lambda^{x_i}}{x_i!}$

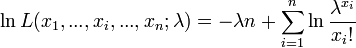
$\ln L(x_1,...,x_i,...,x_n;\lambda) = - \lambda n + \sum_{i=1}^n \ln \frac{\lambda^{x_i}}{x_i!}$

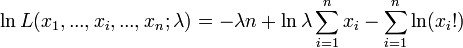
$\ln L(x_1,...,x_i,...,x_n;\lambda) = - \lambda n + \ln \lambda \sum_{i=1}^n x_i - \sum_{i=1}^n \ln (x_i!)$

La dérivée première s'annule quand :

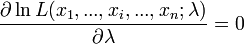
$\frac{\partial \ln L(x_1,...,x_i,...,x_n;\lambda)}{\partial \lambda} = 0$

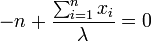
$-n + \frac{\sum_{i=1}^n x_i}{\lambda} = 0$

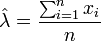
$\hat \lambda = \frac{\sum_{i=1}^n x_i}{n}$

La dérivée seconde s'écrit :

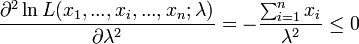
$\frac{\partial^2 \ln L(x_1,...,x_i,...,x_n;\lambda)}{\partial \lambda^2} = - \frac{\sum_{i=1}^n x_i}{\lambda^2} \le 0$

Ce ratio étant toujours négatif alors, l'estimation est donnée par :

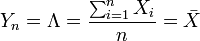
$Y_n = \Lambda = \frac{\sum_{i=1}^n X_i}{n} = \bar X$

Il est tout à fait normal de retrouver dans cet exemple didactique la moyenne empirique, car c'est le meilleur estimateur possible pour le paramètre $λ$ (qui représente aussi l'espérance d'une loi de Poisson).

Avec une loi continue

Loi exponentielle

On souhaite estimer le paramètre $α$ d'une loi exponentielle à partir d'un n-échantillon.

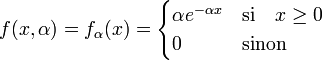
$f(x,\alpha) = f_\alpha(x) = \begin{cases} \alpha e^{-\alpha x} & \text{si} \quad x \ge 0 \\ 0 & \text{sinon} \end{cases}$

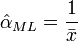L'estimateur du maximum de vraisemblance est : $\hat {\alpha}_{ML}= \frac{1}{\bar x}$

Démonstration

La vraisemblance s'écrit :

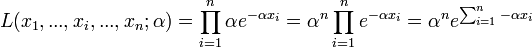
$L(x_1,...,x_i,...,x_n;\alpha) = \prod_{i=1}^n \alpha e^{-\alpha x_i} = \alpha^n \prod_{i=1}^n e^{-\alpha x_i} = \alpha^n e^{\sum_{i=1}^n -\alpha x_i}$

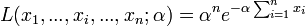
$L(x_1,...,x_i,...,x_n;\alpha) = \alpha^n e^{-\alpha \sum_{i=1}^n x_i}$

La vraisemblance étant positive, on considère son logarithme népérien:

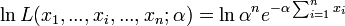
$\ln L(x_1,...,x_i,...,x_n;\alpha) = \ln \alpha^n e^{-\alpha \sum_{i=1}^n x_i}$

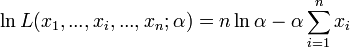
$\ln L(x_1,...,x_i,...,x_n;\alpha) = n \ln \alpha - \alpha \sum_{i=1}^n x_i$

La dérivée première s'annule quand :

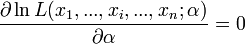
$\frac{\partial \ln L(x_1,...,x_i,...,x_n;\alpha)}{\partial \alpha} = 0$

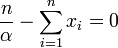
$\frac{n}{\alpha} - \sum_{i=1}^n x_i = 0$

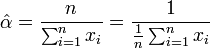
$\hat \alpha = \frac{n}{\sum_{i=1}^n x_i} = \frac{1}{\frac {1}{n} \sum_{i=1}^n x_i}$

La dérivée seconde s'écrit :

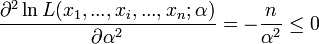
$\frac{\partial^2 \ln L(x_1,...,x_i,...,x_n;\alpha)}{\partial \alpha^2} = - \frac{n}{\alpha^2} \le 0$

Ce ratio est toujours négatif donc l'estimation est donnée par:

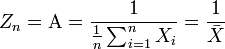
$Z_n = \Alpha = \frac{1}{\frac {1}{n} \sum_{i=1}^n X_i} = \frac{1}{\bar X}$

Là encore, il est tout à fait normal de retrouver l'inverse de la moyenne empirique, car on sait que l'espérance d'une loi exponentielle correspond à l'inverse du paramètre $α$ .

Loi normale

L'estimateur du maximum de vraisemblance de l'espérance $μ$ et la variance $σ 2$ d'une loi normale est:

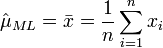
$\hat{\mu}_{ML} = \bar{x} = \frac{1}{n}\sum^{n}_{i=1}x_i$

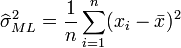$\widehat{\sigma}^2_{ML} = \frac{1}{n}\sum_{i=1}^n(x_i-\bar{x})^2$

Démonstration

Une loi normale

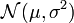$\mathcal{N}(\mu, \sigma^2)$ a la fonction de densité: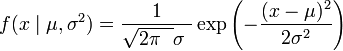

$f(x\mid \mu,\sigma^2) = \frac{1}{\sqrt{2\pi\ \ }\sigma\ } \exp{\left(-\frac {(x-\mu)^2}{2\sigma^2} \right)}$

la fonction de vraisemblance pour un échantillon de n valeurs indépendantes :

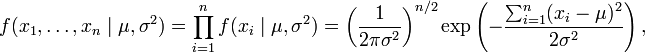
$f(x_1,\ldots,x_n \mid \mu,\sigma^2) = \prod_{i=1}^{n} f( x_{i}\mid \mu, \sigma^2) = \left( \frac{1}{2\pi\sigma^2} \right)^{n/2} \exp\left( -\frac{ \sum_{i=1}^{n}(x_i-\mu)^2}{2\sigma^2}\right),$

qui peut s'écrire plus simplement (voir Théorème de König-Huyghens):

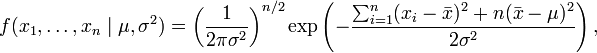
$f(x_1,\ldots,x_n \mid \mu,\sigma^2) = \left( \frac{1}{2\pi\sigma^2} \right)^{n/2} \exp\left(-\frac{ \sum_{i=1}^{n}(x_i-\bar{x})^2+n(\bar{x}-\mu)^2}{2\sigma^2}\right),$

où 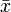$\bar{x}$ représente la moyenne de l'échantillon.

Nous avons là deux paramètres: $θ = μ,σ 2$ , donc il faut maximiser la fonction 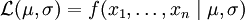$\mathcal{L} (\mu,\sigma) = f(x_1,\ldots,x_n \mid \mu, \sigma)$ selon les deux paramètres.

On va donc chercher la dérivée première et l'égaliser à zéro.

En l'occurrence, c'est la fonction de log-vraisemblance qui est maximisée ici.

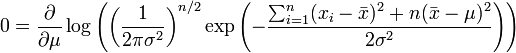
$0 = \frac{\partial}{\partial \mu} \log \left( \left( \frac{1}{2\pi\sigma^2} \right)^{n/2} \exp\left(-\frac{ \sum_{i=1}^{n}(x_i-\bar{x})^2+n(\bar{x}-\mu)^2}{2\sigma^2}\right) \right)$

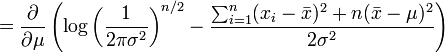
$= \frac{\partial}{\partial \mu} \left( \log\left( \frac{1}{2\pi\sigma^2} \right)^{n/2} - \frac{ \sum_{i=1}^{n}(x_i-\bar{x})^2+n(\bar{x}-\mu)^2}{2\sigma^2} \right)$

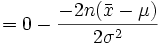
$= 0 - \frac{-2n(\bar{x}-\mu)}{2\sigma^2}$

et on obtient donc l'estimateur par le maximum de vraisemblance de l'espérance:

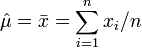
$\hat\mu = \bar{x} = \sum^{n}_{i=1}x_i/n$

On peut montrer en plus que cet estimateur sans biais:

$E \left[ \widehat\mu \right] = \mu$

Pour le second paramètre, σ, on cherche par analogie le maximum en fonction de σ.

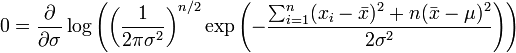
$0 = \frac{\partial}{\partial \sigma} \log \left( \left( \frac{1}{2\pi\sigma^2} \right)^{n/2} \exp\left(-\frac{ \sum_{i=1}^{n}(x_i-\bar{x})^2+n(\bar{x}-\mu)^2}{2\sigma^2}\right) \right)$

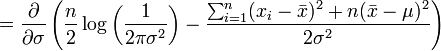
$= \frac{\partial}{\partial \sigma} \left( \frac{n}{2}\log\left( \frac{1}{2\pi\sigma^2} \right) - \frac{ \sum_{i=1}^{n}(x_i-\bar{x})^2+n(\bar{x}-\mu)^2}{2\sigma^2} \right)$

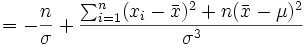
$= -\frac{n}{\sigma} + \frac{ \sum_{i=1}^{n}(x_i-\bar{x})^2+n(\bar{x}-\mu)^2}{\sigma^3}$

donc

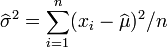
$\widehat\sigma^2 = \sum_{i=1}^n(x_i-\widehat{\mu})^2/n$

et on obtient finalement l'estimateur par le maximum de vraisemblance de la variance:

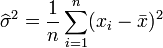
$\widehat\sigma^2 = \frac{1}{n} \sum_{i=1}^{n} (x_{i} - \bar{x})^2$

L'estimateur de la variance est par contre biaisé :

$E \left[ \widehat{\sigma^2} \right]= \frac{n-1}{n}\sigma^2$

L'estimateur de la variance est un bon exemple pour montrer que le maximum de vraisemblance peut fournir des estimateurs biaisés: un estimateur sans biais est donné en effet par: 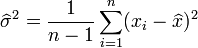$\widehat\sigma^2 = \frac{1}{n-1}\sum_{i=1}^n(x_i-\widehat{x})^2$ . Néanmoins, asymptotiquement, quand n tend vers l'infini, ce biais, qui est de 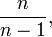$\frac{n}{n-1},$ tend vers 1 et l'estimateur est alors asymptotiquement sans biais.

Si la dérivée ne s'annule jamais

On souhaite estimer le paramètre a d'une loi uniforme à partir d'un n-échantillon.

$f(x,a) = f_a(x) = \begin{cases} \frac {1}{a} & \text{si} \quad x \in [0;a] \\ 0 & \text{sinon} \end{cases}$

La vraisemblance s'écrit :

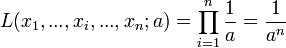
$L(x_1,...,x_i,...,x_n;a) = \prod_{i=1}^n \frac {1}{a} = \frac {1}{a^n}$

Intuitivement, il est clair que cette expression de la vraisemblance ne s'annule jamais (on peut la dériver pour s'en convaincre). Graphiquement dans le repère (a, L), sa représentation est une courbe décroissante de type "inverse" (convexe tournée vers l'origine).

La valeur de L sera maximum quand a sera très près de 0, donc quand a sera le plus petit possible (l'intervalle de la densité est alors réduit). Mais, pour que la densité soit vrai, le paramètre a doit être nécessairement plus grand que tous les $x i$ de l'échantillon.

On prend donc comme valeur qui maximise L, tout en vérifiant la définition de la loi de probabilité :

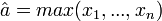
$\hat a = max(x_1,...,x_n)$

$W n = A = m a x (X 1,..., X n)$

Cet exemple permet de montrer, qu'un estimateur n'est pas toujours défini par une expression numérique explicite. Ainsi on sera amené parfois à considérer le maximum ou le minimum des échantillons.

Voir aussi

Le maximum a posteriori est une généralisation quand la distribution a priori n'est pas uniforme.
Information de Fisher
Fonction de vraisemblance

Portail des probabilités et des statistiques

Ce document provient de « Maximum de vraisemblance ».

Catégories : Optimisation | Estimation (statistique) | Algorithmique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Maximum De Vraisemblance de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Maximum de vraisemblance — L estimation du maximum de vraisemblance est une méthode statistique courante utilisée pour inférer les paramètres de la distribution de probabilité d un échantillon donné. Cette méthode a été développée par le statisticien et généticien Ronald… … Wikipédia en Français
méthode de maximum de vraisemblance — maksimaliojo tikėtinumo metodas statusas T sritis automatika atitikmenys: angl. maximum likelihood method vok. Methode der maksimalen Mutmaßlichkeit, f rus. метод максимального правдоподобия, m pranc. méthode de maximum de vraisemblance, f;… … Automatikos terminų žodynas
Maximum De Parcimonie — Les méthodes de Maximum de Parcimonie, ou plus simplement méthodes de parcimonie ou encore parcimonie de Wagner, sont une méthode statistique non paramétrique très utilisée, notamment pour l inférence phylogénétique. Cette méthode permet de… … Wikipédia en Français
Maximum de parcimonie — Les méthodes de Maximum de Parcimonie, ou plus simplement méthodes de parcimonie ou encore parcimonie de Wagner, sont une méthode statistique non paramétrique très utilisée, notamment pour l inférence phylogénétique. Cette méthode permet de… … Wikipédia en Français
Maximum a posteriori — L estimateur du maximum a posteriori ou à postériori (MAP), tout comme la méthode du maximum de vraisemblance, est une méthode pouvant être utilisée afin d estimer un certain nombre de paramètres inconnus, comme par exemple les parametres d une… … Wikipédia en Français
Vraisemblance — Sur les autres projets Wikimedia : « Vraisemblance », sur le Wiktionnaire (dictionnaire universel) Vraisemblance, en langage courant, est l attribut de ce qui semble intuitivement vrai, c est à dire, celui qu’on attribue à une… … Wikipédia en Français
maximum-likelihood method — maksimaliojo tikėtinumo metodas statusas T sritis automatika atitikmenys: angl. maximum likelihood method vok. Methode der maksimalen Mutmaßlichkeit, f rus. метод максимального правдоподобия, m pranc. méthode de maximum de vraisemblance, f;… … Automatikos terminų žodynas
Maximum de Parcimonie — Les méthodes de Maximum de Parcimonie, ou plus simplement méthodes de parcimonie ou encore parcimonie de Wagner, sont une méthode statistique non paramétrique très utilisée, notamment pour l inférence phylogénétique. Cette méthode permet de… … Wikipédia en Français
vraisemblance — [ vrɛsɑ̃blɑ̃s ] n. f. • 1358; de vrai et semblance, d apr. le lat. verisimilitudo ♦ Caractère vraisemblable; apparence de vérité. ⇒ crédibilité. L hypothèse « gagnait en force ce qu elle perdait en vraisemblance » (Proust ). « Soutenir avec… … Encyclopédie Universelle
Méthode de maximum de parcimonie — Maximum de Parcimonie Les méthodes de Maximum de Parcimonie, ou plus simplement méthodes de parcimonie ou encore parcimonie de Wagner, sont une méthode statistique non paramétrique très utilisée, notamment pour l inférence phylogénétique. Cette… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Maximum De Vraisemblance