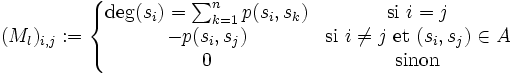Laplacienne
- Laplacienne
-
Matrice laplacienne
En théorie des graphes, une matrice laplacienne, ou matrice de Laplace, est une matrice représentant un graphe.
Définition
La matrice laplacienne d'un graphe G non-orienté et non-réflexif est définie par : Ml = Md − Ma où Md est la matrice des degrés de G et Ma la matrice d'adjacence de G.
Plus formellement, soit un graphe non-orienté et non-réflexif G=(S,A) de n sommets, pondéré par la fonction poids qui à tout arête (si,sj) associe son poids p(si,sj).
La matrice laplacienne de G vérifie :
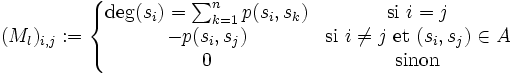
Applications
La matrice laplacienne est utilisée par le théorème de Kirchhoff pour calculer le nombre d' arbres couvrants d'un graphe.
La matrice laplacienne d'un graphe est utilisée dans le cadre du partitionnement de graphe par les méthodes spectrales.
Propriétés
La matrice laplacienne d'un graphe pondéré par des poids positifs est semi-définie positive.
|
Articles en rapport avec les matrices |
| Par forme |
|
| Transformée |
|
| En relation |
|
| Par propriété |
|
| Par famille |
|
| Particulière |
|
| Associée |
|
| Résultats |
|
| Voir aussi |
|
Catégories : Théorie algébrique des graphes | Matrice | Analyse numérique
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Laplacienne de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Matrice Laplacienne — En théorie des graphes, une matrice laplacienne, ou matrice de Laplace, est une matrice représentant un graphe. Définition La matrice laplacienne d un graphe G non orienté et non réflexif est définie par : Ml = Md − Ma où Md est la matrice… … Wikipédia en Français
Matrice laplacienne — En théorie des graphes, une matrice laplacienne, ou matrice de Laplace, est une matrice représentant un graphe. Définition La matrice laplacienne d un graphe G non orienté et non réflexif est définie par : Ml = Md − Ma où Md est la matrice… … Wikipédia en Français
log-laplacien, log-laplacienne ou log-normal, log-normale — ● log laplacien, log laplacienne ou log normal, log normale adjectif Loi log laplacienne ou log normale, Loi de probabilité d une variable aléatoire continue dont le logarithme suit une loi normale. ● log laplacien, log laplacienne ou log normal … Encyclopédie Universelle
Loi log-laplacienne ou log-normale — ● Loi log laplacienne ou log normale Loi de probabilité d une variable aléatoire continue dont le logarithme suit une loi normale … Encyclopédie Universelle
Théorie spectrale des graphes — La théorie spectrale des graphes s intéresse aux rapports entre le spectre d un graphe et ses propriétés, et fait partie de la théorie algébrique des graphes. Un graphe peut être représenté par plusieurs matrices, et les valeurs propres d une… … Wikipédia en Français
Théorie spectrale — des graphes La théorie spectrale des graphes s intéresse aux rapports entre le spectre d un graphe et ses propriétés, et fait partie de la théorie algébrique des graphes. Un graphe peut être représenté par plusieurs matrices, et les valeurs… … Wikipédia en Français
Théorème de Kirchhoff — Dans le domaine de la théorie des graphes, le théorème de Kirchhoff, aussi appelé matrix tree theorem, nommé d après le physicien Gustav Kirchhoff, est un théorème donnant le nombre exact d arbres couvrants pour un graphe quelconque. C est une… … Wikipédia en Français
Graphe (mathématiques) — Théorie des graphes Pour la notion mathématique utilisée en Théorie des ensembles, voir Graphe d une fonction. La théorie des graphes est une branche commune à l informatique et aux mathématiques étudiant les graphes et les objets qui lui… … Wikipédia en Français
Graphe (théorie des graphes) — Théorie des graphes Pour la notion mathématique utilisée en Théorie des ensembles, voir Graphe d une fonction. La théorie des graphes est une branche commune à l informatique et aux mathématiques étudiant les graphes et les objets qui lui… … Wikipédia en Français
Graphe partiel — Lexique de la théorie des graphes Article principal : Théorie des graphes. Sommaire : Haut A B C D E F G H I J K L M N O P Q R S T U V W X Y Z A … Wikipédia en Français