Théorème de Kirchhoff

Théorème de Kirchhoff: Dans le domaine de la théorie des graphes, le théorème de Kirchhoff, aussi appelé matrix-tree theorem, nommé d'après le physicien Gustav Kirchhoff, est un théorème donnant le nombre exact d'arbres couvrants pour un graphe quelconque. C'est une généralisation de la formule de Cayley qui donnait ce résultat pour les graphes complets.

Sommaire

1 Théorème de Kirchhoff

2 Un exemple

3 Remarques

4 Démonstration

4.1 Étape 1

4.2 Étape 2

4.3 Étape 3

5 Voir aussi

6 Références

Théorème de Kirchhoff

Le théorème de Kirchhoff s'appuie sur la notion de matrice laplacienne, définie elle-même comme la différence entre la matrice des degrés et la matrice d'adjacence du graphe.

Concrètement, pour un graphe $G = (V, E)$ où $V=\{v_1 ,\cdots ,v_n\}$ , la matrice laplacienne est définie par:

$(L)_{i,j}:=\left\{ \begin{matrix} \deg(v_i) & \mbox{si } i = j \\ -1 & \mbox{si } i \neq j \mbox{ et } (v_i,v_j) \in E \\ 0 & \mbox{sinon} \end{matrix} \right.$

Alors, le nombre $t (G)$ d'arbres couvrants du graphe $G$ est égal, au signe près, à la valeur de n'importe quel cofacteur de $L$ .

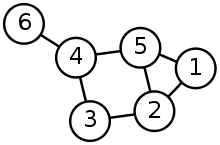
Un exemple

Ce graphe possède 11 arbres couvrants

On calcule d'abord la matrice laplacienne de ce graphe:
$L= \begin{pmatrix} 2 & -1 & 0 & 0 & -1 & 0\\ -1 & 3 & -1 & 0 & -1 & 0\\ 0 & -1 & 2 & -1 & 0 & 0\\ 0 & 0 & -1 & 3 & -1 & -1\\ -1 & -1 & 0 & -1 & 3 & 0\\ 0 & 0 & 0 & -1 & 0 & 1\\ \end{pmatrix}$
On supprime n'importe quelle ligne et n'importe quelle colonne de la matrice:
$L^*=\begin{pmatrix} 2 & -1 & 0 & -1 & 0\\ 0 & -1 & -1 & 0 & 0\\ 0 & 0 & 3 & -1 & -1\\ -1 & -1 & -1 & 3 & 0\\ 0 & 0 & -1 & 0 & 1\\ \end{pmatrix}$

Ainsi, $~~t(G)=\det(L^*)=11$ .

Remarques

Si le graphe de départ n'est pas connexe, alors la matrice laplacienne sera diagonale par bloc. En supprimant une ligne et une colonne, il y aura au moins une composante connexe pour laquelle aucune colonne n'aura été supprimée. La somme des colonnes de cette composante est alors nulle, donc tout cofacteur est nul. On retrouve bien le fait que seuls les graphes connexes ont des arbres couvrants.

Ce théorème permet de donner une démonstration rapide de la formule de Cayley. Cette dernière indique que le graphe complet $K n$ possède $n n - 2$ arbres couvrants. La matrice laplacienne est une matrice $n\times n$ de la forme:

$L_{n\times n}=\begin{pmatrix}n-1 & -1 & -1\\ -1 & \ddots & -1 \\ -1 & -1 & n-1 \\ \end{pmatrix}$
On peut par exemple supprimer la première ligne et la première colonne, on obtient donc une matrice $n-1 \times n-1$ de la forme:

$L^*_{n-1\times n-1}=\begin{pmatrix}n-1 & -1 & -1\\ -1 & \ddots & -1 \\ -1 & -1 & n-1 \\ \end{pmatrix}$
On effectue alors l'opération suivante: pour $i>1,~~C_i\leftarrow C_i -C_1$ :
$\det (L^*_{n-1\times n-1} )=\begin{vmatrix}n-1 & -n & -n & \cdots & -n & -n\\ -1 & n & 0 & \cdots & 0 & 0 \\ -1 & 0 & n & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ -1 & 0 & 0 & \cdots & n & 0\\ -1 & 0 & 0 & \cdots & 0 & n\\ \end{vmatrix}$
Puis, $L_1\leftarrow \sum_{i \geq 1}L_i$ :
$\det (L^*_{n-1\times n-1} )=\begin{vmatrix}1 & 0 & 0 & \cdots & 0 & 0\\ -1 & n & 0 & \cdots & 0 & 0 \\ -1 & 0 & n & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ -1 & 0 & 0 & \cdots & n & 0\\ -1 & 0 & 0 & \cdots & 0 & n\\ \end{vmatrix}$
Ainsi, en développant par rapport à la première ligne, on obtient le résultat.

Démonstration

Étape 1

Soit $D$ une orientation quelconque de $G$ , et $M$ la matrice d'incidence associée: si $G$ a $n$ nœuds et $m$ arêtes, alors $M$ est une matrice à $n$ lignes et $m$ colonnes dont le terme général est défini par:

$m_{i,j}:=\left\{ \begin{matrix} 1 & \mbox{si } v_i \mbox{ est la queue de } e_j \\ -1 & \mbox{si } v_i \mbox{ est la tête de } e_j \\ 0 & \mbox{si } v_i \notin e_j \end{matrix} \right.$

Calculons le terme général de $M * = M M t$ : il correspond au produit scalaire de deux lignes de $M$ . Si $i = j$ , alors $m^*_{i,j}$ compte $12$ pour des arêtes sortant de $v i$ et $( - 1) 2$ pour des arêtes arrivant à $v i$ , donc $m^*_{i,j}=deg(v_i)$ . Si $i\neq j$ , alors $m i, j = - 1$ si une arête relie $v i$ à $v j$ , indépendamment de la direction, et $0$ sinon.

On a donc: $L = M M t$

Étape 2

On ne considère que les graphes connexes, ce qui assure $m\geq n-1$ . On considère alors $B$ une sous matrice carrée $(n-1)\times (n-1)$ de $M$ .

Le sous graphe correspondant à $B$ contient donc $n$ nœuds et $n - 1$ arêtes, donc soit c'est un arbre couvrant, soit il contient un cycle. S'il contient un cycle, alors la somme des colonnes correspondantes dans $B$ sera nulle, et donc le déterminant de $B$ sera nul lui aussi.

S'il ne contient pas de cycle, c'est un arbre couvrant $T$ , qui contient au moins deux feuilles. $B$ a donc au moins une ligne correspondant à une feuille, donc une ligne contenant $n - 2$ termes nuls et un terme égal à $1$ ou $- 1$ . En développant le déterminant de $B$ par rapport à cette ligne, on obtient donc une relation de récurrence sur le nombre de nœuds $n$ du graphe. Si le graphe a un seul nœuds, $B$ est matrice vide de déterminant $1$ par convention, donc quelle que soit la valeur de $n$ , si $B$ représente un arbre couvrant $T$ , $\det(B) = \pm 1$ , et sinon, $det(B) = 0.$

Étape 3

On obtient $M *$ en supprimant une ligne quelconque de $M$ . Le déterminant de $M * (M *) t$ est donc un cofacteur de $L$ , au signe près. Par la Formule de Binet-Cauchy, on obtient: $\mbox{Cofacteur}(L)=\sum_{B\in \mathcal{H}} (\det(B))^2$

où $\mathcal{H}$ représente les sous-matrices $(n-1)\times (n-1)$ de $M *$ . D'après l'étape 2, les termes de la somme valent 1 pour chaque arbre couvrant, et 0 sinon, ce qui termine la démonstration.

Voir aussi

Théorie des graphes

Arbre couvrant

Références

Combinatorics and Graph Theory (Undergraduate Texts in Mathematics)- de John M. Harris, Jeffry L. Hirst, Michael J. Mossinghoff. Springer; 2nd ed. edition (September 19, 2008).

Portail des mathématiques

Catégorie :
Structure de données en théorie des graphes

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de Kirchhoff de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Theoreme de Tellegen — Théorème de Tellegen En électricité, le Théorème de Tellegen est une conséquence directe des lois de Kirchhoff qui traduit en particulier la conservation de l énergie dans un circuit électrique isolé. Ce théorème doit son nom à Bernard Tellegen,… … Wikipédia en Français
Théorème de tellegen — En électricité, le Théorème de Tellegen est une conséquence directe des lois de Kirchhoff qui traduit en particulier la conservation de l énergie dans un circuit électrique isolé. Ce théorème doit son nom à Bernard Tellegen, un chercheur… … Wikipédia en Français
Theoreme flot-max/coupe-min — Théorème flot max/coupe min Le théorème flot max/coupe min est un théorème de la théorie des graphes. Il généralise le théorème de König et le théorème de Hall (dans les graphes bipartis) et le théorème de Menger (dans les graphes quelconques).… … Wikipédia en Français
Théorème flot-max/coupe-min — Le théorème flot max/coupe min est un théorème de la théorie des graphes. Il généralise le théorème de König et le théorème de Hall (dans les graphes bipartis) et le théorème de Menger (dans les graphes quelconques). Il révèle que le calcul d une … Wikipédia en Français
Theoreme de Thevenin — Théorème de Thévenin Le théorème de Thévenin a été initialement découvert par le scientifique allemand Hermann von Helmholtz en 1853, puis en 1883 par l ingénieur télégraphe français Léon Charles Thévenin. Ce théorème est une propriété… … Wikipédia en Français
Théorème de thévenin — Le théorème de Thévenin a été initialement découvert par le scientifique allemand Hermann von Helmholtz en 1853, puis en 1883 par l ingénieur télégraphe français Léon Charles Thévenin. Ce théorème est une propriété électronique qui se déduit… … Wikipédia en Français
Theoreme de reciprocite — Théorème de réciprocité Le principe de réciprocité, que l on retrouve également dans d autres domaines de la physique, s exprime dans celui de l électricité grâce à une relation générale entre les courants et les tensions observés aux interfaces… … Wikipédia en Français
Theoreme de Millman — Théorème de Millman Le théorème de Millman est une forme particulière de la loi des nœuds exprimée en termes de potentiel. Il est ainsi nommé en l honneur de l électronicien américain Jacob Millman. Sommaire 1 Énonciation 2 Exemple 3 Applications … Wikipédia en Français
Theoreme de Norton — Théorème de Norton Le Théorème de Norton pour les réseaux électriques établit que tout circuit linéaire est équivalent à une source de courant idéale I, en parallèle avec une simple résistance R. Le théorème s applique à toutes les impédances,… … Wikipédia en Français
Théorème de millman — Le théorème de Millman est une forme particulière de la loi des nœuds exprimée en termes de potentiel. Il est ainsi nommé en l honneur de l électronicien américain Jacob Millman. Sommaire 1 Énonciation 2 Exemple 3 Applications … Wikipédia en Français

Mark and share
Search through all dictionaries
Translate…
Search Internet

Share the article and excerpts