Graphe partiel

Graphe partiel

Lexique de la théorie des graphes

Article principal : Théorie des graphes.
Sommaire : Haut - A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

A

  • Acyclique (graphe) : graphe ne contenant pas de cycle.
  • Adjacence (liste d') : structure de données constituée d'un tableau dont le ie élément correspond à la liste des voisins du ie sommet.
  • Adjacence (matrice d') : matrice d'éléments aij correspondant au nombre d'arêtes ayant pour extrémités les sommets d'indices i et j.
  • Adjacence (relation d') : propriété de deux sommets d'être connectés par la même arête (on parle de sommets adjacents) ou propriété de deux arêtes de présenter une extrémité commune (on parle d’arêtes adjacentes). Synonyme : relation de voisinage.
  • Adjoint (graphe) : synonyme de line graph.
  • Admittance : autre nom d'une matrice laplacienne.
  • Aléatoire (graphe) : un graphe est aléatoire, ou non déterministe, dès que sa construction fait intervenir des probabilités.
  • Arbre : graphe connexe sans cycle. Équivalent à : graphe connexe à n sommets et n − 1 arêtes.
  • Arc : arête dans un graphe orienté. Autre formulation : couple (ensemble ordonné de deux éléments) de sommets reliés par une arête dans un graphe non orienté.
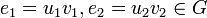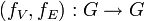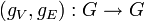  • Arc-transitif (graphe) : on dit qu'un graphe G est arc-transitif si son groupe d'automorphisme agit transitivement sur l'ensemble de ses arcs. Étant donné deux arêtes e_1 = u_1v_1, e_2 = u_2v_2 \in G, il existe deux automorphismes (f_V,f_E) : G \rightarrow G et (g_V,g_E) : G \rightarrow G tels que fE(e1) = e2, gE(e1) = e2, et fV(u1) = u2, fV(v1) = v2, gV(u1) = v2, gV(v1) = u2.
  • Arête : connexion entre deux sommets A et B. Dans le cas des graphes orientés on parle d'arc. Le terme « arête » est alors utilisé pour désigner l'ensemble des deux arcs (A,B), c'est-à-dire de A vers B, et (B,A), c'est-à-dire de B vers A.
  • Arête multiple : ensemble d'arêtes parallèles relatif à un couple de sommets.
  • Arête parallèle : arête ayant pour extrémités les mêmes sommets qu'une autre arête. On parle d'arêtes parallèles.
  • Arête-transitif (graphe) : on dit qu'un graphe est arête-transitif si son groupe d'automorphisme agit transitivement sur l'ensemble de ses arêtes. Autre formulation de la condition : pour tout couple d'arêtes, au moins un automorphisme envoie la première composante sur la seconde. Toutes les arêtes jouent exactement le même rôle à l'intérieur du graphe. Exemple : un graphe complet.
  • Automorphisme : isomorphisme d'un graphe sur lui-même. Chaque graphe possède au moins un automorphisme : l'identité. L'ensemble des automorphismes d'un graphe forme un groupe.

B

  • Biparti : un graphe est dit biparti s'il existe une partition de son ensemble de sommets en deux sous-ensembles U et V telle que deux sommets adjacents soient dans deux parties différentes. Cela revient à dire que le graphe est 2-coloriable.
  • Biparti complet : un graphe est dit biparti complet s'il est biparti et qu'il existe une arête entre chaque sommet de U et de V. On note Km,n le graphe biparti complet tel que | U | = m et | V | = n.
  • Boucle : arête partant d'un sommet et arrivant sur lui-même.

C

  • Chemin : soit un graphe G = (V,E). Un chemin P = (S,A) est défini par S = {s0,...,sk}, A = {s0s1,...,sk − 1sk}, 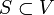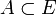S \subset V, A \subset E. Autrement dit, un chemin est une suite consécutive d'arcs dans un graphe non orienté. Dans le cas d'un graphe orienté, ou d'une suite d'arêtes dans un graphe non orienté, on parle de chaîne. Une définition alternative est celle d'un arbre à deux feuilles (les deux extrémités de la chaîne). La longueur d'un chemin est son nombre d'arêtes, c'est-à-dire |A|. Un chemin est dit élémentaire s'il ne repasse pas par un sommet. On considère en général implicitement le cas de chemins élémentaires.
  • Circonférence : longueur du plus grand cycle.
  • Clique : sous-graphe induit complet, c'est-à-dire un sous-ensemble des sommets tels que chacun est connecté à tous les autres. Il s'agit aussi du complémentaire d'un ensemble indépendant (ou stable).
  • Coloration : fonction associant à tout sommet une couleur, tels que deux sommets adjacents aient une couleur différente (c'est-à-dire partitionne les sommets en ensembles indépendants). Le nombre minimum de couleurs pour un graphe G est le nombre chromatique dénoté χ(G).
  • k-coloration : coloration d'un graphe en k couleurs distinctes.
  • Complémentaire : le complémentaire (ou inverse, ou complément) 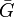\bar{G} d'un graphe G = (V,E) est un graphe qui a les mêmes sommets que G, reliés si et seulement s’ils ne sont pas reliés dans le graphe d'origine, soit \bar{G} = (V, [V]^2 \backslash E).
  • Complet : dans un graphe complet chaque sommet est relié à tous les autres. On note Kn le graphe complet à n sommets.
  • Composante : un composante d'un graphe est un sous-graphe connexe maximal.
  • Connexe : un graphe est connexe s'il existe un chemin entre tout couple de sommets. Quand on parle de connexité pour un graphe orienté, on considère non pas ce graphe mais le graphe non-orienté correspondant. On peut déterminer ceci par exemple avec un algorithme de parcours en profondeur. Un graphe orienté est dit fortement connexe si, pour tout couple de sommets (u,v) du graphe, il existe un chemin de u à v et de v à u.
  • k-connexe : un graphe est k-connexe s'il cesse d'être connexe uniquement quand on supprime k arêtes; ceci peut se vérifier par la présence de k chaînes disjointes (ne partageant aucune arête) entre chaque sommet.
  • Contenir : on dit d'un graphe G qu'il contient H si H est un sous-graphe induit de G.
  • Contraction : supprime une arête d'un graphe en fusionnant ses deux extrémités. Autrement dit, la contraction G / e d'une arête exy à un sommet x rend le sommet x adjacent à tous les voisins précédents de y.
  • Cospectral : deux graphes sont cospectraux s'ils ont le même spectre. Ce spectre pouvant être basé sur plusieurs matrices, on peut préciser A-cospectraux pour le spectre de la matrice d'adjacence et L-cospectraux pour le spectre de la matrice laplacienne.
  • Cubique : graphe 3-régulier.
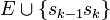  • Cycle : chemin dont les sommets de départ et de fin sont les mêmes. Autrement dit, soit un chemin dont les arêtes sont E = {s0s1,...,sk − 2sk − 1} : le cycle est alors défini par E \cup \{s_{k-1}s_k\}.
  • Cyclomatique : le nombre cyclomatique d'un graphe G = (V,E) est M = | E | − | V | + P, où P est le nombre de composantes connexes. C'est également la dimension de l'espace des cycles.
Sommaire : Haut - A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

D

  • Degré : dans le cas non-orienté, le degré d(s) du sommet s est le nombre d'arêtes de s. Dans le cas d'un graphe orienté, le degré entrant d + (s) est le nombre d'arcs vers s tandis que le degré sortant d − (s) est le nombre d'arcs sortant de s. Le degré maximum est noté Δ(G), et le degré minimal δ(G). Dans la matrice des degrés, l'entrée Dii est le degré du sommet i.
  • Diamètre : excentricité maximale des sommets, notée D.
  • Dilatation : dans un plongement où f associe des sommets d'un graphe G à ceux d'un graphe H, la dilatation est la distance maximale entre les images par f de deux sommets adjacents dans G. Autrement dit, si deux sommets sont voisins dans un graphe, leurs images peuvent être séparées par un chemin qui augmente donc la distance entre eux, et la plus grande augmentation est la dilatation.
  • Distance : la distance dG(x,y) entre x et y est la longueur du plus court chemin entre ces sommets; aussi appelée distance géodésique.
  • Distance-régulier : un graphe est distance-régulier si pour tous sommets 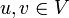u, v \in V, le nombre de sommets voisins de u à distance i et le nombre de sommets voisins de v à distance j ne dépendent que de i,j et de la distance d(u,v) entre u et v. Formellement, 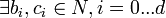\exists b_i, c_i \in N, i = 0...d tels que c0 = 0 et
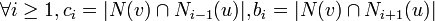
    \forall i \ge 1, c_i = |N(v) \cap N_{i-1}(u)|, b_i = |N(v) \cap N_{i+1}(u)|
  • Dominant (ou absorbant) : un ensemble de sommet est dominant si tout sommet en fait partie ou est voisin d'un sommet en faisant partie.

E

  • Espace : soit un graphe G = (V,E). L'espace des sommets est l'espace vectoriel sur {0,1} avec comme base {v1,...,vn}, soit un espace de dimension n. De même, l'espace des arêtes est l'espace vectoriel sur {0,1} avec comme base {e1,...,em}, soit un espace de dimension m. Le principe du 0 est du 1 est qu'on obtient 1 pour un sommet (ou arête) appartenant à l'espace et 0 sinon.
  • Étiquetage : fonction associant chaque sommet à une étiquette, pouvant être dans n'importe quel ensemble (réels, mots, couleurs...).
  • Eulérien : un chemin eulérien est un chemin qui passe par toutes les arêtes exactement une fois. Un cycle eulérien est un chemin eulérien où les sommets de départ et d'arrivés sont les mêmes. Un graphe où l'on peut construire un cycle eulérien est appelé graphe eulérien; si l'on ne peut construire que des chemins eulériens, alors le graphe est semi-eulérien. Un graphe est eulérien si chaque sommet est de degré pair.
  • Excentricité : l'excentricité d'un sommet est sa distance maximale à tous les autres sommets.
  • Expansion : si H est un mineur de G (i.e. H résulte d'une série de contractions) alors G est une expansion de H. Une opération d'expansion remplace un sommet s par deux sommets s1,s2 connectés par une arête, et s1 et s2 sont connectés à tous les voisins de s. 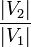Dans le cas d'un plongement d'un graphe G1 = (V1,E1) dans G2 = (V2,E2), une expansion a une autre signification : il s'agit du rapport entre la taille des deux graphes, soit \frac{|V_2|}{|V_1|}.
  • Extra-planaire : voir outer-planar.

F

  • Facteur : un k-facteur est un sous-graphe couvrant k-régulier.
  • Feuille (dans un arbre) : sommet de degré 1.
  • Fini (graphe) : un graphe est dit fini si le nombre de ses arêtes et de ses sommets est fini. Un graphe infini dont chaque sommet a un degré fini est dit localement fini.
  • Forêt : graphe acyclique. Chaque composante connexe d'une forêt forme un arbre.

G

H

  • Hamiltonien : un graphe est hamiltonien s'il a au moins un cycle passant par tous les sommets exactement une fois, et ce cycle est appelé cycle hamiltonien. Un cycle hamiltonien est aussi un cycle élémentaire de même ordre que le graphe.
  • Hypergraphe : généralise la notion de graphe en autorisant une arête à relier plus de deux sommets.
Sommaire : Haut - A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

I

  • Incidence (matrice) : La matrice d'incidence d'un graphe G = (V,E) est la matrice de dimensions | V | x | E | dans laquelle l'entrée bij vaut 1 si le sommet vi est une extrémité de l'arête xj, 2 si xj est une boucle sur vi et 0 sinon. Dans le cas orienté, on a bij = − 1 si xj sort de vi et 1 si elle y rentre.
  • Indépendant : deux sommets sont indépendants s'ils ne sont pas connectés, c'est-à-dire pas adjacents. Un ensemble de sommets est indépendant (ou stable) s'il n'y a pas deux de ses sommets adjacents.
  • Infini : contraire de fini.
  • Intervalles : un graphe d'intervalles est un graphe G tel que l'on puisse associer à chacun de ses sommet un intervalle sur l'ensemble des réels et tel que pour chaque sommet u et v de G il y a une arête entre u et v si et seulement si l'intersection entre leurs intervalles associés n'est pas nulle,
  • Invariant : Propriété du graphe dépendant uniquement de sa structure (i.e. indépendante de son étiquetage). Par exemple, le degré moyen du graphe ou son spectre.
  • Isolé : sommet de degré 0, c'est-à-dire n'ayant pas de voisin.
  • Isomorphisme : un isomorphisme de graphe est un morphisme de graphe bijectif (ou inversible).
  • Isomorphe : deux graphes sont isomorphes s'il existe un isomorphisme de graphe de l'un vers l'autre. C'est-à-dire s'ils ont exactement la même structure. Il suffit de remplacer les étiquettes des sommets pour qu'un graphe soit la copie conforme de l'autre.
  • Isospectral : voir cospectral.

J

  • Jumeau : deux sommets sont jumeaux s'ils ont le même voisinage. Des vrais jumeaux respectent en plus la contrainte d'être voisins l'un de l'autre, et si cette contrainte n'est pas respectée alors on parle de faux jumeaux. 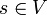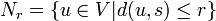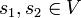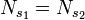La notion de voisinage peut-être généralisée[1] pour une distance supérieure à 1 : on défini le voisinage de s \in V jusqu'à distance r par N_r = \{u \in V | d(u,s) \le r\}, et deux jumeaux s_1, s_2 \in V ont alors N_{s_1} = N_{s_2}.

K

L

  • Laplacienne (matrice) : matrice L = D − A où D est la matrice des degrés et A la matrice d'adjacence; on obtient sa forme normalisée L' par L' = D − 1 / 2LD − 1 / 2 = I − D − 1 / 2AD − 1 / 2, où I dénote la matrice identité. Est utilisée dans la théorie spectrale des graphes.
  • Libre d'échelle : un graphe est libre d'échelle si la distribution de ses degrés est proche d'une loi de puissance. Cette notion provient de la physique, et les divergences locales ou l'écart de la distribution par rapport à une loi de puissance ne sont pas spécifiés.
  • Line graph : le line graph d'un graphe G est le graphe L(G) où on inverse sommets et arêtes, c'est-à-dire que deux sommets adjacents dans le line graph correspondent à deux arêtes incidentes à un même sommet dans G.

M

  • Maille (ou girth en anglais) : longueur du plus court cycle. Si un graphe est acyclique, sa maille est considérée comme infinie. La maille paire (respectivement maille impaire) est la longueur du plus court cycle de longueur paire (respectivement impaire).
  • Mineur : un graphe H est un mineur de G s'il est isomorphe à un graphe pouvant être obtenu en contractant zéro ou plus arêtes de G.
  • Morphisme : application entre deux graphes qui respecte la structure de ces graphes.
  • Multigraphe : un graphe doté d'une ou plusieurs arêtes multiples.

N

  • Noeud : terminologie utilisée dans les réseaux pour un sommet. Un noeud interne est un sommet dans un arbre de degré supérieure à 1, c'est-à-dire n'étant pas une feuille.
  • Noyau : sous-ensemble de sommets à la fois stable et dominant.

O

  • Ordre : nombre de sommets du graphe.
  • Orienté : un graphe est orienté si les arêtes ont un sens, par exemple euv indique qu'il y a un arc de u à v. Un graphe est non-orienté si ses arêtes n'ont pas de sens  : euv indique qu'il y a une arête entre u et v.
  • Outer-planar : dans un graphe planaire, on considère les régions (ou faces) entourées par des arêtes comme internes. L'ensemble du graphe est donc entouré par une région externe. Si toutes les faces internes sont adjacentes à la face externe, alors le graphe est outer-planar.
Sommaire : Haut - A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

P

  • Parfait : un graphe est parfait si le nombre chromatique de chacun de ses sous-graphes induits H est égal à la taille de la clique maximale de H.
  • Partition : séparation des graphes du sommets en des ensembles disjoints de sommets dont l'union permet de retrouver tous les sommets. Formellement, une partition sépare V en 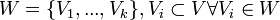W = \{V_1, ..., V_k\}, V_i \subset V \forall V_i \in W tel que 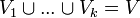V_1 \cup ... \cup V_k = V et \forall V_i, V_j \in W, V_i \cap V_j = \emptyset.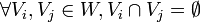
  • Petit monde : un graphe a le phénomène du petit-monde si son coefficient de clustering est élevé et la distance moyenne entre deux sommets faible. Cette notion provient de la physique, et il n'y a pas de définition exacte quant à ce qui est élevé et ce qui est faible; on considère la distance moyenne comme faible tant qu'elle n'excède pas le logarithme du nombre de sommets.
  • Planaire : un graphe est planaire si on peut le dessiner dans un plan sans croiser deux arêtes. Un graphe est planaire s'il ne contient pas K5 et K3,3 comme mineurs.
  • Plongement : soient deux graphes G1 = (V1,E1),G2 = (V2,E2). Un plongement est une fonction injective de V2 dans V1 tel que chaque arête de V2 corresponde à un chemin disjoint de G1. Un plongement permet de dire qu'on peut utiliser un graphe pour simuler les capacités de l'autre en termes de connexion : s'il y a une arête (i.e. un chemin dédié) entre deux sommets, alors on la retrouvera dans le graphe simulant sous la forme d'un chemin dédié (mais pouvant être plus long).
  • Polynôme caractéristique : le polynôme | λI − A | de la matrice d'adjacence A d'un graphe G est son polynôme caractéristique, et on le note PG(λ).
  • Pondéré : un graphe pondéré est celui auquel on applique une fonction de valuation.
  • Promenade (ou parcours) : voir chemin (considéré en général comme non-élémentaire). Une promenade close (ou parcours fermé) est un cycle.
  • Puits : dans un problème de flot, sommet consommant le flot. Généralement de degré sortant nul, mais pas nécessairement.

Q

R

  • Régulier : un graphe est k-régulier si chacun de ses sommets est de degré k.
  • Relation de Djokovìc-Winkler : deux arêtes exy et euv sont en relation de Djokovìc-Winkler, et on le note exyΘeuv si on a l'inégalité 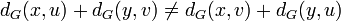d_G(x,u) + d_G(y,v) \neq d_G(x,v) + d_G(y,u). Cette relation est réflexive et symétrique[2].

S

  • Simple (ou Schlicht[3]) : graphe fini, non orienté, sans boucles ni arêtes multiples.
  • Sommet-transitif : on dit qu'un graphe est sommet-transitif si son groupe d'automorphisme agit transitivement sur l'ensemble de ses sommets. Autre formulation de la condition : pour tout couple de sommets, au moins un automorphisme envoie la première composante sur la seconde. Tous les sommets jouent exactement le même rôle à l'intérieur du graphe. Un graphe sommet-transitif est ainsi nécessairement régulier.
  • Source (dans un problème de flot) : sommet produisant le flot. Un tel sommet est généralement de degré entrant nul, mais pas nécessairement.
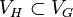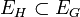  • Sous-graphe : graphe contenu dans un autre graphe. Formellement, avec des notations intuitives, un graphe H = (VH,EH est un sous-graphe de G = (VG,EG) si V_H \subset V_G et E_H \subset E_G.
    H est un sous-graphe couvrant ou graphe partiel de G (i.e. H couvre G) si, en plus, tous les sommets de G sont dans H (VH = VG).
    H est un sous-graphe induit de G si, pour tout couple (x,y) de sommets de H, x est connecté à y dans H si et seulement si x est connecté à y dans G. Autre formulation de la condition : l'ensemble des arêtes de H correspond à l'ensemble des arêtes de G incidentes à deux sommets de H.
  • Spanner : sous-graphe couvrant dont on essaye de minimiser le nombre d'arêtes (i.e. la densité) tout en conservant des bonnes propriétés de distance. Dans un spanner additif (respectivement multiplicatif), la distance entre deux sommets peut être augmentée (respectivement multipliée) jusqu'à un certain facteur appelé le délai (respectivement la dilatation).
  • Spectre : ensemble des valeurs propres d'une matrice représentant le graphe. La matrice peut être de Laplace ou d'adjacence. Les relations entre le spectre du graphe et ses propriétés font l'objet de la théorie spectrale des graphes.
  • Stable (ensemble) : ensemble de sommets 2 à 2 indépendants. Synonyme : ensemble indépendant.
  • Subdivision : la subdivision d'un graphe consiste à ajouter des sommets sur les arêtes, c'est-à-dire à remplacer des arêtes par des chemins. En particulier S(G) est le graphe où chaque arête de G a été remplacée par un chemin de longueur deux par insertion d'un sommet dans chaque arête.
  • Symétrique : un graphe est symétrique s'il est à la fois arête-transitif et sommet-transitif. Cela revient à vérifier que toutes ses arêtes et tous ses sommets sont indistinguables en termes d'isomorphisme de graphe. Exemple : graphe de Petersen.

T

  • Technique spectrale : technique faisant intervenir le spectre du graphe.
  • Transversal : un transversal (ou couverture nodale, ou support) d'un graphe est un sous-ensemble de sommet T tel que toute arête du graphe est incidente à au-moins un sommet de T. Le complémentaire d'un transversal est un stable.
  • Triangle : cycle de longueur trois.
  • Triangulé : un graphe est triangulé s'il ne contient pas un cycle de longueur quatre sans corde comme mineur. Les arbres, et les graphes d'intervalles notamment, sont triangulés.
  • Trivial : un graphe est trivial s'il a un seul ou aucun sommet. On peut utiliser un graphe trivial pour commencer une preuve par récurrence, mais ils sont implicitement exclus des théorèmes dont ils constitueraient parfois des contre-exemples inintéressants.
Sommaire : Haut - A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

U

V

  • Valuation : fonction associant un poids à chaque arête.
  • Vecteur d'intersection : séquence {b0,b1,...bD,c1,c2,...,cD} d'un graphe distance-régulier.

W

X

Y

Z


Références pour la terminologie non-standard
  1. ↑ (en) Irène Charon, Iiro Honkala, Olivier Hudry et Antoine Lobstein - Structural properties of twin-free graphs, The electronic journal of combinatorics, volume 14, 2007.
  2. ↑ (en) D. Djokovìc - Distance preserving subgraphs of hypercubes, Journal of Combin. Theory. Ser. B, numéro 14, pages 263-267, 1973.
  3. ↑ (en)Dragos M. Cvetkovic et Michael Doob et Horst Sachs - Spectra of Graphs, Heidelberg, Leipzig, 1994, (ISBN 3335004078).



  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Lexique de la th%C3%A9orie des graphes ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Graphe partiel de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Lexique (graphe) — Lexique de la théorie des graphes Article principal : Théorie des graphes. Sommaire : Haut A B C D E F G H I J K L M N O P Q R S T U V W X Y Z A …   Wikipédia en Français

  • Sous-graphe — En théorie des graphes, un sous graphe est un graphe contenu dans un autre graphe. Formellement, un graphe H = (VH,EH) est un sous graphe de G = (VG,EG) si et . L ensemble des sommets du sous graphe H est un sous ensemble de l ensemble des… …   Wikipédia en Français

  • Ordre partiel — Relation d ordre Une relation d’ordre dans un ensemble E est une relation binaire dans cet ensemble qui permet de comparer ses éléments entre eux de manière cohérente. Un ensemble muni d’une relation d’ordre est un ensemble ordonné ou tout… …   Wikipédia en Français

  • Hypergraphe — Exemple d hypergraphe : V = {v1,v2,v3,v4,v5,v6,v7}, E = {e1,e2,e3,e4} = {{v1,v2,v3},{v2,v3}, {v3,v …   Wikipédia en Français

  • Hypergraphes — Hypergraphe Exemple d hypergraphe: V = {v1,v2,v3,v4,v5,v6,v7}, E = {e1,e2,e3,e4} = {{v1,v2,v3},{v2,v3}, {v3,v5,v6},{v4}}. Les hyperg …   Wikipédia en Français

  • Lexique de la théorie des graphes — Article principal : Théorie des graphes. Sommaire : Haut A B C D E F G H I J K L M N O P Q R S T U V W X Y Z A Acyclique (grap …   Wikipédia en Français

  • Lexique De La Théorie Des Graphes — Article principal : Théorie des graphes. Sommaire : Haut A B C D E F G H I J K L M N O P Q R S T U V W X Y Z A …   Wikipédia en Français

  • Lexique de la theorie des graphes — Lexique de la théorie des graphes Article principal : Théorie des graphes. Sommaire : Haut A B C D E F G H I J K L M N O P Q R S T U V W X Y Z A …   Wikipédia en Français

  • Lexique en théorie des graphes — Lexique de la théorie des graphes Article principal : Théorie des graphes. Sommaire : Haut A B C D E F G H I J K L M N O P Q R S T U V W X Y Z A …   Wikipédia en Français

  • Théorème de Robertson-Seymour — En mathématiques, et plus précisément en théorie des graphes, le théorème de Robertson–Seymour (parfois également appelé le théorème des mineurs, et connu, avant qu il soit démontré, sous le nom de conjecture de Wagner), est un théorème démontré… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”