Laplacien vectoriel

Opérateur laplacien vectoriel

Articles d'analyse vectorielle

Objets d'étude
Champ vectoriel	Champ scalaire
Équation aux dérivées partielles
de Laplace	de Poisson
Opérateurs
Nabla	Gradient
Rotationnel	Divergence
Laplacien scalaire	Bilaplacien
Laplacien vectoriel	D'alembertien
Théorèmes
de Green	de Stokes
de Helmholtz	de flux-divergence
du gradient	du rotationnel

En analyse vectorielle, le laplacien vectoriel est un opérateur différentiel pour les champs vectoriels. Il présente beaucoup de similitudes avec l'opérateur laplacien scalaire.

Sommaire

1 Définitions
2 Expressions dans d'autres systèmes de coordonnées
- 2.1 Coordonnéees cylindriques
- 2.2 Coordonnées sphériques
3 Applications
4 Voir aussi

Définitions

Dans un espace euclidien, le laplacien vectoriel se définit le plus simplement en se plaçant dans un système de coordonnées cartésiennes. Dans ce cas, les composantes du laplacien vectoriel d'un champ de vecteurs quelconque A a pour composantes le laplacien des composantes de A. En d'autres termes, dans un espace à trois dimensions, si l'on écrit

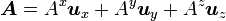$\boldsymbol A = A^x \boldsymbol u_x + A^y \boldsymbol u_y + A^z \boldsymbol u_z$ ,

alors le laplacien vectoriel de A s'écrit

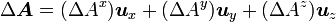$\Delta \boldsymbol A = (\Delta A^x) \boldsymbol u_x + (\Delta A^y) \boldsymbol u_y + (\Delta A^z) \boldsymbol u_z$ .

Expressions dans d'autres systèmes de coordonnées

À partir de l'expression en coordonnées cartésiennes, on peut exprimer le laplacien dans tout autre système de coordonnées, puisqu'une fois le nouveau système de coordonnées défini, on peut exprimer les vecteur de la nouvelle base en fonction de deux de la base cartésienne, tout comme on peut exprimer les dérivées partielles par rapport aux nouvelles coordonnées en fonction des dérivées partielles par rapport aux coordonnées cartésiennes. À trois dimensions, un méthode alternative (mais guère plus rapide) consiste à utiliser la formule du rotationnel du rotationnel, qui s'écrit pour tout champ de vecteurs :

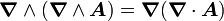$\boldsymbol \nabla \wedge (\boldsymbol \nabla \wedge \boldsymbol A) = \boldsymbol \nabla (\boldsymbol \nabla \cdot \boldsymbol A)$ .

On obtient ainsi les formules suivantes :

Coordonnéees cylindriques

Dans le système de coordonnées cylindriques usuel ρ, θ, z, on a :

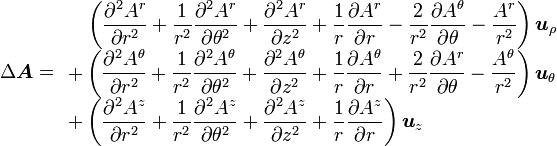$\Delta \boldsymbol A = \begin{array}{l} \displaystyle\quad \left(\frac{\partial^2 A^r}{\partial r^2} + \frac{1}{r^2} \frac{\partial^2 A^r}{\partial \theta^2} + \frac{\partial^2 A^r}{\partial z^2} + \frac{1}{r} \frac{\partial A^r}{\partial r} - \frac{2}{r^2} \frac{\partial A^\theta}{\partial \theta} - \frac{A^r}{r^2}\right) \boldsymbol u_\rho \\ \displaystyle + \left(\frac{\partial^2 A^\theta}{\partial r^2} + \frac{1}{r^2} \frac{\partial^2 A^\theta}{\partial \theta^2} + \frac{\partial^2 A^\theta}{\partial z^2} + \frac{1}{r} \frac{\partial A^\theta}{\partial r} + \frac{2}{r^2} \frac{\partial A^r}{\partial \theta} - \frac{A^\theta}{r^2}\right)\boldsymbol u_\theta \\ \displaystyle + \left(\frac{\partial^2 A^z}{\partial r^2} + \frac{1}{r^2} \frac{\partial^2 A^z}{\partial \theta^2} + \frac{\partial^2 A^z}{\partial z^2} + \frac{1}{r} \frac{\partial A^z}{\partial r}\right)\boldsymbol u_z \end{array}$ .

Coordonnées sphériques

Dans le système de coordonnées sphériques usuel r, θ, φ, on a :

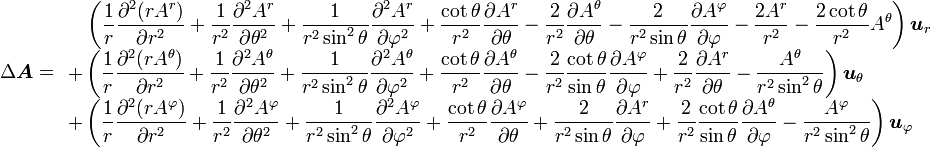$\Delta \boldsymbol A = \begin{array}{l} \displaystyle \quad\left(\frac{1}{r} \frac{\partial^2 (r A^r)}{\partial r^2} + \frac{1}{r^2} \frac{\partial^2 A^r}{\partial \theta^2} + \frac{1}{r^2 \sin^2 \theta} \frac{\partial^2 A^r}{\partial \varphi^2} + \frac{\cot \theta}{r^2} \frac{\partial A^r}{\partial \theta} - \frac{2}{r^2} \frac{\partial A^\theta}{\partial \theta} - \frac{2}{r^2 \sin \theta} \frac{\partial A^\varphi}{\partial \varphi} - \frac{2A^r}{r^2} - \frac{2 \cot \theta}{r^2} A^\theta \right)\boldsymbol u_r \\ \displaystyle + \left(\frac{1}{r} \frac{\partial^2 (r A^\theta)}{\partial r^2} + \frac{1}{r^2} \frac{\partial^2 A^\theta}{\partial \theta^2} + \frac{1}{r^2 \sin^2 \theta} \frac{\partial^2 A^\theta}{\partial \varphi^2} + \frac{\cot \theta}{r^2} \frac{\partial A^\theta}{\partial \theta} - \frac{2}{r^2} \frac{\cot \theta}{\sin \theta} \frac{\partial A^\varphi}{\partial \varphi} + \frac{2}{r^2} \frac{\partial A^r}{\partial \theta} - \frac{A^\theta}{r^2 \sin^2 \theta} \right)\boldsymbol u_\theta \\ \displaystyle +\left(\frac{1}{r} \frac{\partial^2 (r A^\varphi)}{\partial r^2} + \frac{1}{r^2} \frac{\partial^2 A^\varphi}{\partial \theta^2} + \frac{1}{r^2 \sin^2 \theta} \frac{\partial^2 A^\varphi}{\partial \varphi^2} + \frac{\cot \theta}{r^2} \frac{\partial A^\varphi}{\partial \theta} + \frac{2}{r^2 \sin \theta} \frac{\partial A^r}{\partial \varphi} + \frac{2}{r^2} \frac{\cot \theta}{\sin \theta} \frac{\partial A^\theta}{\partial \varphi} - \frac{A^\varphi}{r^2 \sin^2 \theta} \right)\boldsymbol u_\varphi \end{array}$ .

Applications

Le laplacien vectoriel est présent en particulier :

en électromagnétisme ;
en mécanique des fluides visqueux où il apparait dans les équations de Navier-Stokes ;
dans la formule du rotationnel du rotationnel (qui est à l'origine de son irruption en électromagnétisme).

Voir aussi

Portail des mathématiques
Portail de la physique

Ce document provient de « Op%C3%A9rateur laplacien vectoriel ».

Catégorie : Analyse vectorielle

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Laplacien vectoriel de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Operateur laplacien vectoriel — Opérateur laplacien vectoriel Articles d analyse vectorielle … Wikipédia en Français
Opérateur Laplacien vectoriel — Articles d analyse vectorielle … Wikipédia en Français
Opérateur laplacien vectoriel — En analyse vectorielle, le laplacien vectoriel est un opérateur différentiel pour les champs vectoriels. Il présente beaucoup de similitudes avec l opérateur laplacien scalaire. Sommaire 1 Définitions 2 Expressions dans d autres systèmes de… … Wikipédia en Français
Laplacien Discret — Articles d analyse vectorielle Objets … Wikipédia en Français
Laplacien — Opérateur laplacien Articles d analyse vectorielle Objet … Wikipédia en Français
Laplacien (signification physique) — Opérateur laplacien Articles d analyse vectorielle Objet … Wikipédia en Français
Laplacien scalaire — Opérateur laplacien Articles d analyse vectorielle Objet … Wikipédia en Français
Laplacien discret — Soit une fonction réelle f de deux variables réelles {x, y}; on appelle, en analyse numérique, laplacien discret de f la dérivée seconde discrète selon x + celle selon y, soit : Cela est souvent utilisé pour résoudre des problèmes de… … Wikipédia en Français
Calcul vectoriel — Analyse vectorielle Articles d analyse vectorielle … Wikipédia en Français
Operateur laplacien — Opérateur laplacien Articles d analyse vectorielle Objet … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Laplacien vectoriel

Opérateur laplacien vectoriel

Sommaire

Définitions