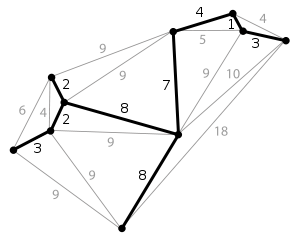
- Arbre couvrant
-
Arbre couvrant de poids minimal
L'arbre couvrant de poids minimal d'un graphe planaire. Chaque arête est identifiée avec son poids qui, ici, est approximativement sa longueur.
Étant donné un graphe non orienté et connexe, un arbre couvrant de ce graphe est un sous-ensemble qui est un arbre et qui connecte tous les sommets ensemble.
Un graphe peut comporter plusieurs arbres couvrants différents. On peut associer un poids à chaque arête, ce qui est un nombre qui représente le coût de cette arête, et prendre la somme des poids des arêtes de l'arbre couvrant. Un arbre couvrant de poids minimal est un arbre couvrant dont le poids est plus petit ou égal à celui de tous les autres arbres couvrants du graphe.
Un graphe non orienté et général possède une forêt couvrante de poids minimal.
Un problème connu utilisant l'arbre du poids minimal est le suivant :
- On génère n points aléatoirement dans un carré de coté 1
- On génère le graphe complet dont les sommets sont les points générés
- On résout le problème de l'arbre de poids minimal
- On calcule Ln le poids total de l'arbre
Ce poids est asymptotiquement égal à
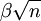avec β = 0.658...
L'arbre couvrant de poids minimal est aussi connu sous certains autres noms, tel qu'arbre couvrant minimum ou encore arbre sous-tendant minimum.Références
- (en) Otakar Boruvka on Minimum Spanning Tree Problem (translation of the both 1926 papers, comments, history) (2000) Jaroslav Nesetril, Eva Milková, Helena Nesetrilová (Section 7 gives his algorithm, which looks like a cross between Prim's and Kruskal's.)
- (en) A Minimum Spanning Tree Algorithm with Inverse-Ackermann Type Complexity, Bernard Chazelle, 1999.
- [1]
- (en) Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Chapter 23: Minimum Spanning Trees, pp.561–579.
Voir aussi
- Algorithme de Prim
- Algorithme de Kruskal
- Algorithme de Borůvka
- Algorithme de Dijkstra
Lien externe
Catégories : Arbre (structure de données) | Arbre (graphe)
Wikimedia Foundation. 2010.
